目录
一、按摩师
二、打家劫舍
三、删除并获得点数
四、粉刷房子
五、买卖股票的最佳时机
六、买卖股票的最佳时机(含手续费)
七、买卖股票的最佳时机III
八、买卖股票的最佳时机IV
一、按摩师

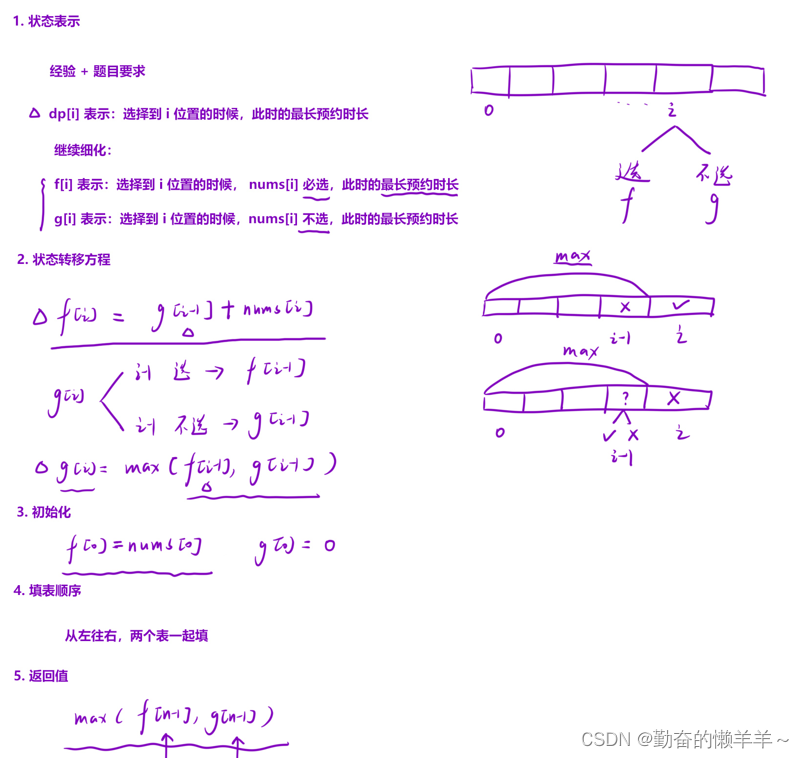
class Solution { public: int massage(vector<int>& nums) { int n =nums.size(); if(n == 0) return 0; vector<int> f(n); auto g = f; f[0] = nums[0]; for(int i = 1;i < n;i++){ f[i] = g[i-1] + nums[i]; g[i] = max(f[i-1],g[i-1]); } return max(f[n-1],g[n-1]); } };
二、打家劫舍


class Solution {
public:
int rob1(vector<int>& nums,int l,int r) {
if(l>r) return 0;
int n =nums.size();
if(n == 0) return 0;
vector<int> f(n);
auto g = f;
f[l] = nums[l];
for(int i = l;i <= r;i++){
f[i] = g[i-1] + nums[i];
g[i] = max(f[i-1],g[i-1]);
}
return max(f[r],g[r]);
}
int rob(vector<int>& nums) {
int n = nums.size();
int ret1 = rob1(nums,2,n-2)+nums[0];
int ret2 = rob1(nums,1,n-1);
return max(ret1,ret2);
}
};三、删除并获得点数

class Solution {
public:
int deleteAndEarn(vector<int>& nums) {
int n = nums.size();
const int N = 10001;
int arr[N] = {0};
for(auto e : nums)
{
arr[e] += e;
}
vector<int> f(N);
auto g = f;
for(int i = 1;i < N;i++){
f[i] = g[i-1] + arr[i];
g[i] = max(f[i-1],g[i-1]);
}
return max(f[N-1],g[N-1]);
}
};四、粉刷房子



class Solution {
public:
int minCost(vector<vector<int>>& costs) {
int n = costs.size();
vector<vector<int>> dp(n+1,vector<int>(3));
for(int i = 1;i <= n;i++)
{
dp[i][0] = costs[i-1][0] + min(dp[i-1][1],dp[i-1][2]);
dp[i][1] = costs[i-1][1] + min(dp[i-1][0],dp[i-1][2]);
dp[i][2] = costs[i-1][2] + min(dp[i-1][0],dp[i-1][1]);
}
return min(dp[n][0],min(dp[n][1],dp[n][2]));
}
};五、买卖股票的最佳时机




class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n,vector<int>(3));
dp[0][0] = -prices[0];
for(int i = 1;i < n;i++){
dp[i][0] = max(dp[i-1][0],dp[i-1][1] - prices[i]);
dp[i][1] = max(dp[i-1][1],dp[i-1][2]);
dp[i][2] = dp[i-1][0]+prices[i];
}
return max(dp[n-1][1],dp[n-1][2]);
}
};六、买卖股票的最佳时机(含手续费)
上一题用的是二维数组的第二维来表示多种状态,是因为状态比较多,如果像此题只有两种状态,就可以用两个函数,本质上是一样的。



class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
vector<int> f(n);
auto g = f;
f[0] = -prices[0];
for(int i = 1;i < n;i++){
f[i] = max(f[i-1],g[i-1] - prices[i]);
g[i] = max(g[i-1],f[i-1]+prices[i]- fee);
}
return g[n-1];
}
};七、买卖股票的最佳时机III


class Solution {
public:
const int INF = 0x3f3f3f3f;
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> f(n,vector<int>(3,-INF));
auto g = f;
f[0][0] = -prices[0];
g[0][0] = 0;
for(int i = 1;i < n;i++){
for(int j = 0;j < 3;j++){
f[i][j] = max(f[i-1][j],g[i-1][j] - prices[i]);
g[i][j] = g[i-1][j];
if(j >= 1)
g[i][j] = max(g[i-1][j],f[i-1][j-1]+prices[i]);
}
}
int ret = 0;
for(int i = 0;i < 3;i++){
ret = max(ret,g[n-1][i]);
}
return ret;
}
};八、买卖股票的最佳时机IV

class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
int n = prices.size();
k = min(k,n/2);
const int INF = 0x3f3f3f3f;
vector<vector<int>> f(n,vector<int>(k+1,-INF));//注意是k+1
auto g = f;
f[0][0] = -prices[0];
g[0][0] = 0;
for(int i = 1;i < n;i++){
for(int j = 0;j <= k;j++){
f[i][j] = max(f[i-1][j],g[i-1][j]-prices[i]);
g[i][j] = g[i-1][j];
if(j >= 1)
g[i][j] = max(g[i-1][j],f[i-1][j-1]+prices[i]);
}
}
int ret = 0;
for(int j = 0;j <= k;j++){
ret = max(ret,g[n-1][j]);
}
return ret;
}
};