本文是笔者在学习《信息论与编码》课程中所做的笔记，供个人学习记忆使用。
第三章 离散信源

一、离散信源

概念

若信源输出的消息为离散的符号形式，如手写文字，计算机输出的代码，则该信源称为离散信源。其输出的消息称为离散消息。可用下列符号序列表示：
……X-2X-1X0X1X2……。
其中，Xi是在第i时刻产生的符号，i为整数，Xi为一个随机变量。

离散无记忆信源

若离散信源输出的符号Xi相互独立，则称此信源为离散无记忆信源，否则称为离散有记忆信源。

若输出符号间彼此相关，且每个符号只与它前面的一个符号相关，而这种相关性可以用符号间的转移概率来描述，则称之为马尔可夫信源。

K重符号序列离散信源

若离散信源每次发出一个符号来作为一条消息，则称为单符号离散信源；若每次发出K个符号作为一条消息，则称为K重符号序列离散信源。

二、离散信源的熵

单符号离散无记忆信源熵

若信源X含有M个符号，而且每个符号相互独立，则当信源每次发送一个符号代表一条消息时，其信源熵可以表示为:

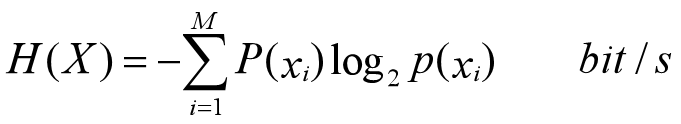
K重符号序列离散无记忆信源熵

若信源X含有M个符号，而且每个符号相互独立，则当信源每次发送K个符号代表一条消息时，其信源熵可以表示成为：

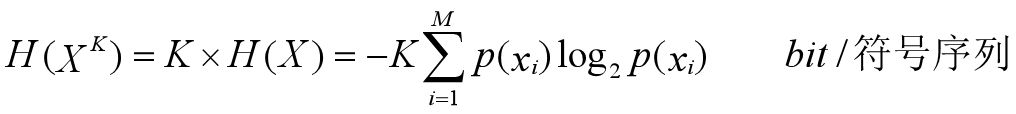
K重符号序列离散有记忆信源熵

若信源X含有M个符号，但是每个符号间是不独立的，则当该信源每次发出K个符号代表一条消息时，其信源熵满足: H(XK)<KH(X).

如果信源符号之间具有相关性，则每次发出K个符号代表一条消息时对外提供的平均信息量比符号间相互独立时每次发出K个符号代表一条消息所提供的平均信息量要小。

而且相关程度越大，其对外所能提供的平均信息量越小。

马尔可夫信源熵

马尔可夫信源从状态Si 发生转移发出一个信源符号的条件熵

设马尔可夫信源当前时刻处于L个状态中的第i个状态，下一个时刻转移到K个状态中的某一个，P(Sj|Si)是马尔可夫信源从状态Si 转到Sj的转移概率， 则马尔可夫信源从状态Si 发生转移发出一个信源符号的条件熵定义为：

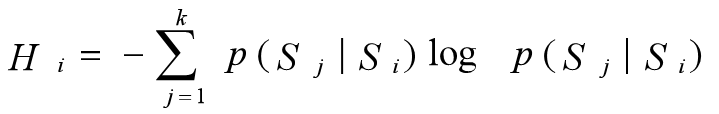
马尔可夫的信源熵

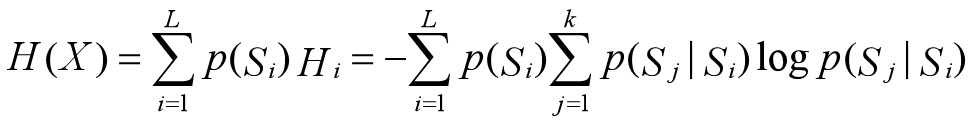
三、离散信源的时间熵

离散信源的时间熵是指信源在单位时间（秒）内对外所能够提供的信息量，而不管信源是单符号信源还是符号序列信源。或者说，时间熵反映了信源对外提供信息量的速度。

单符号离散无记忆信源的时间熵

设信源X含有M个符号，而且符号相互独立，第i个符号xi出现的概率是P(xi)，时间长度为bi，则该信源的时间熵定义为：Ht(X)=H(X)/b. 其中b为信源符号的平均时间长度。

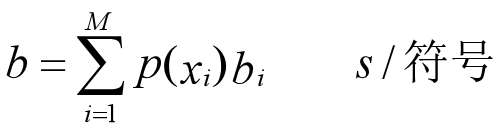
K重符号序列离散无记忆信源的时间熵

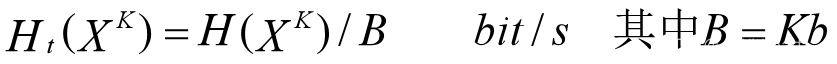
由于信源无记忆，上式也可以写成：

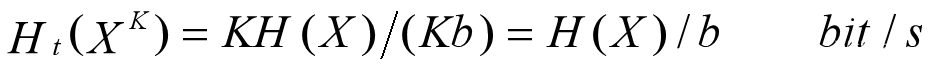
可以看到，K重符号序列离散无记忆信源对外提供信息量的速度与单符号无记忆信源相同。

K重符号序列离散有记忆信源的时间熵

由于信源有记忆，所以有：

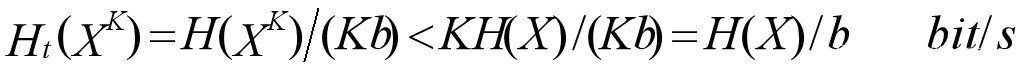
有记忆信源与无记忆信源相比，对外提供信息量的速度下降了。

马尔可夫信源的时间熵

信源从状态Si发生转移并发出一个符号时，符号的平均长度

若信源从状态Si转移到状态Sj，发出的符号是xij，它的时间长度设为bij，则信源从状态Si发生转移并发出一个符号时，符号的平均长度为：

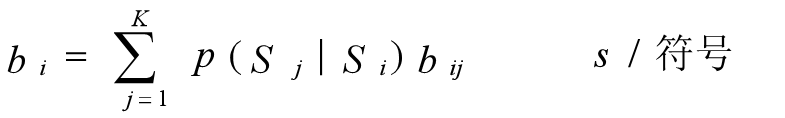
K为下一个时刻的状态数。信源从任意状态发生转移，并发出一个符号，符号的平均长度为：

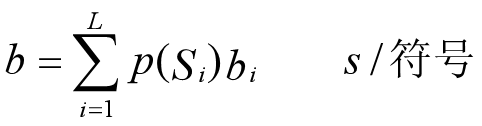
马尔可夫信源的时间熵

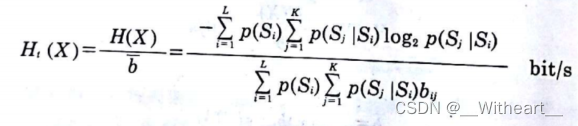
信源效率和冗余度

信源效率

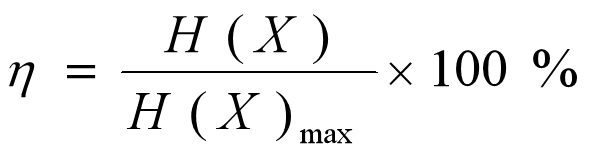
信源冗余度

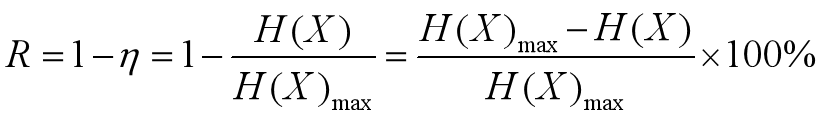
离散信源的无失真编码

其实很简单，
假设要表示的消息的总量是M条，
那么就要找到一个代码长度N使得D个符号可以表示M条消息
D^N>=M
没有不能表示的消息就叫无失真编码

信源编码速率

设离散信源输出的消息为K重符号序列消息，信源编码器采用D进制信道符号对离散消息进行编码，生成的D进制代码组的长度为N,则信源编码速率为：

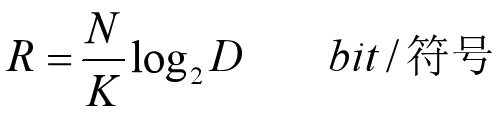
物理意义：代表一个K重符号序列消息被编成一个由N个码元组成的D进制代码组时，K重符号中的每一个字符所对应的由D进制码元的信息量。