github

python版本 

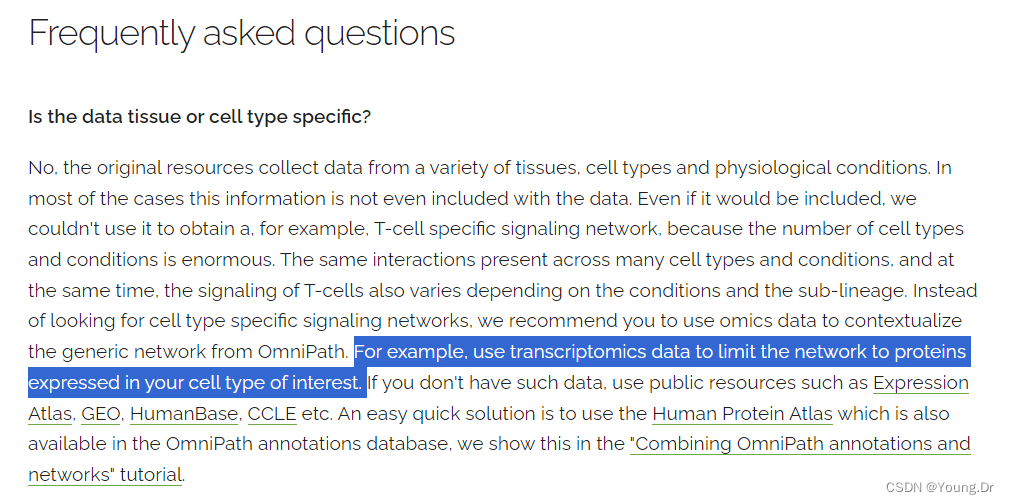
omnipath tutorials · Issue #17 · saezlab/omnipath (github.com)

R版本

saezlab/OmnipathR: R client for the OmniPath web service (github.com)https://github.com/saezlab/OmnipathR

GitHub - saezlab/OmnipathR: R client for the OmniPath web serviceR client for the OmniPath web service. Contribute to saezlab/OmnipathR development by creating an account on GitHub.https://github.com/saezlab/OmnipathR

OmnipathR: an R client for the OmniPath web service • OmnipathROmnipathRhttps://r.omnipathdb.org/articles/omnipath_intro.html

 

比较全 各种系列教程

OmniPath :: Workflows for using OmniPath (omnipathdb.org)https://workflows.omnipathdb.org/