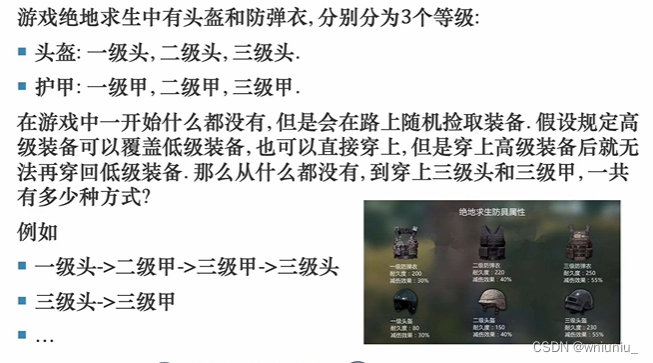
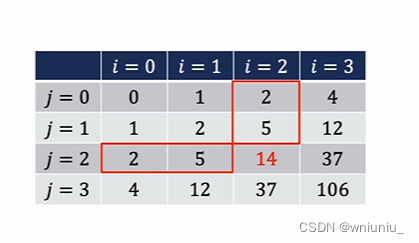
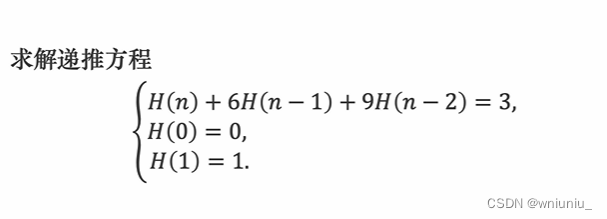离散数学 学习 之 递推方程和生成函数

news2024/10/7 16:17:10

递推方程

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

注意这里的特征根一定不是相等

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

特解的话一般要去设出基本的形式

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
这是0 次多项式

在这里插入图片描述
在这里插入图片描述

生成函数

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1084018.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Kepler.gl笔记：地图交互

Kepler.gl笔记：地图交互

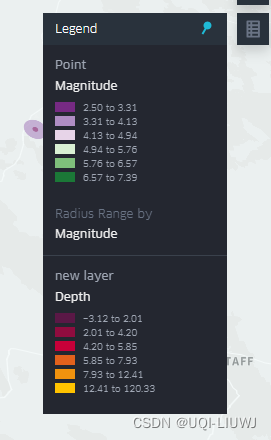
1 双图 点第一个图标，进入双图 双图可以选择各自显示哪些layer 2 2D图转3D图 点击第二个图标 鼠标拖拽是控制位置 ctrl鼠标拖拽是旋转 3 显示图例
阅读更多...
10_博客管理系统

10_博客管理系统

1 项目展示 Express框架可以开发各种不同类型的项目，博客管理系统（Blog Management System）就是一个比较典型的项目。许多热爱分享技术的程序员都在建立自己的博客，用来发表一些技术文章。 主要完成用户登录、用户管理、文章管理…
阅读更多...
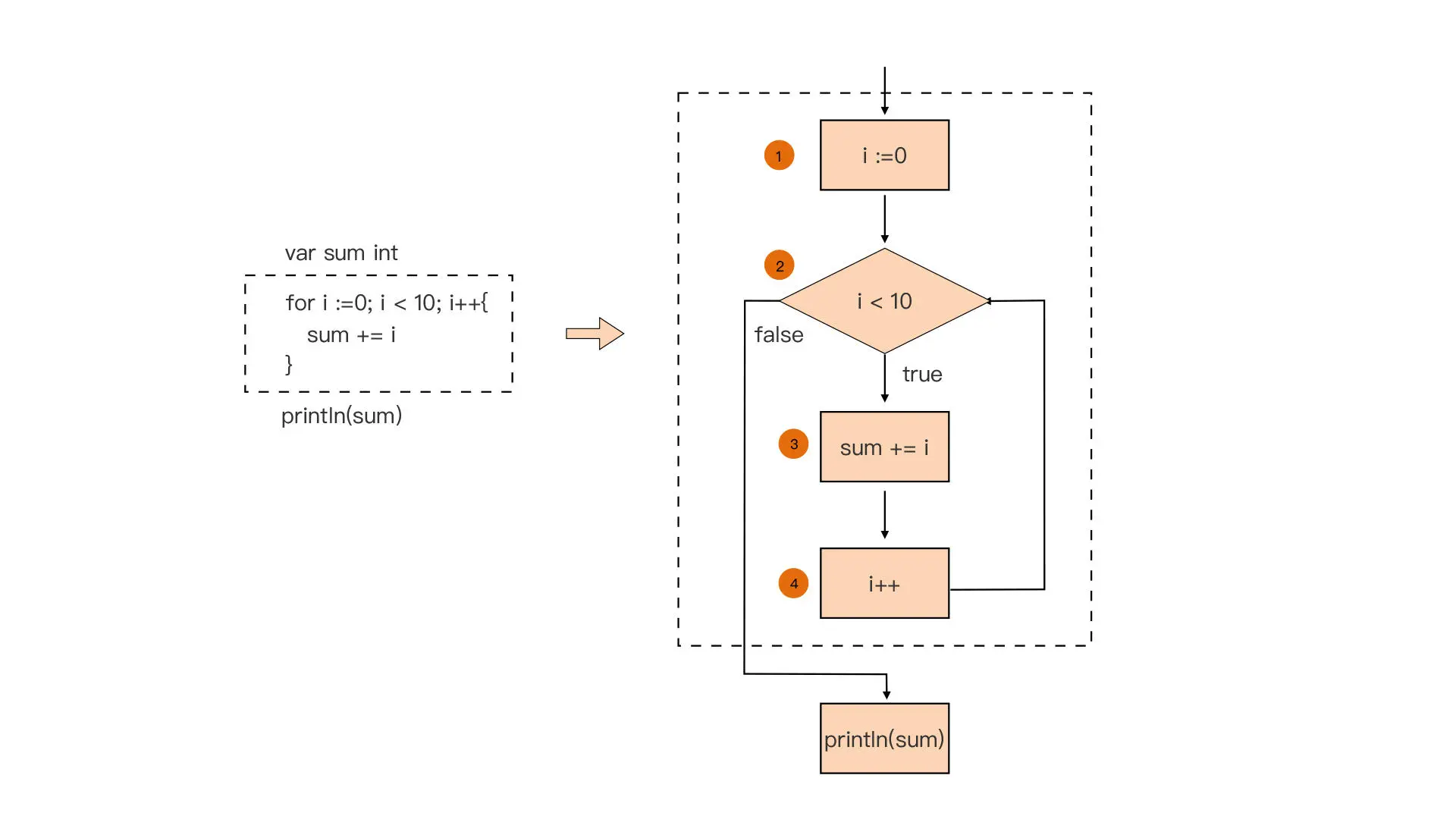
Go 循环之for循环，仅此一种

Go 循环之for循环，仅此一种

Go 循环之for循环，仅此一种 文章目录 Go 循环之for循环，仅此一种一、for 循环介绍二、for 循环结构2.1 基本语法结构2.2 省略初始值2.3 省略初始语句和结束语句2.4 无限循环2.5 for 循环支持声明多循环变量2.6 小练习：打印九九乘法表 三、for…
阅读更多...
随机颜色生成器

随机颜色生成器

项目需求&#xff1a; 要求随机生成颜色 HEX编码格式 快速了解色彩原理可查看&#xff1a;https://zhuanlan.zhihu.com/p/583033395 function randColor(){$str #;for($i 0; $i < 6; $i){ //对应HEX编码六位字符$randNum rand(0,15);switch ($randNum) {case 10: $ran…
阅读更多...
2、TCP协议基础

2、TCP协议基础

TCP协议基础 1、3次握手建立连接 SYN表示建立连接的标志位&#xff0c;ACK为应答标志位 #mermaid-svg-XQE5icHJvP0vkGP4 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-XQE5icHJvP0vkGP4 .error-icon{fill:#55222…
阅读更多...
js精度问题

js精度问题

1、问题场景&#xff1a;请求接口取得Number类型的数字和后端实际值不一致 比如&#xff1a; 后端返回10976458979374929&#xff0c;实际从接口拿到的是10976458979374928&#xff0c;在控制台也会得到这样的结果&#xff1a; 原因&#xff1a; 在JavaScript中&#xff0c;N…
阅读更多...
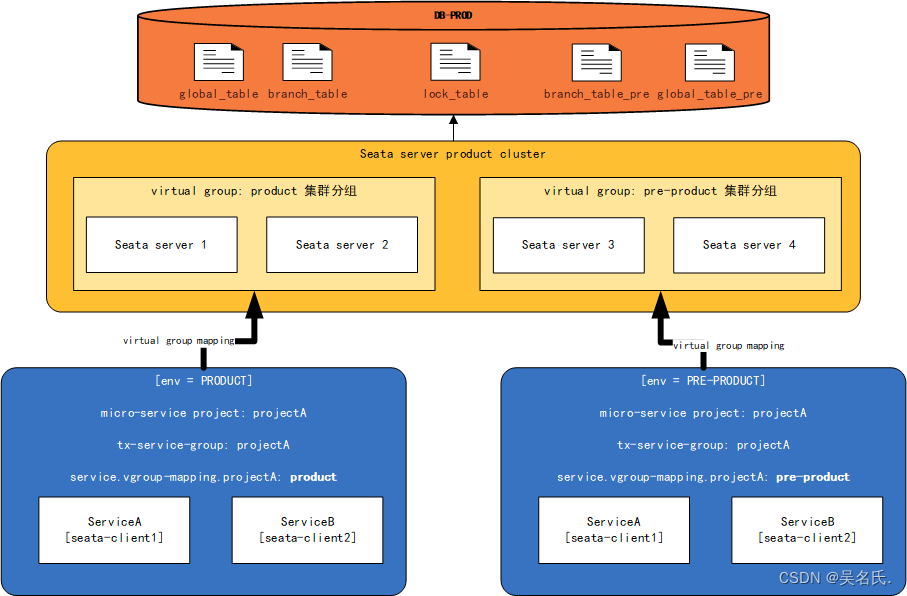
Seata入门系列【5】事务分组原理及应用案例详解

Seata入门系列【5】事务分组原理及应用案例详解

1 事务分组 1.1 概念 事务分组&#xff1a;seata的资源逻辑&#xff0c;可以按微服务的需要&#xff0c;在应用程序&#xff08;客户端&#xff09;对自行定义事务分组&#xff0c;每组取一个名字。 例如以下配置中&#xff0c;定义了当前事务分组名为${spring.application.…
阅读更多...
凉鞋的 Unity 笔记 108. 第二个通识：增删改查

凉鞋的 Unity 笔记 108. 第二个通识：增删改查

在这一篇&#xff0c;我们来学习此教程的第二个通识&#xff0c;即&#xff1a;增删改查。 增删改查我们不只是一次接触到了。 在最先接触的场景层次窗口中&#xff0c;我们是对 GameObject 进行增删改查。 在 Project 文件窗口中&#xff0c;我们是对文件&文件夹进行增删…
阅读更多...
Elasticsearch —索引性能技巧

Elasticsearch —索引性能技巧

目录 一、科学的测试性能 二、使用批量请求并调整其大小 三、存储 四、段和合并 五、其他 如果你是在一个索引负载很重的环境&#xff0c;比如索引的是基础设施日志&#xff0c;你可能愿意牺牲一些搜索性能换取更快的索引速率。在这些场景里&#xff0c;搜索常常是很少见的…
阅读更多...
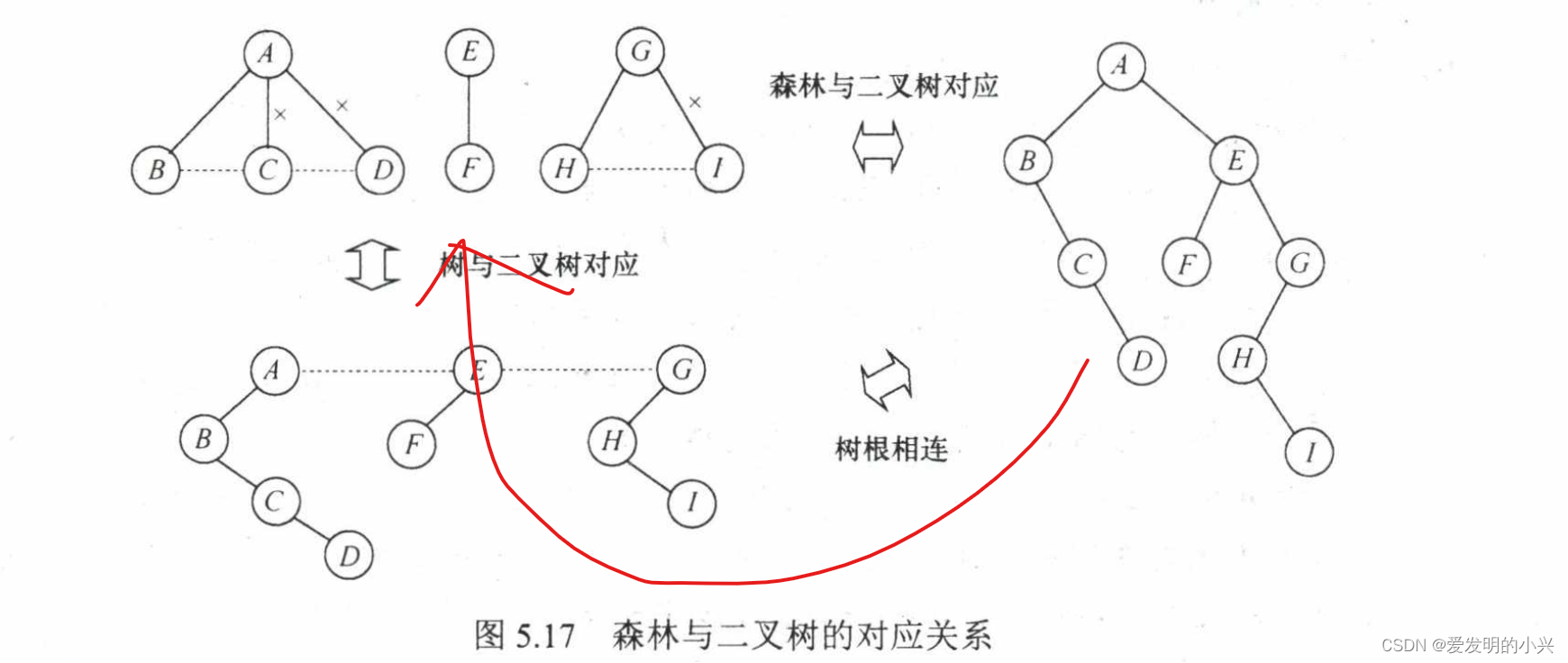
数据结构题型17-树、森林

数据结构题型17-树、森林

文章目录 1 树转换为二叉树2 森林转换为二叉树3 二叉树转换为树4 二叉树转换为森林 1 树转换为二叉树 参考博客&#xff1a;如何将一棵树转化成二叉树 2 森林转换为二叉树 参考博客&#xff1a;树、森林与二叉树的转换 3 二叉树转换为树 参考博客&#xff1a;树、森林与…
阅读更多...
开山之作 | YOLOv1算法超详细解析（包括诞生背景+论文解析+技术原理等）

开山之作 | YOLOv1算法超详细解析（包括诞生背景+论文解析+技术原理等）

前言&#xff1a;Hello大家好&#xff0c;我是小哥谈。目标检测是计算机视觉领域的一项重要研究方向&#xff0c;它在许多应用领域中都得到了广泛应用&#xff0c;如人脸识别、物体识别、自动驾驶、视频监控等。在过去&#xff0c;目标检测方法主要采用基于RCNN、Fast R-CNN等深…
阅读更多...
软件工程与计算总结（九）软件体系结构基础

软件工程与计算总结（九）软件体系结构基础

目录 ​编辑 一.体系结构的发展 二.理解体系结构 1.定义 2.区分体系结构的抽象与实现 3.部件 4.连接件 5.配置 三.体系结构风格初步 1.主程序/子程序 2.面向对象式 3.分层 4.MVC 一.体系结构的发展 小规模编程的重点在于模块内部的程序结构非常依赖于程序设计语言…
阅读更多...
学网络安全的过程 ，差点要了我的命

学网络安全的过程 ，差点要了我的命

我真的好像感慨一下&#xff0c;这个世界真的给计算机应届生留活路了吗&#xff1f; 看着周围的同学&#xff0c;打算搞前端、JAVA、C、C的&#xff0c;一个两个去跑去应聘。你以为是00后整治职场&#xff1f; 真相是主打一个卑微&#xff1a;现阶段以学习为主&#xff08;工资…
阅读更多...
在Linux中掌握不同的命令，让创建文件变得易如反掌

在Linux中掌握不同的命令，让创建文件变得易如反掌

在Linux中创建一个新文件很简单，但也有一些令人惊讶和灵巧的技术。​在本教程中，学习如何从Linux终端创建文件。​ 先决条件 访问命令行/终端窗口（Ctrl-Alt-F2或Ctrl-Alt-T） 具有sudo权限的用户帐户（对于某些文件/目录是可选的） 从命令行创建新的Linux文件 Linux的设计…
阅读更多...
TXT文件恢复，简单3招，快速恢复文件！

TXT文件恢复，简单3招，快速恢复文件！

“由于工作需要&#xff0c;我的电脑中保存了很多的TXT文件&#xff0c;但是在清内存时&#xff0c;我不小心删除了一些比较重要的文件&#xff0c;请问有什么方法可以恢复吗&#xff1f;” TXT文件是一种普通的文本文件格式&#xff0c;它包含了纯文本信息&#xff0c;没有任何…
阅读更多...
股票价格预测 | Python基于RNN及股票预测实战

股票价格预测 | Python基于RNN及股票预测实战

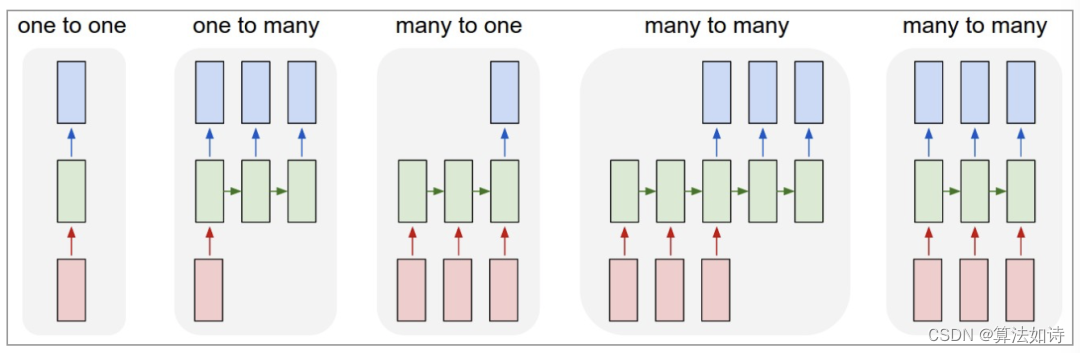
循环神经网络（RNN）是基于序列数据（如语言、语音、时间序列）的递归性质而设计的，是一种反馈类型的神经网络，其结构包含环和自重复，因此被称为“循环”。它专门用于处理序列数据，如逐字生成文本或预测时间序列数据(例如股票价格)。 （1）one to one：其实和全连接神经网络…
阅读更多...
Pycharm 2023 设置远程调试

Pycharm 2023 设置远程调试

pycharm 版本 &#xff1a; 2023.2.1 整体流程参考&#xff1a;https://blog.csdn.net/xuanhaolaile/article/details/128293254 首先确定远程服务器上已经安装好 requirements.txt 中所需的依赖包。 1、SSH Configurations 添加远程服务器 2、Python Interpreter 注意&…
阅读更多...
别再使用循环的方式筛选元素了！开发常用的Stream流+Lambda表达式过滤元素了解过吗？10000字超详细解析

别再使用循环的方式筛选元素了！开发常用的Stream流+Lambda表达式过滤元素了解过吗？10000字超详细解析

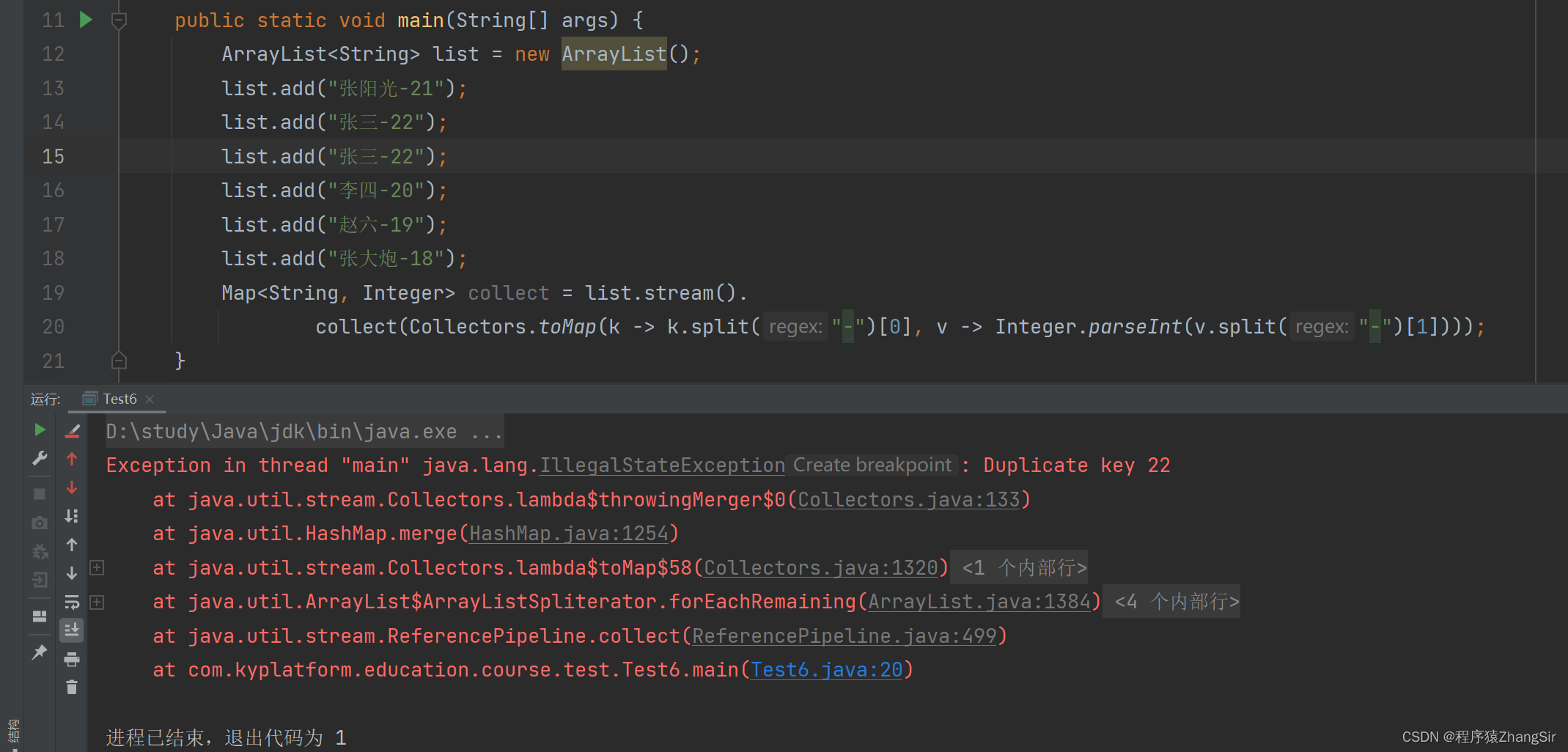
目录 1. Stream 流的简单展示 1.1 抛出问题 1.2 传统解决问题的编码方式 1.3 Stream 流的方式过滤元素 2. Stream 流的核心思想 3. Stream 流的使用 3.1 获取 stream 流 3.1.1 单列集合获取 stream 流 3.1.2 双列集合获取 stream 流 3.1.3 数组获取 stream 流 3.1.4…
阅读更多...
AD20统一修改相同元器件的名称和标号的方法

AD20统一修改相同元器件的名称和标号的方法

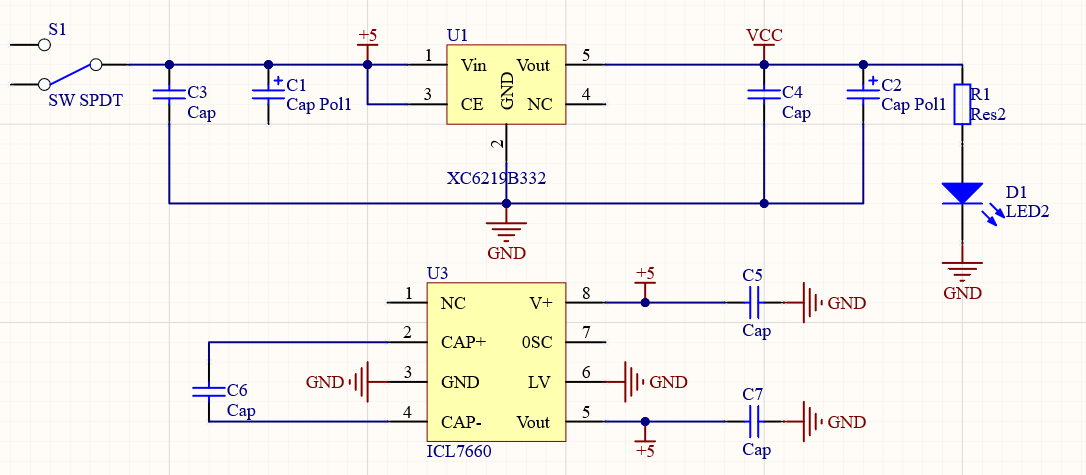
如图所示&#xff0c;我们原理图中有很多开关&#xff0c;比如说名字乱七八遭&#xff0c;想要整体快速修改应该怎么办呢&#xff1f; 解决方法&#xff1a;把鼠标指针放到原理图的空白处单击鼠标右键 点击查找相似对象之后鼠标变成了一个十字状&#xff0c;用十字状中心点击要…
阅读更多...
凉鞋的 Godot 笔记 108. 第二个通识：增删改查

凉鞋的 Godot 笔记 108. 第二个通识：增删改查

在这一篇&#xff0c;我们来学习此教程的第二个通识&#xff0c;即&#xff1a;增删改查。 增删改查我们不只是一次接触到了。 在最先接触的场景窗口中&#xff0c;我们是对 Node 进行增删改查。 在文件系统窗口中&#xff0c;我们是对文件&文件夹进行增删改查&#xff1…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023