-
可以把PyTorch简单看成是Python的深度学习第三方库,在PyTorch中定义了适用于深度学习的基本数据结构——
张量,以及张量的各类计算。其实也就相当于NumPy中定义的Array和对应的科学计算方法,正是这些基本数据类型和对应的方法函数,为我们进一步在PyTorch上进行深度学习建模提供了基本对象和基本工具。因此,在正式使用PyTorch进行深度学习建模之前,我们需要熟练掌握PyTorch中张量的基本操作方法。张量作为数组的衍生概念,其本身的定义和使用方法和NumPy中的Array非常类似,甚至,在复现一些简单的神经网络算法场景中,我们可以直接使用NumPy中的Array来进行操作。 -
张量的最基本创建方法和NumPy中创建Array的格式一致,都是
创建函数(序列)的格式:张量创建函数:torch.tensor()-
t = torch.tensor([[0,1], [2,3]]) # 通过列表创建张量 # 通过元组创建张量 # torch.tensor((1, 2)) # 通过数组创建张量 # a = np.array((1, 2)) # t = torch.tensor(a) # 整数型的数组默认创建int32(整型)类型,而张量则默认创建int64(长整型)类型。 # 创建浮点型数组时,张量默认是float32(单精度浮点型),而Array则是默认float64(双精度浮点型)。 print(t,t.data) print(id(t),id(t.data)) ## 输出 ## tensor([[0, 1], [2, 3]]) tensor([[0, 1], [2, 3]]) 2036011697072 2036018540848 -
两者返回不同的id,但是共享同一个内存
-
t[0][0]=10 t.data[1][0]=20 print(t,t.data) print(id(t),id(t.data)) ## 输出 ## tensor([[10, 1], [20, 3]]) tensor([[10, 1], [20, 3]]) 2036011697072 2036019332576 -
属性 grad(导数), grad-fn(张量所在的导数函数), requires_grad(是否执行可导的判定)。调用backward计算导数,导数是累加的,如果每次单独计算,需要清空梯度
optimiter.zero_grad()。 -
属性 is_leaf, retain_grad。判定该元素在计算图中是否为叶子节点,当为叶子节点时,它的属性requires_grad为False。当requires_grad为True,但是用户构建的Tensor,表示该张量不是计算结果,而是用户构建的初始化张量。在用backward后,仅只有 leaf tensor 才会有 grad 属性。如果不是 leaf tensor 需要retain_grad 函数开启grad。
-
属性ndim和dim函数,查看tensor的维度;属性shape和size(),tensor的形状
-
t=torch.cat([t,t],0) print(t.ndim,len(t),t.dim()) print(t.shape,t.size()) ## 输出 ## 2 8 2 torch.Size([8, 2]) torch.Size([8, 2]) -
和数组不同,对于张量而言,数值型和布尔型张量就是最常用的两种张量类型,相关类型总结如下。
-
数据类型 dtype 32bit浮点数 torch.float32或torch.float 64bit浮点数 torch.float64或torch.double 16bit浮点数 torch.float16或torch.half 8bit无符号整数 torch.unit8 8bit有符号整数 torch.int8 16bit有符号整数 torch.int16或torch.short 32bit有符号整数 torch.int32或torch.int 64bit有符号整数 torch.int64或torch.long 布尔型 torch.bool 复数型 torch.complex64
-
-
创建int16整型张量; torch.tensor([1.1, 2.7], dtype = torch.int16)
-
在PyTorch中也支持复数类型对象创建; a = torch.tensor(1 + 2j) # 1是实部、2是虚部; tensor(1.+2.j)
-
和NumPy中array相同,当张量各元素属于不同类型时,系统会自动进行隐式转化。在使用方法进行类型转化时,方法名称则是double。(虽然torch.float和double都表示双精度浮点型。)
-
-
flatten拉平:将任意维度张量转化为一维张量,按行排列,拉平。注:如果将零维张量使用flatten,则会将其转化为一维张量。
-
reshape方法:任意变形;注意,reshape过程中维度的变化:reshape转化后的维度由该方法输入的参数“个数”决定。
-
在很多数值科学计算的过程中,都会创建一些特殊取值的张量,用于模拟特殊取值的矩阵,如全0矩阵、对角矩阵等。因此,PyTorch中也存在很多创建特殊张量的函数。
-
torch.zeros([2, 3]) # 创建全是0的,两行、三列的张量(矩阵) torch.ones([2, 3]) # 注:由于zeros就已经确定了张量元素取值,因此该函数传入的参数实际上是决定了张量的形状 -
单位矩阵
-
torch.eye(5) ## tensor([[1., 0., 0., 0., 0.], [0., 1., 0., 0., 0.], [0., 0., 1., 0., 0.], [0., 0., 0., 1., 0.], [0., 0., 0., 0., 1.]]) -
在PyTorch中,需要利用一维张量去创建对角矩阵。
-
t1 = torch.tensor([1, 2]) torch.diag(t1) # 不能使用list直接创建对角矩阵,diag(): argument 'input' (position 1) must be Tensor, not list ## tensor([[1, 0], [0, 2]]) -
rand:服从0-1均匀分布的张量
-
torch.randn(2, 3) torch.normal(2, 3, size = (2, 2)) # 均值为2,标准差为3的张量;normal:服从指定正态分布的张量 torch.randint(1, 10, [2, 4]) # 在1-10之间随机抽取整数,组成两行四列的矩阵,randint:整数随机采样结果 -
arange/linspace:生成数列
-
torch.arange(5) # 和range相同;tensor([0, 1, 2, 3, 4]) torch.arange(1, 5, 0.5) # 从1到5(左闭右开),每隔0.5取值一个 torch.linspace(1, 5, 3) # 从1到5(左右都包含),等距取三个数;tensor([1., 3., 5.]) -
empty:生成未初始化的指定形状矩阵
-
torch.empty(2, 3) ## tensor([[6.8664e-44, 6.8664e-44, 1.1771e-43], [6.7262e-44, 7.0065e-44, 8.1275e-44]]) torch.full([2, 4], 2) tensor([[2, 2, 2, 2], [2, 2, 2, 2]]) -
还能根据指定对象的形状进行数值填充,只需要在上述函数后面加上
_like即可。 -
torch.full_like(t1, 2) # 根据t1形状,填充数值2 torch.randint_like(t2, 1, 10) # 根据t1形状,填充数值1-10,不包括10的整数 t1 = torch.tensor([1, 2]) torch.randn_like(t1) # t1是整数,而转化后将变为浮点数,此时代码将报错,"normal_kernel_cpu" not implemented for 'Long' -
张量、数组和列表是较为相似的三种类型对象,在实际操作过程中,经常会涉及三种对象的相互转化。在此前张量的创建过程中,我们看到torch.tensor函数可以直接将数组或者列表转化为张量,而我们也可以将张量转化为数组或者列表。
-
t1 = torch.tensor([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) t1.numpy() # array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=int64) import numpy as np # 当然,也可以通过np.array函数直接转化为array np.array(t1) # array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=int64) t1# tensor([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) # .tolist方法:张量转化为列表 t1.tolist() # [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] -
list函数:张量转化为列表
-
[tensor(1), tensor(2), tensor(3), tensor(4), tensor(5), tensor(6), tensor(7), tensor(8), tensor(9), tensor(10)] # 需要注意的是,此时转化的列表是由一个个零维张量构成的列表,而非张量的数值组成的列表。 -
在很多情况下,我们需要将最终计算的结果张量转化为单独的数值进行输出,此时需要使用.item()方法来执行。
-
Python中其他对象类型一样,等号赋值操作实际上是浅拷贝,需要进行深拷贝,则需要使用clone方法
-
-
张量作为有序的序列,也是具备数值索引的功能,并且基本索引方法和Python原生的列表、NumPy中的数组基本一致,当然,所有不同的是,PyTorch中还定义了一种采用函数来进行索引的方式。张量也是有序序列,我们可以根据每个元素在系统内的顺序“编号”,来找出特定的元素,也就是索引。张量索引出来的结果还是零维张量, 而不是单独的数。要转化成单独的数,需要使用item()方法。
在张量的索引中,step位必须大于0 -
二维张量的索引逻辑和一维张量的索引逻辑基本相同,二维张量可以视为两个一维张量组合而成,而在实际的索引过程中,需要用逗号进行分隔,分别表示对哪个一维张量进行索引、以及具体的一维张量的索引。对二维张量来说,基本可以视为是对矩阵的索引,并且行、列的索引遵照相同的索引规范,并用逗号进行分隔。
-
import torch t2 = torch.arange(1, 10).reshape(3, 3) t2 t2[0, 1] # 表示索引第一行、第二个(第二列的)元素 tensor(2) t2[0][1]# 表示索引第一行、第二个(第二列的)元素 tensor(2) t2[0, ::2]# 表示索引第一行、每隔两个元素取一个 tensor([1, 3]) t2[0, [0, 2]] # 索引结果同上 t2[::2, ::2] # 表示每隔两行取一行、并且每一行中每隔两个元素取一个 tensor([[1, 3], [7, 9]])
-
-
在二维张量索引的基础上,三维张量拥有三个索引的维度。我们将三维张量视作矩阵组成的序列,则在实际索引过程中拥有三个维度,分别是索引矩阵、索引矩阵的行、索引矩阵的列。
-
t3 = torch.arange(1, 28).reshape(3, 3, 3) t3 ## tensor([[[ 1, 2, 3], [ 4, 5, 6], [ 7, 8, 9]], [[10, 11, 12], [13, 14, 15], [16, 17, 18]], [[19, 20, 21], [22, 23, 24], [25, 26, 27]]]) t3[1, ::2, ::2] # 索引第二个矩阵,行和列都是每隔两个取一个 tensor([[10, 12], [16, 18]]) t3[:: 2, :: 2, :: 2] # 每隔两个取一个矩阵,对于每个矩阵来说,行和列都是每隔两个取一个 tensor([[[ 1, 3], [ 7, 9]], [[19, 21], [25, 27]]])
-
-
在PyTorch中,我们还可以使用index_select函数,通过指定index来对张量进行索引。在index_select函数中,第二个参数实际上代表的是索引的维度。对于t1这个一维向量来说,由于只有一个维度,因此第二个参数取值为0,就代表在第一个维度上进行索引。
-
t1 = torch.arange(10) indices = torch.tensor([1, 2]) # 需要tensor torch.index_select(t1, 0, indices) ## tensor([1, 2]) t2 = torch.arange(12).reshape(4, 3) ## tensor([[ 0, 1, 2], [ 3, 4, 5], [ 6, 7, 8], [ 9, 10, 11]]) torch.index_select(t2, 0, indices) ## tensor([[3, 4, 5], [6, 7, 8]])
-
-
在正式介绍张量的切分方法之前,需要首先介绍PyTorch中的.view()方法。该方法会返回一个类似视图的结果,该结果和原张量对象共享一块数据存储空间,并且通过.view()方法,还可以改变对象结构,生成一个不同结构,但共享一个存储空间的张量。当然,共享一个存储空间,也就代表二者是“浅拷贝”的关系,修改其中一个,另一个也会同步进行更改。“视图”的作用就是节省空间,而值得注意的是,在接下来介绍的很多切分张量的方法中,返回结果都是“视图”,而不是新生成一个对象。
-
chunk函数能够按照某维度,对张量进行均匀切分,并且返回结果是原张量的视图。
-
t2 = torch.arange(12).reshape(4, 3) tc = torch.chunk(t2, 4, dim=0) # 在第零个维度上(按行),进行四等分 ## 返回类型是元组 (tensor([[0, 1, 2]]), tensor([[3, 4, 5]]), tensor([[6, 7, 8]]), tensor([[ 9, 10, 11]]))# chunk返回结果是一个视图,不是新生成了一个对象 # 修改tc中的值,原张量也会对应发生变化 -
当原张量不能均分时,chunk不会报错,但会返回其他均分的结果
-
torch.chunk(t2, 3, dim=0) # 次一级均分结果 ## (tensor([[0, 1, 2], [3, 4, 5]]), tensor([[ 6, 7, 8], [ 9, 10, 11]]))
-
-
split既能进行均分,也能进行自定义切分。当然,需要注意的是,和chunk函数一样,split返回结果也是view。
-
t2 = torch.arange(12).reshape(4, 3) torch.split(t2, 2, 0) # 第二个参数只输入一个数值时表示均分,第三个参数表示切分的维度 torch.split(t2, [1, 3], 0)# 第二个参数输入一个序列时,表示按照序列数值进行切分,也就是1/3分 ## (tensor([[0, 1, 2]]), tensor([[ 3, 4, 5], [ 6, 7, 8], [ 9, 10, 11]])) torch.split(t2, [1, 1, 2], 0) ## (tensor([[0, 1, 2]]), tensor([[3, 4, 5]]), tensor([[ 6, 7, 8], [ 9, 10, 11]])) -
注意,当第二个参数位输入一个序列时,序列的各数值的和必须等于对应维度下形状分量的取值。例如,上述代码中,是按照第一个维度进行切分,而t2总共有4行,因此序列的求和必须等于4,也就是1+3=4,而序列中每个分量的取值,则代表切块大小。tensor的split方法和array的split方法有很大的区别,array的split方法是根据索引进行切分。
-
import numpy as np x = np.array([0,1,2,3,4,5,6,7,8]) print (np.split(x,[3,5,6,9])) ## [array([0, 1, 2]), array([3, 4]), array([5]), array([6, 7, 8]), array([], dtype=int32)]
-
-
张量的合并操作类似与列表的追加元素,可以拼接、也可以堆叠。PyTorch中,可以使用cat函数实现张量的拼接。
-
a = torch.zeros(2, 3) b = torch.ones(2, 3) c = torch.full((3, 3),2) torch.cat([a, b]) # 按照行进行拼接,dim默认取值为0 ## tensor([[0., 0., 0.], [0., 0., 0.], [1., 1., 1.], [1., 1., 1.]]) torch.cat([a, b], 1) # 按照列进行拼接 tensor([[0., 0., 0., 1., 1., 1.], [0., 0., 0., 1., 1., 1.]]) torch.cat([a, c], 1) # 形状不匹配时将报错 # Sizes of tensors must match except in dimension 1. Expected size 2 but got size 3 for tensor number 1 in the list. -
拼接的本质是实现元素的堆积,也就是构成a、b两个二维张量的各一维张量的堆积,最终还是构成二维向量。
-
-
堆叠函数:stack;和拼接不同,堆叠不是将元素拆分重装,而是简单的将各参与堆叠的对象分装到一个更高维度的张量里。
-
torch.stack([a, b]) # 堆叠之后,生成一个三维张量 tensor([[[0., 0., 0.], [0., 0., 0.]], [[1., 1., 1.], [1., 1., 1.]]]) torch.stack([a, b]).shape # torch.Size([2, 2, 3]) torch.stack([a, c]) # 维度不匹配时也会报错 # stack expects each tensor to be equal size, but got [2, 3] at entry 0 and [3, 3] at entry 1
-
-
通过reshape方法,能够灵活调整张量的形状。而在实际操作张量进行计算时,往往需要另外进行降维和升维的操作,当我们需要除去不必要的维度时,可以使用squeeze函数,而需要手动升维时,则可采用unsqueeze函数。
-
t = torch.zeros(1, 1, 3, 1) #t张量解释:一个包含一个三维的四维张量,三维张量只包含一个三行一列的二维张量。 ## tensor([[[[0.], [0.], [0.]]]]) torch.squeeze(t) # tensor([0., 0., 0.]) torch.squeeze(t).shape # torch.Size([3]) t1 = torch.zeros(1, 1, 3, 2, 1, 2) ## tensor([[[0., 0.], [0., 0.]], [[0., 0.], [0., 0.]], [[0., 0.], [0., 0.]]]) torch.squeeze(t1).shape # torch.Size([3, 2, 2]) -
简单理解,squeeze就相当于提出了shape返回结果中的1。unsqeeze函数:手动升维
-
torch.unsqueeze(t, dim = 0) # 在第1个维度索引上升高1个维度 torch.unsqueeze(t, dim = 2).shape # 在第3个维度索引上升高1个维度 torch.unsqueeze(t, dim = 4).shape # 在第5个维度索引上升高1个维度 -
注意理解维度和shape返回结果一一对应的关系,shape返回的序列有几个元素,张量就有多少维度。
-
-
作为PyTorch中执行深度学习的基本数据类型,张量(Tensor)也拥有非常多的数学运算函数和方法,以及对应的一系列计算规则。在PyTorch中,能够作用与Tensor的运算,被统一称作为算子。并且相比于NumPy,PyTorch给出了更加规范的算子(运算)的分类,从而方便用户在不同场景下调用不同类型的算子(运算)。PyToch总共为Tensor设计了六大类数学运算,分别是:
-
逐点运算(Pointwise Ops):指的是针对Tensor中每个元素执行的相同运算操作;
-
规约运算(Reduction Ops):指的是对于某一张量进行操作得出某种总结值;
-
比较运算(Comparison Ops):指的是对多个张量进行比较运算的相关方法;
-
谱运算(Spectral Ops):指的是涉及信号处理傅里叶变化的操作;
-
BLAS和LAPACK运算:指的是基础线性代数程序集(Basic Linear Algeria Subprograms)和线性代数包(Linear Algeria Package)中定义的、主要用于线性代数科学计算的函数和方法;
-
其他运算(Other Ops):其他未被归类的数学运算。
-
t1 = torch.arange(3) t = t1+t1 # tensor([0, 2, 4]) a=[2,3,4]+[1,2,3] # [2, 3, 4, 1, 2, 3] import numpy as np b=np.arange(3)+np.arange(3) # array([0, 2, 4]) -
广播的特性是在不同形状的张量进行计算时,一个或多个张量通过隐式转化,转化成相同形状的两个张量,从而完成计算的特性。但并非任何两个不同形状的张量都可以通过广播特性进行计算,因此,我们需要了解广播的基本规则及其核心依据。标量可以和任意形状的张量进行计算,计算过程就是标量和张量的每一个元素进行计算。
-
t1 + 1 # 1是标量,可以看成是零维 tensor([1, 2, 3]) t1 + torch.tensor(1) #tensor([1, 2, 3]) -
相同维度、不同形状的张量之间计算;两个张量的形状上有两个分量不同时,只要不同的分量仍然有一个取值为1,则仍然可以广播。
-

-
在理解相同维度、不同形状的张量广播之后,对于不同维度的张量之间的广播其实就会容易很多,因为对于不同维度的张量,我们首先可以将低维的张量升维,然后依据相同维度不同形状的张量广播规则进行广播。而低维向量的升维也非常简单,只需将更高维度方向的形状填充为1即可。
-
-
逐点运算主要包括数学基本运算、数值调整运算和数据科学运算三块,相关函数如下:
-
函数 描述 torch.add(t1,t2 ) t1、t2两个张量逐个元素相加,等效于t1+t2 torch.subtract(t1,t2) t1、t2两个张量逐个元素相减,等效于t1-t2 torch.multiply(t1,t2) t1、t2两个张量逐个元素相乘,等效于t1*t2 torch.divide(t1,t2) t1、t2两个张量逐个元素相除,等效于t1/t2 -
函数 描述 torch.abs(t) 返回绝对值 torch.ceil(t) 向上取整 torch.floor(t) 向下取整 torch.round(t) 四舍五入取整 torch.neg(t) 返回相反的数 -
虽然此类型函数是数值调整函数,但并不会对原对象进行调整,而是输出新的结果。而若要对原对象本身进行修改,则可考虑使用
方法_()的表达形式,对对象本身进行修改。此时方法就是上述同名函数。 -
数学运算函数 数学公式 描述 幂运算 torch.exp(t) $ y_{i} = e^{x_{i}} $ 返回以e为底、t中元素为幂的张量 torch.expm1(t) $ y_{i} = e^{x_{i}} $ - 1 对张量中的所有元素计算exp(x) - 1 torch.exp2(t) $ y_{i} = 2^{x_{i}} $ 逐个元素计算2的t次方。 torch.pow(t,n) $\text{out}_i = x_i ^ \text{exponent} $ 返回t的n次幂 torch.sqrt(t) $ \text{out}{i} = \sqrt{\text{input}{i}} $ 返回t的平方根 torch.square(t) $ \text{out}_i = x_i ^ \text{2} $ 返回输入的元素平方。 对数运算 torch.log10(t) $ y_{i} = \log_{10} (x_{i}) $ 返回以10为底的t的对数 torch.log(t) $ y_{i} = \log_{e} (x_{i}) $ 返回以e为底的t的对数 torch.log2(t) $ y_{i} = \log_{2} (x_{i}) $ 返回以2为底的t的对数 torch.log1p(t) $ y_i = \log_{e} (x_i $ + 1) 返回一个加自然对数的输入数组。 三角函数运算 torch.sin(t) 三角正弦。 torch.cos(t) 元素余弦。 torch.tan(t) 逐元素计算切线。 -
在数值科学计算中,expm1函数和log1p函数是一对对应的函数关系,后面再介绍log1p的时候会讲解这对函数的实际作用。开根号也就相当于0.5次幂
-
log1p是进行$ y_i = \log_{e} (x_i $ + 1)计算,而expm则是进行$ y_{i} = e^{x_{i}} $ - 1计算,二者互为逆运算。
-
-
需要注意的是,虽然Python是动态编译的编程语言,但在PyTorch中,由于会涉及GPU计算,因此很多时候元素类型不会在实际执行函数计算时进行调整。此处的科学运算大多数都要求对象类型是浮点型,我们需要提前进行类型转化。
-
而log1p的实际应用场景有两个,其一是进行数据分布转化操作,另一种则是防止极小的数在进行对数运算时丢失有效位数。
-
大多数的数理统计分析,在建模过程中,都对数据的分布有较为严格的要求,但真实的数据往往不能满足特定的分布,因此很多时候我们会先对其进行一定程度上的数值转化,而log运算就是常用的将偏态分布的数据转化为高斯分布所使用的函数,并且在此过程中,log1p的效果往往会好于log的效果;
-
另一种使用场景,当处理的数据数值非常小时,使用对数运算往往会因为精度不够而使得计算无法进行(log0没有数学意义),此时使用log1p则可很好的避免这种情况。
-
m = torch.tensor(-2.6529) * 1e-20 # tensor(-2.6529e-20) # 转化为一个趋近于1的数再运算 torch.log1p(m) # tensor(-2.6529e-20) # 此时直接使用log无法执行运算 torch.log(m) # tensor(nan) # 无法运算就无法还原 torch.exp(torch.log(m)) # tensor(nan) # 无损还原 torch.expm1(torch.log1p(m)) # tensor(-2.6529e-20) -
在很多场景中,由于计算精度问题导致无法计算,并进一步导致数据信息损失,将会是非常致命的,典型场景如PCA主成分分析,相关问题会在算法讲解中进一步讨论。
-
-
在PyTorch中,sort排序函数将同时返回排序结果和对应的索引值的排列。
-
t = torch.tensor([1.0, 3.0, 2.0]) # 升序排列 torch.sort(t) ## torch.return_types.sort( values=tensor([1., 2., 3.]), indices=tensor([0, 2, 1])) # 降序排列 torch.sort(t, descending=True) ## torch.return_types.sort( values=tensor([3., 2., 1.]), indices=tensor([1, 2, 0]))
-
-
规约运算指的是针对某张量进行某种总结,最后得出一个具体总结值的函数。此类函数主要包含了数据科学领域内的诸多统计分析函数,如均值、极值、方差、中位数函数等等。
-
函数 描述 torch.mean(t) 返回张量均值 torch.var(t) 返回张量方差 torch.std(t) 返回张量标准差 torch.var_mean(t) 返回张量方差和均值 torch.std_mean(t) 返回张量标准差和均值 torch.max(t) 返回张量最大值 torch.argmax(t) 返回张量最大值索引 torch.min(t) 返回张量最小值 torch.argmin(t) 返回张量最小值索引 torch.median(t) 返回张量中位数 torch.sum(t) 返回张量求和结果 torch.logsumexp(t) 返回张量各元素求和结果,适用于数据量较小的情况 torch.prod(t) 返回张量累乘结果 torch.dist(t1, t2) 计算两个张量的闵式距离,可使用不同范式; torch.dist(t1, t2, 2) torch.topk(t) 返回t中最大的k个值对应的指标; torch.topk(t, 2)
-
-
dist函数可计算闵式距离(闵可夫斯基距离),通过输入不同的p值,可以计算多种类型的距离,如欧式距离、街道距离等。闵可夫斯基距离公式如下: $ D(x,y) = (\sum{n}_{u=1}|x_u-y_u|{p})^{1/p}$
-
由于规约运算是一个序列返回一个结果,因此若是针对高维张量,则可指定某维度进行计算。
-
# 创建一个3*3的二维向量 t2 = torch.arange(12).float().reshape(3, 4) # 按照第一个维度求和(每次计算三个)、按列求和 torch.sum(t2, dim = 0) # tensor([12., 15., 18., 21.]) # 按照第二个维度求和(每次计算四个)、按行求和 torch.sum(t2, dim = 1) # tensor([ 6., 22., 38.])
-
-
比较运算是一类较为简单的运算类型,和Python原生大的布尔运算类似,常用于不同张量之间的逻辑运算,最终返回逻辑运算结果(逻辑类型张量)。基本比较运算函数如下所示:
-
函数 描述 torch.eq(t1, t2) 比较t1、t2各元素是否相等,等效== torch.equal(t1, t2) 判断两个张量是否是相同的张量 torch.gt(t1, t2) 比较t1各元素是否大于t2各元素,等效> torch.lt(t1, t2) 比较t1各元素是否小于t2各元素,等效< torch.ge(t1, t2) 比较t1各元素是否大于或等于t2各元素,等效>= torch.le(t1, t2) 比较t1各元素是否小于等于t2各元素,等效<= torch.ne(t1, t2) 比较t1、t2各元素是否不相同,等效!=
-
pytorch的基本运算,是不是共享了内存,有没有维度变化
news2026/2/13 23:00:37
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1082032.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
并购交易:Truist Financial正在商谈以100亿美元将保险经纪业务出售
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,纽交所上市公司Truist Financial(TFC)正在商谈以100亿美元将保险经纪业务出售给Stone Point Capital。 这笔交易可能会加强Truist Financial的资本状况,在监管机构试图提高大型银行的资…
[CISCN 2019初赛]Love Math - RCE(异或绕过)
[CISCN 2019初赛]Love Math 1 解题流程1.1 分析1.2 解题题目代码:
<?php
//听说你很喜欢数学,不知道你是否爱它胜过爱flag
if(!isset($_GET[c]))
【Python】QTreeWidget树形结构添加
源码:
# 参考网址: https://blog.csdn.net/weixin_42286052/article/details/129532631
import os.path
import sys
from PySide6.QtWidgets import QApplication,QMainWindow,QHBoxLayout,QVBoxLayout,QPushButton,QTreeWidget,QTreeWidgetItem,QTreeW…
抖音自动养号脚本+抖音直播控场脚本
功能描述
一.抖音功能
1.垂直浏览
2.直播暖场
3.精准引流
4.粉丝留言
5.同城引流
6.取消关注
7.万能引流
8.精准截流
9.访客引流
10.直播间引流
11.视频分享
12.榜单引流
13.搜索引流
14.点赞回访
15.智能引流
16.关注回访 介绍下小红书数据挖掘
搜索关键词&…
uml简单用例图怎么画(要素,文字形式)
参与者(三类):人,外部系统,设备
用例: 系统外部可见的用例单元 表示前俩的关系:带箭头的实线(参与者1——用例1) 【实线为了观看我标红了,实际没有的】
1.i…
vue实现一个简单导航栏
Vue之简单导航栏
在vue中,想要实现导航栏的功能,除了用传统的a标签以外,还可以使用路由——vue-router来实现,前端小白在此记录一下学习过程(默认已经搭建好vue的脚手架环境):
建立项目并安装…
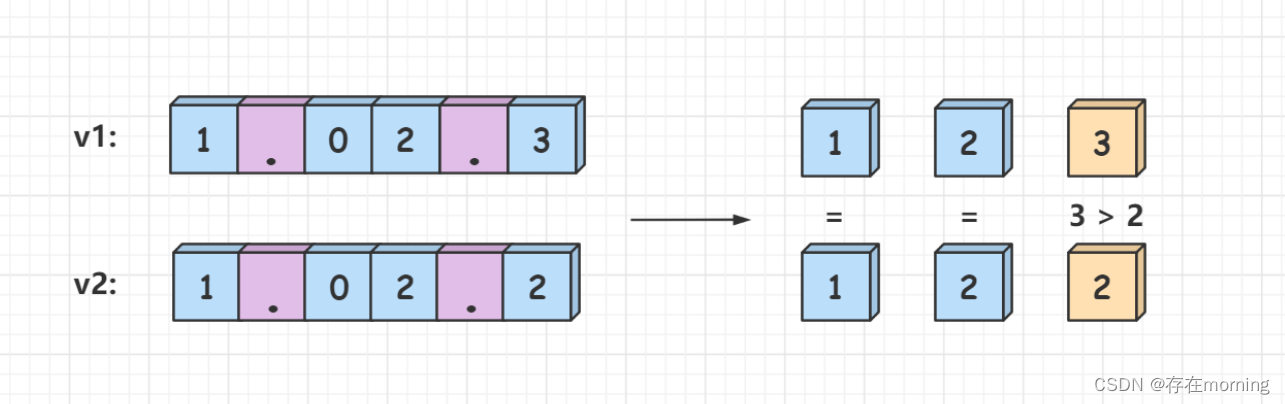
【数据结构-字符串 四】【字符串识别】字符串转为整数、比较版本号
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【字符串转换】,使用【字符串】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…
Andriod学习笔记(一)
写在前面的话 App开发的编程语言Java和KotlinXML App连接的数据库App工程目录结构模块级别的编译配置文件清单文件 界面显示与逻辑处理 安卓是一种基于Linux内核的自由及开放源代码的操作系统,主要使用于移动设备。 Mininum SDK表示安卓该版本以上的设备都可以运行该…
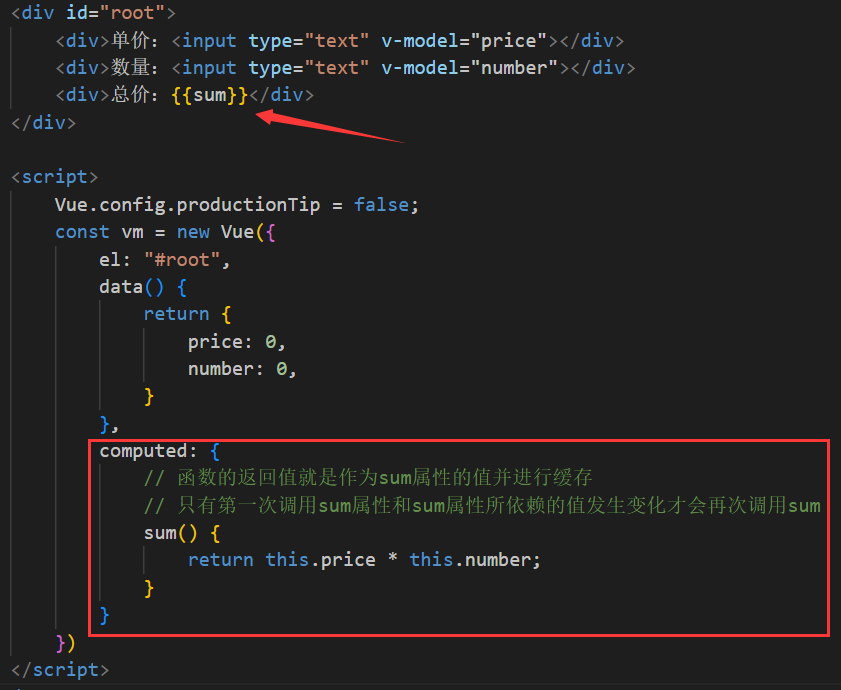
Vue计算属性的使用
当我们想要通过data中运算得到一个新的数据时,我们就可以使用计算属性。比如:data里的单价price和数量number可以相乘计算总价sum,这个sum我们就称为计算属性。
计算属性的语法格式: computed:{ 计算属性名称 ( ) { return 计算…
LAS Spark 在 TPC-DS 的优化揭秘
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 文章主要介绍了火山引擎湖仓一体分析服务 LAS Spark(下文以 LAS Spark 指代)在 TPC-DS 上的性能突破与优化策略。TPC-DS 是一个模拟复杂数据…
4、在 CentOS 8 系统上安装 pgAdmin 4
pgAdmin 4 是一个开源的数据库管理工具,专门用于管理和操作 PostgreSQL 数据库系统。它提供了一个图形用户界面(GUI),使用户能够轻松地连接到 PostgreSQL 数据库实例,执行 SQL 查询,管理数据库对象…
网络拓扑自动扫描工具
topology-scanner
Topology-Scanner是WeOps团队免费开放的一个网络拓扑自动扫描模块,可以自动发现网络设备的类型、网络设备之间的互联
使用方式
java -jar ./topology-scanner.jar --config_path./config/
配置说明
1. 拓扑发现请求参数文件(request.json)
i…
Web3 新手攻略:9 个不可或缺的 APP 助力你踏入加密领域
Web3世界充满了无限机遇,但要掌握它,您需要合适的工具���。今天,我将为您介绍9款Web3必备APP,涵盖钱包、DEX、和工具三大类别。而且,我要特别强烈推荐一个强大的钱包——Bitget Wall…
基于java+vue+springboot的家庭理财记账信息网站
运行环境
开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven
项目介绍
在这科技…
Bitxhub跨链平台
BitXHub跨链平台 跨链系统架构 过程
在跨链合约中调用统一写好的Broker合约Broker合约抛出事件由Plugin捕获到封装成平台统一的数据结构提交到中继链中目的链的跨链网关从中继链中同步IBTP数据结构网关将该数据结构通过Plugin提交到目的链
中继链体系架构 中继链的模块和流程…
【Vue面试题十七】、你知道vue中key的原理吗?说说你对它的理解
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:你知道vue中key的原理吗…
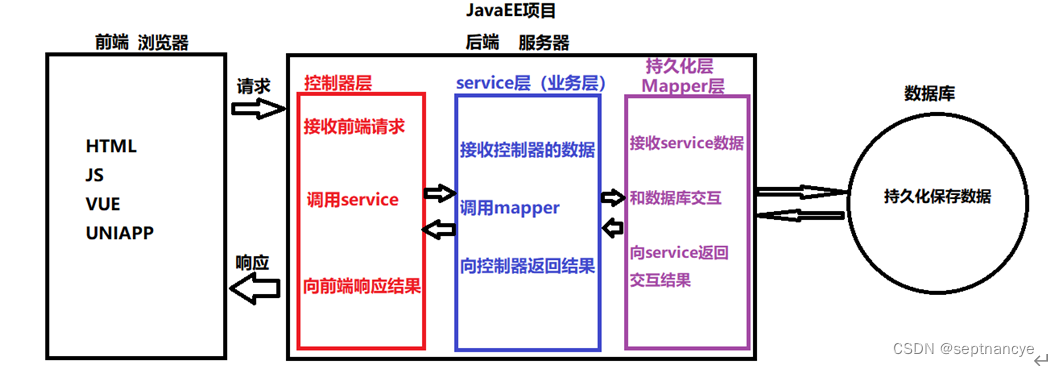
10.本项目的简单介绍及所用工具
本项目的简单介绍及所用工具 本项目的层次架构适合初学者或者有一些基础的同学,项目整体简单明了,有着非常严谨的逻辑思维,并且在前面文章中也讲了一些项目中所需要的软件安装配置以及一些前置的在本项目中所需要的java基础知识。 项目名称
…
几种预训练模型微调方法和peft包的使用介绍
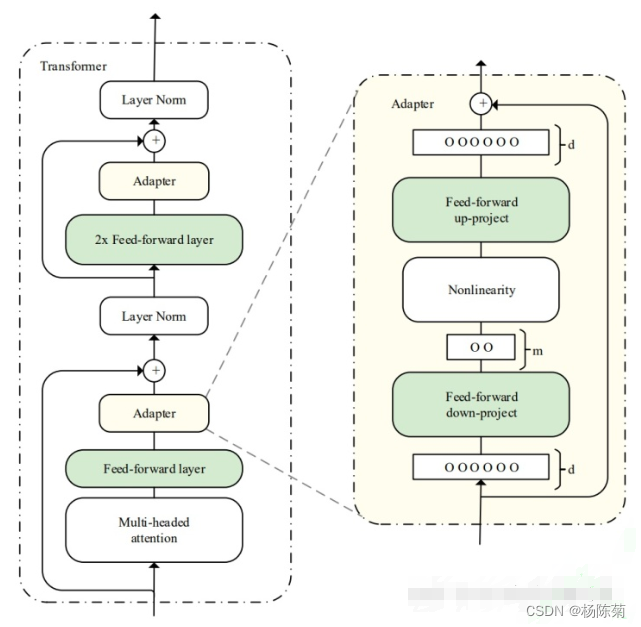
文章目录 微调方法Lora(在旁边添加训练参数)Adapter(在前面添加训练参数)Prefix-tuning(在中间添加训练参数)Prompt tuning PEFTPEFT 使用PeftConfigPeftModel保存和加载模型 微调方法
现流行的微调方法有:Lora,promp…


![[CISCN 2019初赛]Love Math - RCE(异或绕过)](https://img-blog.csdnimg.cn/8bbd59700b63463a9b931699b17484c1.png#pic_center)