系列文章目录

第一章 Python 机器学习入门之线性回归
第一章 Python 机器学习入门之梯度下降法
第一章 Python 机器学习入门之牛顿法

前言

上一篇文章里面说到了梯度下降法，它是使用泰勒近似定理保留一阶梯度并舍弃高阶梯度，那如果保留二阶梯度呢?这就是牛顿法的核心思想

一、牛顿法

1.牛顿法简介

用目标函数的二阶泰勒展开近似该目标函数，通过求解函数的极小值来求解凸优化的搜索方向；举个例子如果当前有个小球处于山谷中，想要最快地到达谷底，梯度下降法每次移动会找到坡度最大的方向，而牛顿法则不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大；

根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径；

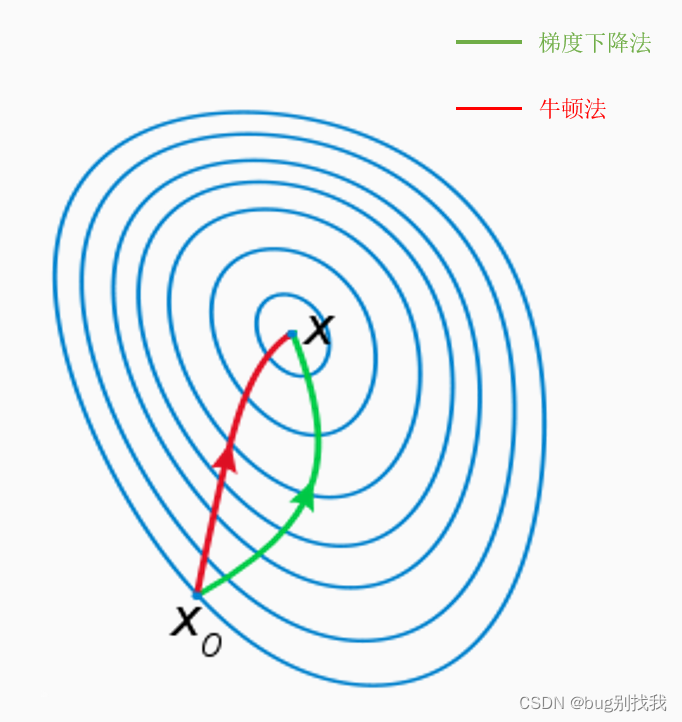
下图是两种方法到达谷底的路径图，可以明显看出牛顿法相比梯度下降法更快到达谷底，主要原因就是梯度下降法只考虑局部的最优解，而牛顿法往往从全局出发。

2.基本原理

我们还是用线性回归模型举例子，它的模型函数为

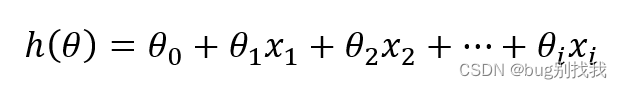
损失函数如下，h(x)为模型预测值，y为实际值，用平方误差函数用来判断损失

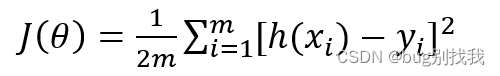
先对上述损失函数进行二阶泰勒展开，其中的g(𝜃_𝑛 )又称雅克比矩阵，H(𝜃_𝑛 )又称海森矩阵

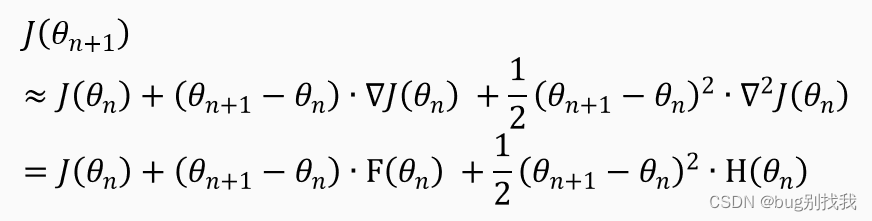
牛顿法的关键思想就在于它希望下一步就是最优解或者极值，也是说𝐽(𝜃_(𝑛+1) )等于极小值，那想要满足这种情况需要以下两个条件

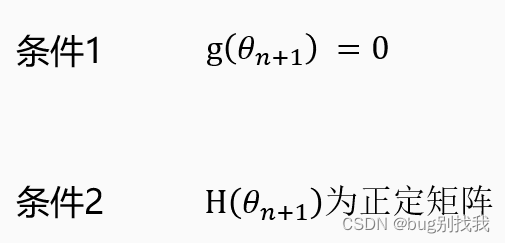
条件一g(𝜃_(𝑛+1) )=0 就是我们推导牛顿法式子的关键所在，我们知道想要满足如果下一步损失函数值为极值的条件，它所在位置的一阶梯度应该为0，注意这是一个必要条件，它不能确保下一步一定能到达极值点，但如果没有它就不可能到达极值点，因此我们对二阶泰勒展开式子两边进行求导得出下列解

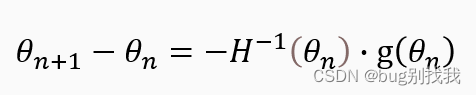
模型参数𝜃就沿着该方向移动到达下一位置即可，而该方向又被成为牛顿方向，牛顿法是没有步长这一概念的，因为它每一步都是当前状态下所能走出的最大步长，不需要我们人为设置；

我们再来说说条件二，从条件一我们知道每步移动的方向，但是什么时候能找到极小值或者最小值呢，我们就需要条件二了，将上述泰勒公式转为矩阵形式如下

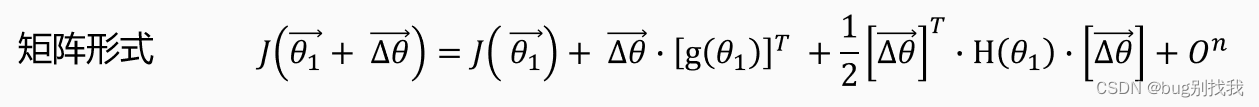
已知g(𝜃_(𝑛+1) )=0，𝐽((𝜃_1 ) ⃗+ (∆𝜃) ⃗ )和𝐽( (𝜃_1 ) ⃗ )的差值就由下式决定，它本质就是判断H(𝜃_1)是否是正定矩阵，相关知识可以搜索线代正定矩阵

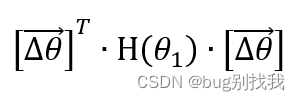
我们可以得出以下结论

如果满足条件二，函数只需一步就可以得到极值，相比梯度下降法会快很多；然而大多数情况下，我们往往遇到的都是第三种不确定的情况，这就要需要新的优化方法来解决，也就是拟牛顿法，该方法我们下次再讲。

总结

上述文章内容如果存在错误，欢迎大家批评指正！！！