线性数据结构集会

序言

一、数组

数组的优点

数组的缺点

数组的适用场景

二、链表

链表的优点

链表的缺点

链表的使用场景

链表的种类

Java单向链表的实现

三、队列

队列的特点

四、栈

栈的特点

栈的适用场景

五、时间复杂度简述

序言

线性数据结构是一种将数据元素以线性的方式组织和存储的数据结构。线性数据结构中的元素按顺序排列，每个元素最多只有一个前驱和一个后继。

常见的线性数据结构包括：

数组（Array）：连续存储相同类型的元素，通过索引直接访问。
链表（Linked List）：通过指针连接的节点组成，每个节点包含数据和指向下一个节点的指针。
栈（Stack）：具有先进后出（LIFO）特性，只能在栈顶进行插入和删除操作。
队列（Queue）：具有先进先出（FIFO）特性，只能在队尾进行插入，在队头进行删除。

一、数组

数组用于存储一组相同类型的元素。它是由连续的内存空间组成的，每个元素都有唯一的索引，使得可以通过索引访问和修改数组中的元素。

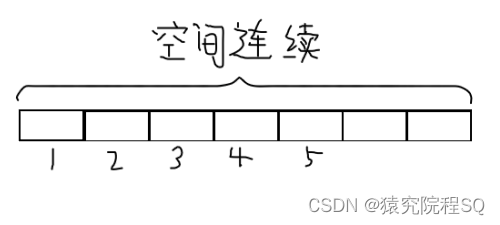
数组的优点

支持随机访问，因为数组的每个元素都有唯一索引；
占用内存较少，因为数组的元素连续存储，不需要额外的指针连接节点或元素之间的关系。
已知下标的插入删除可以快速精准定位

数组的缺点

当需要存储元素数量变化较大的情况时，需要重新分配更大的数组并进行数据复制，会造成一定的损失。
插入和删除效率低。对于需要在数组中间或开头插入或删除元素的操作，需要移动大量元素来保持连续性，造成插入和删除效率较低。
容易造成空间的浪费。

数组的适用场景

读多，修改少的时候
存储元素数量（长度）固定，数据变动很小的时候
需要存储简单且数量较小的数据的时候
通过数组顺序实现其他复杂数据结构的时候

二、链表

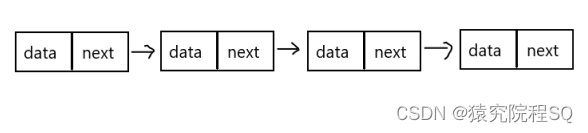
链表是由一系列节点组成，每个节点包含数据和指向下一个节点的指针。链表中的节点可以在内存中分散存储，彼此通过指针连接起来。

每个节点由两个主要部分组成：

数据：节点中存储的数据，可以是任意类型，根据具体需求而定。
指针：指向下一个节点的指针，通常称为"next"指针。它存储了下一个节点在内存中的地址或引用。

链表的第一个节点称为头节点，最后一个节点称为尾节点。尾节点的指针通常为null或空，表示链表的结束。

链表的优点

链表是通过指针的指向来实现线性连接的，不受固定大小的限制，空间利用率高。
插入和删除操作效率高，只需要修改前驱和后继节点的指向
灵活性高，适用于那些需要频繁修改结构的场景。

链表的缺点

查询效率低，因为它不能精准查询，需要遍历链表
内存消耗较高，一个节点不仅要存储数据本身，还要存储节点关系
存储不连续，无法充分利用缓存。

链表的使用场景

数据插入和删除频繁的场景
数据规模不确定的场景
通过链表链式实现其他复杂数据结构，比如树的链式存储。

链表的种类

链表的种类概述
链表类型	链表特点
单向链表（Singly Linked List）：每个节点包含一个指向下一个节点的指针。它是最简单的链表类型，适用于顺序访问以及插入和删除操作频繁的场景。	每个节点只包含一个指向下一个节点的指针。可以顺序访问节点。插入和删除操作的效率较高。查找某个节点的效率较低，需要从头节点开始逐一向后遍历
双向链表（Doubly Linked List）：每个节点包含一个指向下一个节点和一个指向前一个节点的指针。相比单向链表，双向链表可以双向访问，方便在某个节点之前或之后插入或删除节点。	每个节点包含一个指向下一个节点和一个指向前一个节点的指针。可以双向访问节点，不仅可以从头到尾遍历，还可以从尾到头遍历。插入和删除操作更加灵活，可以在某个节点之前或之后插入或删除节点。链表的结构相对复杂，需要额外的指针来维护前后节点的关系。
循环链表（Circular Linked List）：和单向链表或双向链表类似，不同之处在于最后一个节点的指针指向第一个节点，形成一个循环。循环链表的一个优点是在操作时更容易处理边界情况，因为没有"尾部"节点。	和单向链表或双向链表类似，最后一个节点的指针指向第一个节点，形成一个循环。可以用于处理环形相关问题，比如判断链表中是否存在环。需要额外注意循环的终止条件，以防止陷入无限循环。
跳表（Skip List）：跳表是一种有序链表的扩展，通过在不同层级上添加额外的指针，使得搜索的效率更高。跳表可以用于需要高效搜索和插入操作的场景，比如有序集合的实现。	是一种有序链表的扩展，通过在不同层级上添加额外的指针，提高搜索的效率。可以用于高效的搜索和插入操作，适用于需要快速定位的有序集合场景。需要额外的空间来维护层级指针，占用较多的存储空间。

Java单向链表的实现

package com.csq;

import java.util.StringJoiner;

import com.practice.SingleLinked.Node;

// 链表类
public class Linked<E> {
	
	// 头结点
	private Node<E> first;
		
	// 尾节点
	private Node<E> last;
	
	// 头插法
	public void addFirst(E item) {
		// 新节点
		final Node<E> newNode = new Node<E>(item);
		// 保存原来的头节点
		final Node<E> f = first;
		// 新的节点变成新的头节点
		first = newNode;
		// 如果原头节点不为空,即链表不为空
		if(f != null) {
			// 新头节点的下一个节点指向原头节点
			newNode.next = f;
		}else {
			// 如果链表为空,新节点既是头节点也是尾节点
			last = newNode;
		}
		
	}
	
	// 尾插法
	public void addLast(E item) {
		// 创建新节点
		final Node<E> newNode = new Node<E>(item);
		// 保存原来的尾节点
		final Node<E> l = last;
		// 新节点变为新的尾节点
		last = newNode;
		// 链表为空
		if(l == null) {
			// 既是头节点也是尾节点
			first = newNode;
		}else {
			l.next = newNode;
		}
		
	}
	
	//获取链表长度
	public int size() {
		int size = 0;
		for (Node<E> x = first; x != null; x = x.next) {
			size++;
		}
		return size;
	}

	// 重写toString()输出链表结果
	@Override
	public String toString() {
		/* StringJoiner类是用于拼接字符串的辅助类。
		 * 用于将多个字符串按照指定的分隔符连接起来，生成一个新的字符串。*/
		StringJoiner sj = new StringJoiner("->");
		for(Node<E> n = first; n!= null;n=n.next) {
			sj.add(n.item.toString());
		}
		return sj.toString();
	}
	
	// 单向链表的节点
	public static class Node<E>{
		E item; // 数据域
		Node<E> next; // 后继节点(指针域)
		public Node(E data) {
		    this.item = data;
		}
	}
}

三、队列

队列是一种常见的数据结构，它按照先进先出（FIFO）的原则管理数据。队列有两个基本操作：入队（enqueue）和出队（dequeue）。

队列可以简单地定义为具有以下属性的数据集合：

队尾（rear）：用于插入新元素的位置。
队头（front）：用于删除元素的位置，也是队列中最早插入的元素。

当元素按顺序插入队列时，它们按照先进先出的顺序删除。新元素始终插入队列的队尾，而删除操作始终在队头进行。

队列可以使用数组或链表实现。数组实现的队列称为顺序队列，链表实现的队列称为链式队列。

队列的特点

先进先出(FIFO)：队列按照元素的插入顺序进行处理，保证了先进入队列的元素先被处理。
顺序性：队列可以维护元素的顺序，适用于那些需要按照特定顺序进行处理的场景。
简单高效：队列的插入和删除操作只涉及到队头和队尾，具有较高的执行效率。

队列适用于需要按照先进先出顺序处理任务、保持顺序性、实现并发和协作等场景。

四、栈

栈（Stack）是一种具有特定操作规则的线性数据结构，它按照后进先出（Last-In-First-Out，LIFO）的原则进行操作。栈可以看作是一种受限制的线性表，只允许在表的一端进行插入和删除操作，这一端被称为栈顶，另一端称为栈底。

栈的定义可以用以下几个要点来描述：

数据存储：栈中的元素按照一定的顺序存储，通常使用数组或链表来实现。
后进先出：栈的特点是在进行插入（压栈）和删除（弹栈）操作时，最后一个插入的元素首先被删除。
只操作栈顶：栈的操作限制只能在栈顶进行，也即只允许从栈顶插入和删除元素。
是一个有限容量的容器：存储元素的数量有限，当栈满时无法再插入新的元素。栈空时，无法弹出元素。

在栈中，插入新的元素（压栈）会将元素放置在当前栈顶上方，而删除元素（弹栈）会将栈顶元素移除并返回该元素。此外，栈还提供了一个方法用于读取当前栈顶元素的值，而不对栈进行修改。

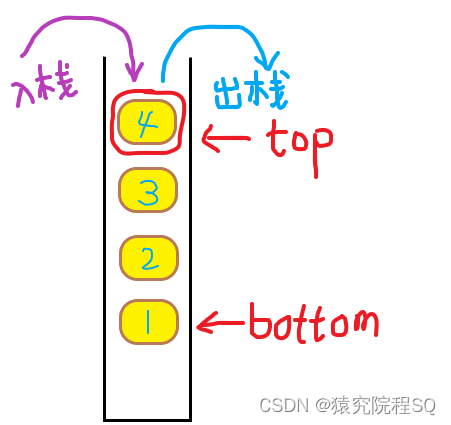
栈的特点

后进先出（Last-In-First-Out，LIFO）：栈的操作原则是先插入的元素将最后一个被删除。也就是说，最后压入（插入）栈的元素将成为下一个弹出（删除）的元素。
只操作栈顶：栈操作只涉及栈顶元素的插入、删除和读取，不允许直接访问或修改栈中的其他元素。
有限容量：栈的容量是有限的，即在一个栈中可以存储的元素数量是有限的。
快速插入和删除：由于栈的特性，插入（压栈）和删除（弹栈）操作都只需在栈顶进行，时间复杂度为 O(1)。这使得栈在对数据进行临时存储和后续操作时非常高效。
存储顺序：栈中的元素按照插入顺序存储，后插入的元素位于较早插入的元素之上。栈的顶部视为最新插入的元素，栈底视为最早插入的元素。