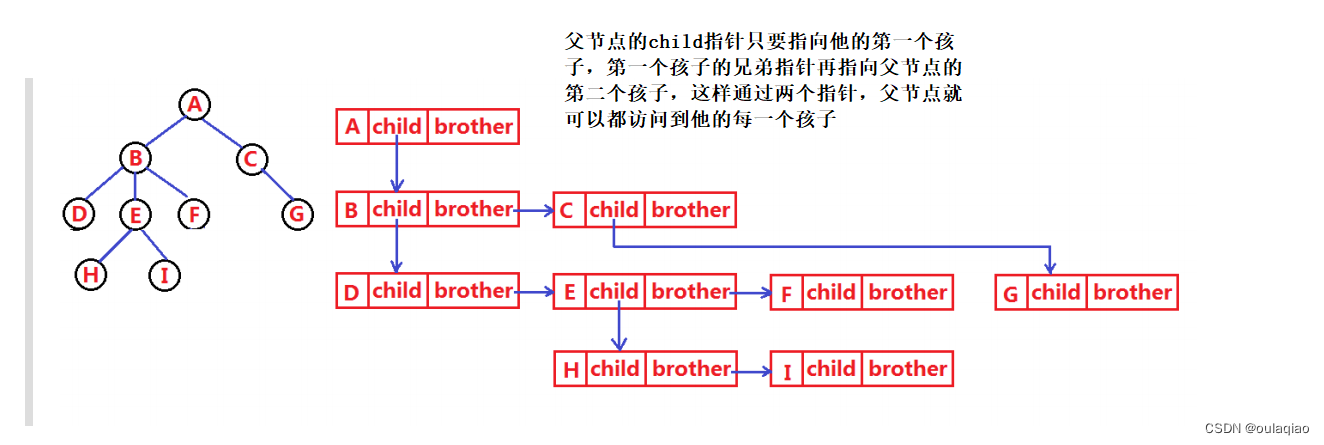
最开始接触树的时候，因为并不是二叉树，所以我们并不知道一个节点最多有几个度，所以我们要用链表来实现树的话就需要用孩子兄弟法

然后我们认识了完全二叉树，因为它是从左到右都满的二叉树，所以我们可以用顺序表（数组）来存储

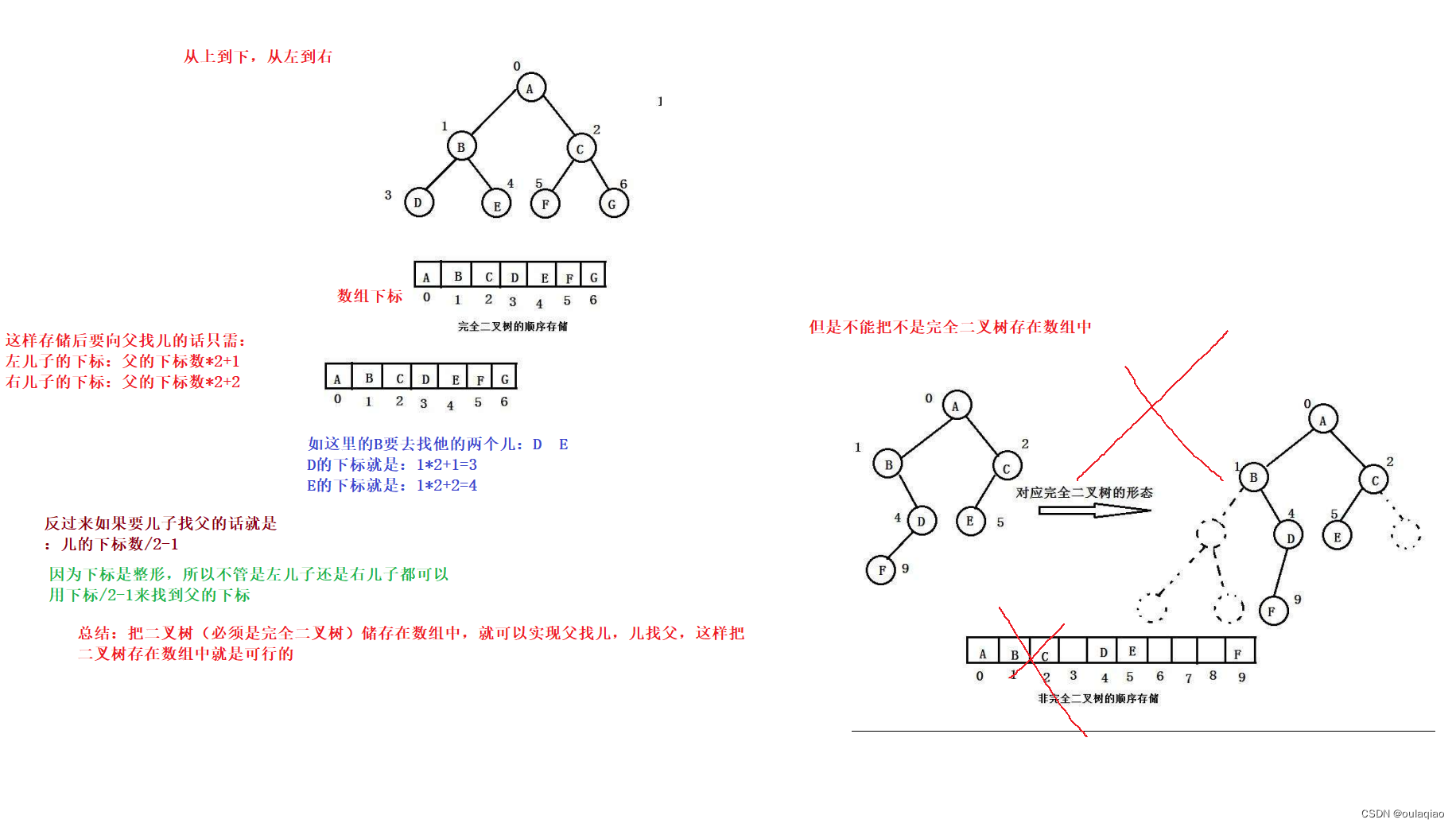
但是如果不是完全二叉树的话，用顺序表储存的话就不好，那么又因为他是二叉树了，一个节点做多只有两个度，所以可以用一个结构体（里面包含两个结构体指针，和储存在节点的数）来表示二叉树中的每个节点

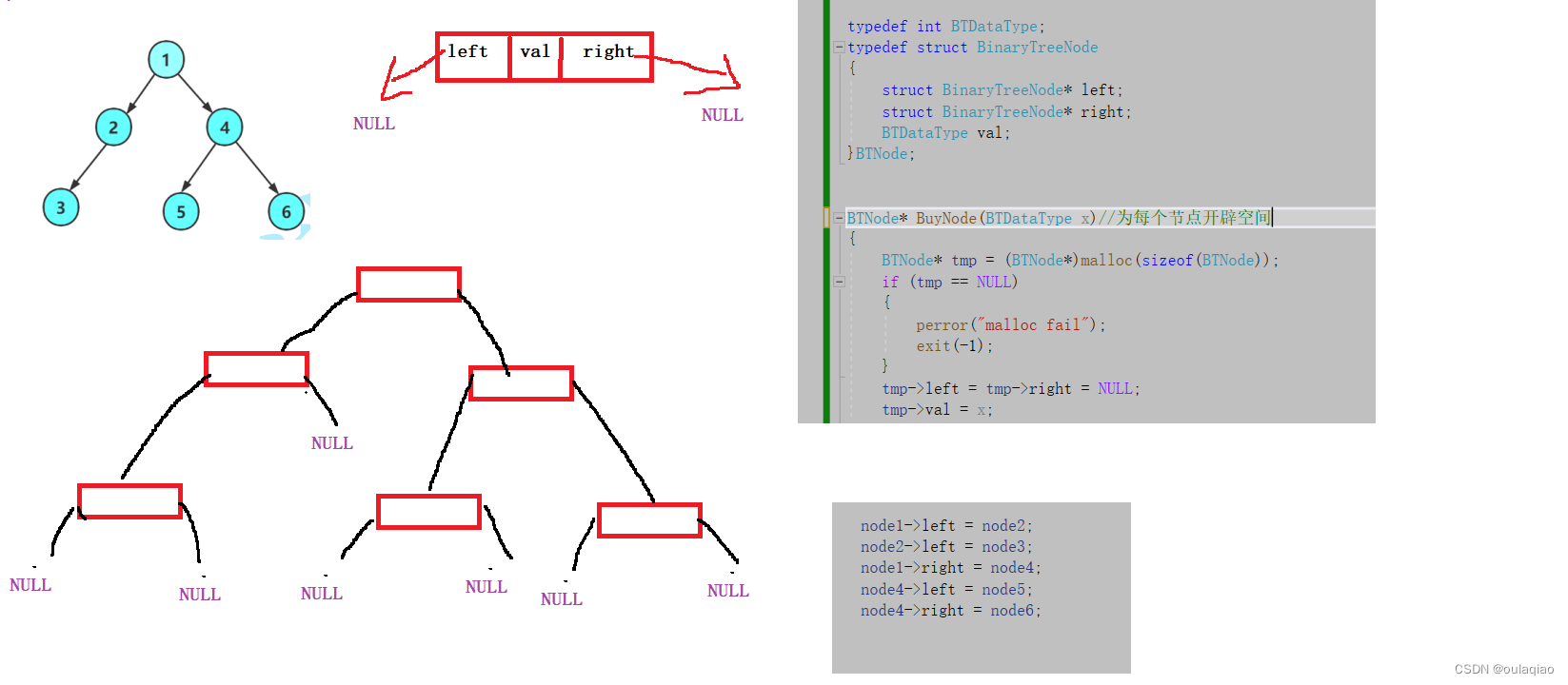
上述代码并不是创建二叉树的方式，现在我们只是手动弄出一个二叉树，方便之后对他结构实现的运用
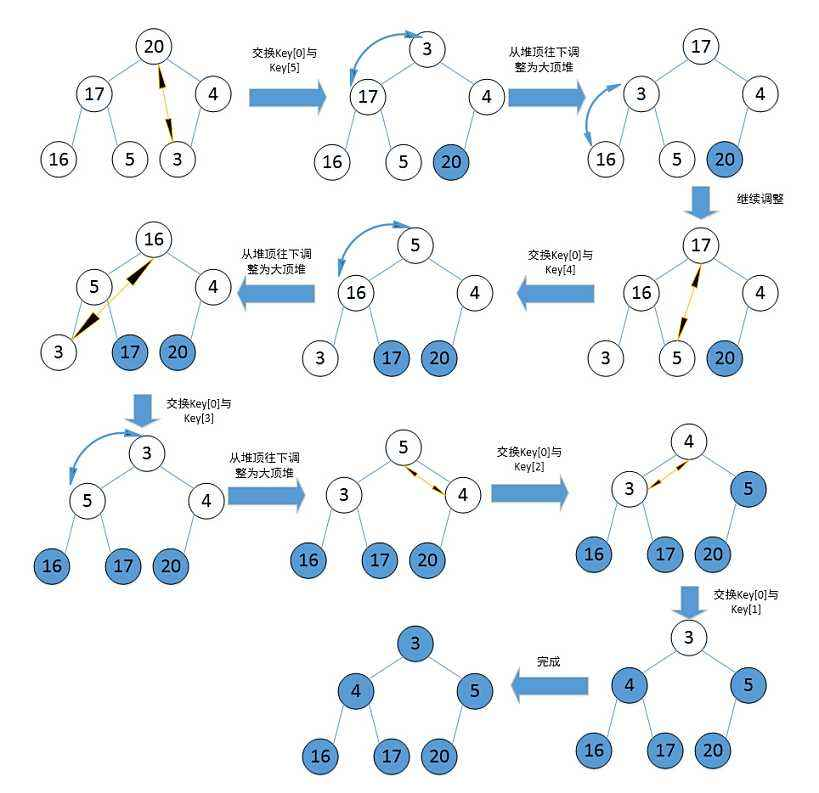
我们可以把二叉树的每一个子，够看成有，根左子树，右子树。所以二叉树的遍历是递归的

现在我们用代码来实现这三中二叉树的遍历（递归）
前序遍历：

void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->val);
	PreOrder(root->left);
	PreOrder(root->right);
}

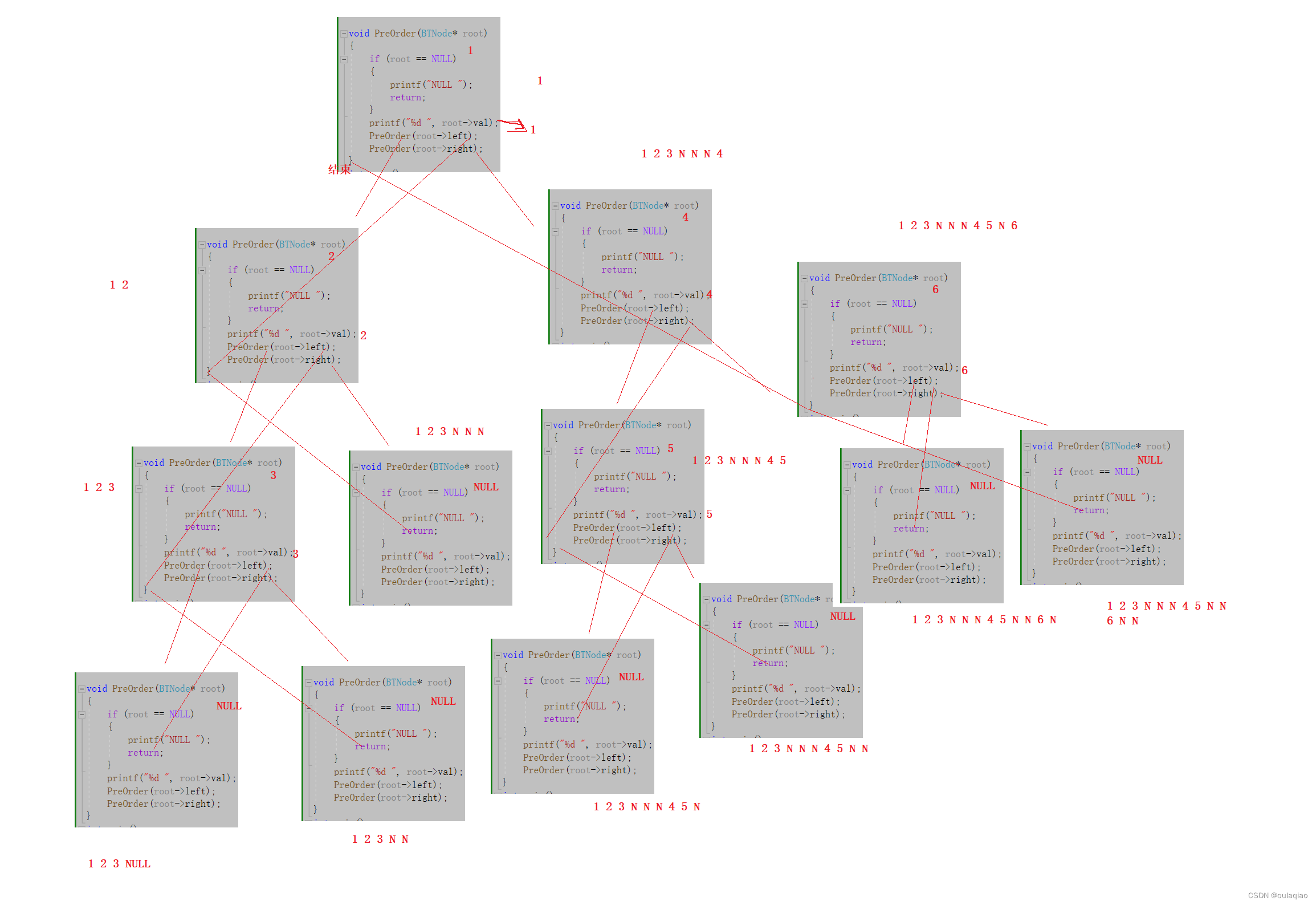
同样的原理——中序遍历：

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->val);
	InOrder(root->right);
}

同样的原理——后序遍历：

void PostOrder(BTNode* root)
{

	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->val);

}

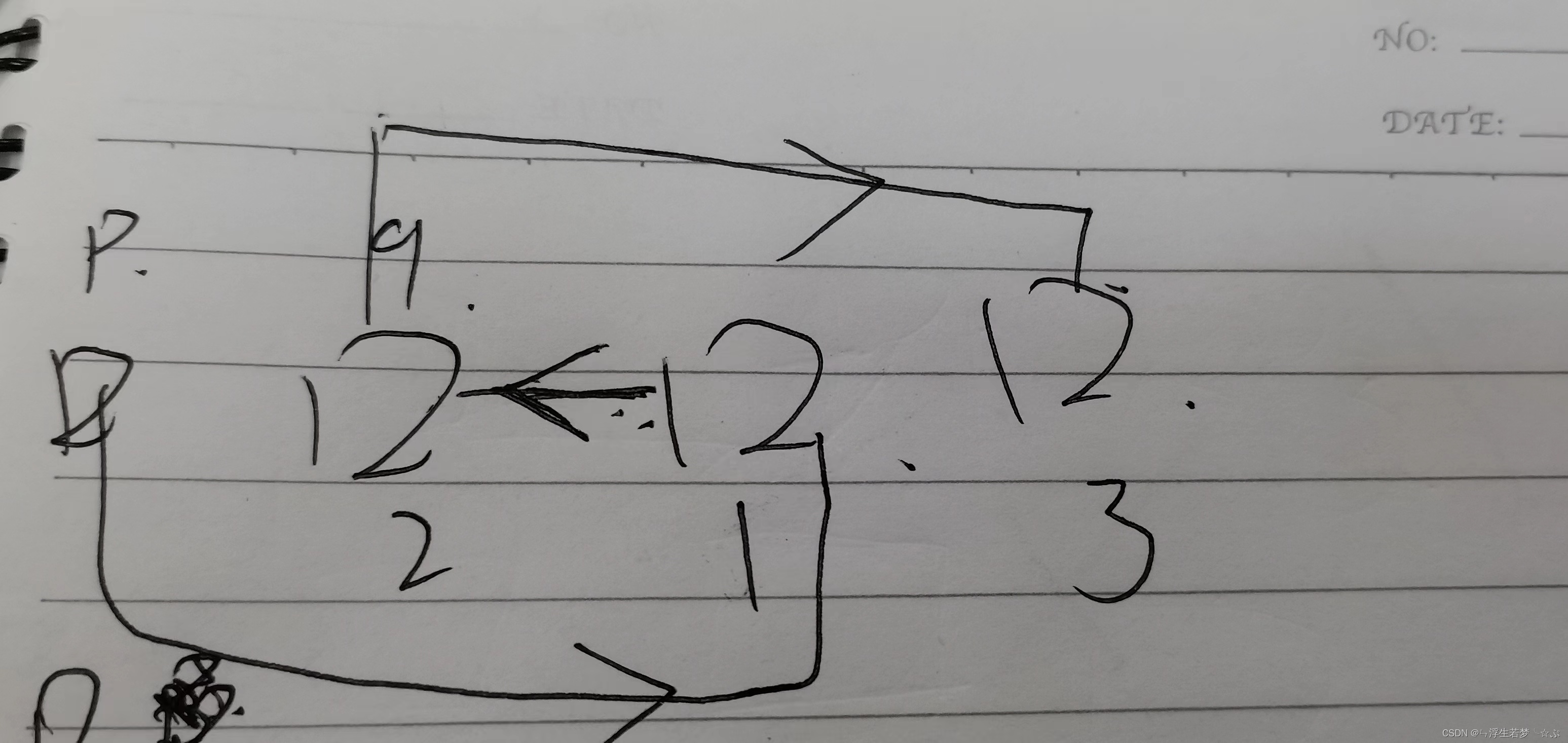
前
中
后
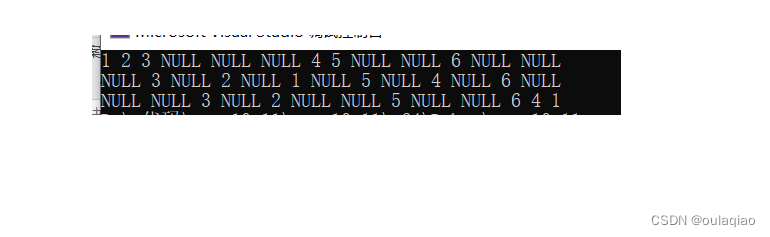
打印的结果：

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType val;
}BTNode;


BTNode* BuyNode(BTDataType x)//为每个节点开辟空间
{
	BTNode* tmp = (BTNode*)malloc(sizeof(BTNode));
	if (tmp == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	tmp->left = tmp->right = NULL;
	tmp->val = x;
}

void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->val);
	PreOrder(root->left);
	PreOrder(root->right);
}
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->val);
	InOrder(root->right);
}

void PostOrder(BTNode* root)
{

	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->val);

}
int main()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node2->left = node3;
	node1->right = node4;
	node4->left = node5;
	node4->right = node6;

	// 二叉树前序遍历
	PreOrder(node1);
	// 二叉树中序遍历
	printf("\n");
	InOrder(node1);
	printf("\n");

	// 二叉树后序遍历
	 PostOrder(node1);

}