21字符串-简单操作

news2024/9/21 4:25:07

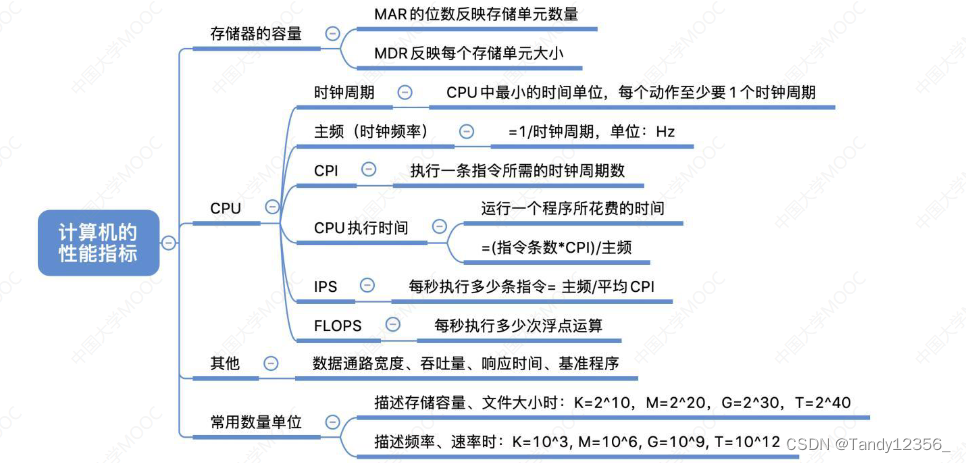
字符串匹配

重要概念

BF算法

RK算法

LeetCode之路——344. 反转字符串

分析

LeetCode之路——541. 反转字符串 II

分析

字符串匹配

字符串匹配的算法很多，常见的有BF（Brute Force）、RK（Rabin-Karp）这两种比较简单、好理解的，当然也有BM（Boyer-Moore）和KMP（Knuth Morris Pratt）这两种比较难理解、更高效的。

重要概念

在字符串匹配中，有两个需要了解的概念——主串和模式串。比如说我们需要在字符串N中查找字符串M,那么N就是主串，M就是模式串。主串的长度如果记为n，模式串长度记为m，所以n>m。

BF算法

BF算法主打一个暴力匹配。举例说明：在字符串anbdbanc中查找anc。

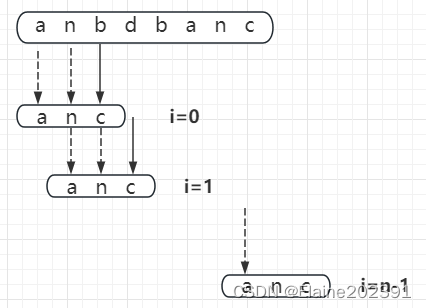
BF算法极端情况下，我们每次都需要比对m个字符，要比对n-m+1次，算法的最坏情况时间复杂度是O(n*m)。

RK算法

是由两位发明者Rabin和Karp的名字命名的，可以理解为BF的升级版。

RK是基于哈希值的基础上进行比较的，我们知道主串中一共有n-m+1个子串，我们只需要计算出每个子串的哈希值，然后与模式串的哈希值比较，如果相等就是相同的。

假设a-z总计26个字母分别用1-24表示，对应的子串用26进制表示哈希值。

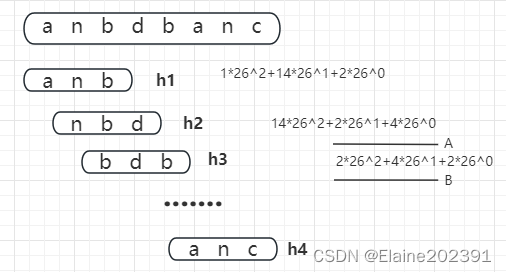
A和B是相邻两个子串相同部分，可以知道B = 26 * A。从这里例子中，我们很容易就能得出这样的规律：

相邻两个子串s[i-1]和s[i]（i表示子串在主串中的起始位置，子串的长度都为m），对应的哈希值计算公式有交集，也就是说，我们可以使用s[i-1]的哈希值很快的计算出s[i]的哈希值。如果用公式表示的话，就是下面这个样子(h[i-1]对应子串S[i-1,i+m-2]的哈希值，h[i]对应子串S[i,I+m-1]的哈希值)：

h[i]=26*(h[i-1]-26^(m-1)*s[i-1])+s[i+m-1]

以h2和h3举例，h[i-1]-26^(m-1)*s[i-1]就是A，h[i] = A * 26 + s[i+m-1],其中s[i-1]是h2中的n,s[i+m-1]是h3中的b。我们可以提前用长度为m的数组存放26的0到m次方，省去计算的时间。

整个RK算法包含两部分，计算子串哈希值和模式串哈希值与子串哈希值之间的比较。

第一部分，我们前面也分析了，可以通过设计特殊的哈希算法，只需要扫描一遍主串就能计算出所有子串的哈希值了，所以这部分的时间复杂度是O(n)。
模式串哈希值与每个子串哈希值之间的比较的时间复杂度是O(1)，总共需要比较n-m+1个子串的哈希值，所以，这部分的时间复杂度也是O(n)。所以，RK算法整体的时间复杂度就是O(n)。

暂时先介绍这两种算法，练练手应该能够了。

LeetCode之路——344. 反转字符串

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

示例 1：

输入：s = ["h","e","l","l","o"]
输出：["o","l","l","e","h"]

示例 2：

输入：s = ["H","a","n","n","a","h"]
输出：["h","a","n","n","a","H"]

提示：

1 <= s.length <= 105
s[i] 都是 ASCII 码表中的可打印字符

分析

熟悉双指针的情况下，会很自然的想到首尾两指针向中间移动，一边遍历一边交换的解决方案。

class Solution {
    public void reverseString(char[] s) {
        for (int h = 0, t = s.length - 1; h < t; ++h, --t) {
            char tmp = s[h];
            s[h] = s[t];
            s[t] = tmp;
        }
    }
}

时间复杂度：O(n)
空间复杂度：O(1)

LeetCode之路——541. 反转字符串 II

给定一个字符串 s 和一个整数 k，从字符串开头算起，每计数至 2k 个字符，就反转这 2k 字符中的前 k 个字符。

如果剩余字符少于 k 个，则将剩余字符全部反转。
如果剩余字符小于 2k 但大于或等于 k 个，则反转前 k 个字符，其余字符保持原样。

示例 1：

输入：s = "abcdefg", k = 2
输出："bacdfeg"

示例 2：

输入：s = "abcd", k = 2
输出："bacd"

提示：

1 <= s.length <= 104
s 仅由小写英文组成
1 <= k <= 104

分析

就直接按照题意来，反转每个下标从2k的倍数开始的，长度为k的子串。若该子串长度不足k，则反转整个子串。

class Solution {
    public String reverseStr(String s, int k) {
        //定义一个表示字符串的长度的变量
        int len =s.length();
        //将字符串变为字符数组，方便当个字符遍历
        char[] chars= s.toCharArray();
        for(int left = 0; left<len; left +=2*k){
            //左指针是为了定义反转位置的开始，右指针定义反转位置的结束。
            //特别备注下，这边的Math.min()起到的作用是，字符小于k时，全部反转的效果。
            //当k>len的时候，就取len。
            reverse(chars, left, Math.min(left+k,len)-1);
        }
        //返回结果
        return new String(chars);
    }
    public void reverse(char[] chars, int left, int rigth){
        //只要左指针小于右指针就反转
        //这边是为了兼容处理 k >len情况下，将所有字符都反转
        while(left <rigth){
            char temp = chars[left];
            chars[left] =chars[rigth];
            chars[rigth] = temp;
            //左指针向右移动
            left++;
            //右指针向左移动
            rigth--;
        }
    }
}