RNN/LSTM学习记录

一.RNN

什么是循环神经网络：

循环神经网络，从名字上理解“循环”，即为构成一个往复的结构，它有着这样的特点，对时序特征的数据十分敏感，能够挖掘出数据中的书序信息以及语义信息。

什么是序列特性呢，就是符合时间顺序，或者其他顺序就叫做序列特性。举个例子就是

拿人类的某句话来说，也就是人类的自然语言，是不是符合某个逻辑或规则的字词拼凑排列起来的，这就是符合序列特性。
语音，我们发出的声音，每一帧每一帧的衔接起来，才凑成了我们听到的话，这也具有序列特性、
股票，随着时间的推移，会产生具有顺序的一系列数字，这些数字也是具有序列特性。

为什么要发明循环神经网络：

我们先来看一个NLP很常见的问题，命名实体识别，举个例子，现在有两句话：

第一句话：I like eating apple！（我喜欢吃苹果！）

第二句话：The Apple is a great company！（苹果真是一家很棒的公司！）

现在的任务是要给apple打Label，我们都知道第一个apple是一种水果，第二个apple是苹果公司，假设我们现在有大量的已经标记好的数据以供训练模型，当我们使用全连接的神经网络时，我们做法是把apple这个单词的特征向量输入到我们的模型中（如下图），在输出结果时，让我们的label里，正确的label概率最大，来训练模型，但我们的语料库中，有的apple的label是水果，有的label是公司，这将导致，模型在训练的过程中，预测的准确程度，取决于训练集中哪个label多一些，这样的模型对于我们来说完全没有作用。问题就出在了我们没有结合上下文去训练模型，而是单独的在训练apple这个单词的label，这也是全连接神经网络模型所不能做到的，于是就有了我们的循环神经网络。

循环神经网络的结构及原理：

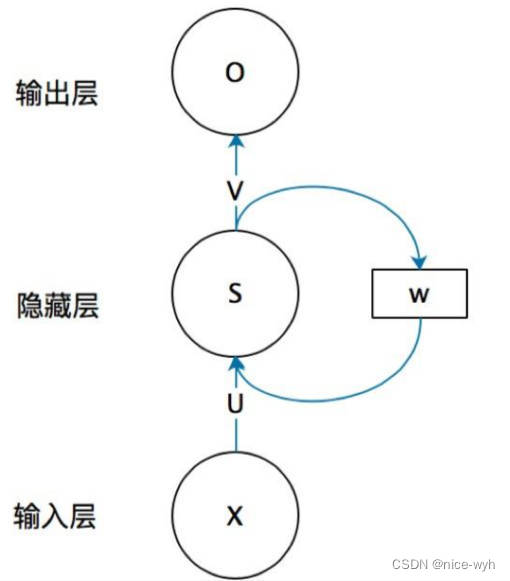
上图就是RNN的结构，我第一次看到这图的第一反应是，不是说好的循环神经网络么，起码得是神经网络啊，神经网络不是有很多球球么，也就是神经元，这RNN咋就这几个球球，不科学啊，看不懂啊！！！！随着慢慢的了解RNN，才发现这图看着是真的清楚，因为RNN的特殊性，如果展开画成那种很多神经元的神经网络，会很麻烦。

首先不要管右边的W，只看X,U,S,V,O，这幅图就变成了，如下

等等，这图看着有点眼熟啊，这不就是全连接神经网络结构吗？对，没错，不看W的话，上面那幅图展开就是全连接神经网络，其中X是一个向量，也就是某个字或词的特征向量，作为输入层，如上图也就是3维向量，U是输入层到隐藏层的参数矩阵，在上图中其维度就是3X4，S是隐藏层的向量，如上图维度就是4，V是隐藏层到输出层的参数矩阵，在上图中就是4X2，O是输出层的向量，在上图中维度为2。有没有一种顿时豁然开朗的感觉，正是因为我当初在学习的时候，可能大家都觉得这个问题比较小，所以没人讲，我一直搞不清楚那些神经元去哪了。。所以我觉得讲出来，让一些跟我一样的小白可以更好的理解。

弄懂了RNN结构的左边，那么右边这个W到底是什么啊？把上面那幅图打开之后，是这样的：

等等，这又是什么？？别慌，很容易看，举个例子，有一句话是，I love you，那么在利用RNN做一些事情时，比如命名实体识别，上图中的 Xt−1 代表的就是I这个单词的向量，X代表的是love这个单词的向量， Xt+1 代表的是you这个单词的向量，以此类推，我们注意到，上图展开后，W一直没有变，W其实是每个时间点之间的权重矩阵，我们注意到，RNN之所以可以解决序列问题，是因为它可以记住每一时刻的信息，每一时刻的隐藏层不仅由该时刻的输入层决定，还由上一时刻的隐藏层决定，公式如下，其中Qt 代表t时刻的输出, St 代表t时刻的隐藏层的值：

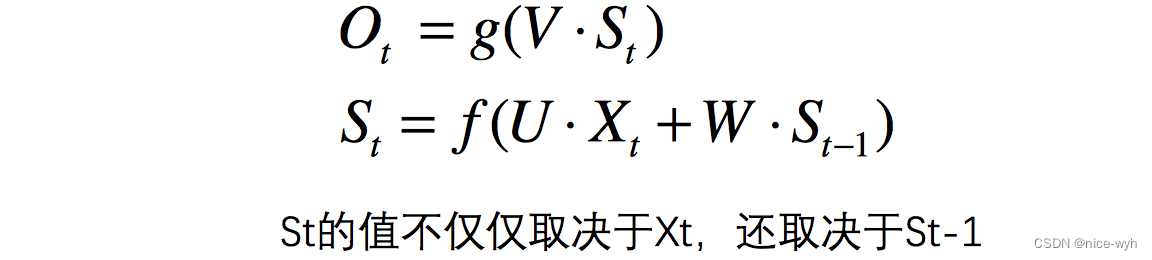
值得注意的一点是，在整个训练过程中，每一时刻所用的都是同样的W。

举个例子，方便理解

假设现在我们已经训练好了一个RNN，如图，我们假设每个单词的特征向量是二维的，也就是输入层的维度是二维，且隐藏层也假设是二维，输出也假设是二维，所有权重的值都为1且没有偏差且所有激活函数都是线性函数，现在输入一个序列，到该模型中，我们来一步步求解出输出序列：

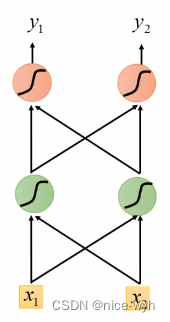
你可能会好奇W去哪了？W在实际的计算中，在图像中表示非常困难，所以我们可以想象上一时刻的隐藏层的值是被存起来，等下一时刻的隐藏层进来时，上一时刻的隐藏层的值通过与权重相乘，两者相加便得到了下一时刻真正的隐藏层，如图 a1 , a2 可以看做每一时刻存下来的值，当然初始时a1 , a2是没有存值的，因此初始值为0：

当我们输入第一个序列，【1,1】，如下图，其中隐藏层的值，也就是绿色神经元，是通过公式St = f(U * Xt + W * St-1) 计算得到的，因为所有权重都是1，所以也就是 1∗1+1∗1+1∗0+1∗0=2 （我把向量X拆开计算的，由于篇幅关系，我只详细列了其中一个神经元的计算过程，希望大家可以看懂，看不懂的请留言），输出层的值4是通过公式 Qt=g(V⋅St) 计算得到的，也就是 2∗1+2∗1=4 （同上，也是只举例其中一个神经元），得到输出向量【4,4】：

当【1,1】输入过后，我们的记忆里的 a1,a2 已经不是0了，而是把这一时刻的隐藏状态放在里面，即变成了2，如图，输入下一个向量【1,1】，隐藏层的值通过公式St=f(U * Xt + W * St−1) 得到， 1∗1+1∗1+1∗2+1∗2=6 ，输出层的值通过公式Qt=g(V * St)，得到 6∗1+6∗1=12 ，最终得到输出向量【12,12】：

同理，该时刻过后 a1,a2 的值变成了6，也就是输入第二个【1,1】过后所存下来的值，同理，输入第三个向量【2,2】，如图，细节过程不再描述，得到输出向量【32,32】：

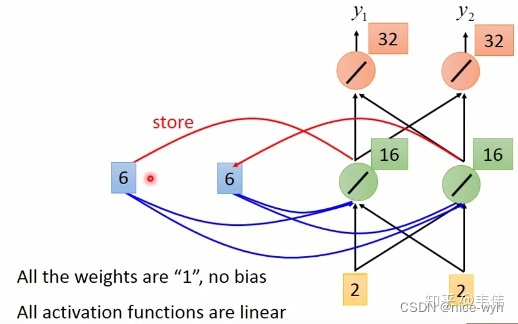
由此，我们得到了最终的输出序列为

至此，一个完整的RNN结构我们已经经历了一遍，我们注意到，每一时刻的输出结果都与上一时刻的输入有着非常大的关系，如果我们将输入序列换个顺序，那么我们得到的结果也将是截然不同，这就是RNN的特性，可以处理序列数据，同时对序列也很敏感。

二.LSTM

如果你经过上面的文章看懂了RNN的内部原理，那么LSTM对你来说就很简单了，首先大概介绍一下LSTM，是四个单词的缩写，Long short-term memory，翻译过来就是长短期记忆，是RNN的一种，比普通RNN高级（上面讲的那种），基本一般情况下说使用RNN都是使用LSTM，现在很少有人使用上面讲的那个最基础版的RNN，因为那个存在一些问题，LSTM效果好，当然会选择它了！

长短时记忆网络(Long Short Term Memory Network, LSTM)，是一种改进之后的循环神经网络，可以解决RNN无法处理长距离的依赖的问题，目前比较流行。

长短时记忆网络的思路：

原始 RNN 的隐藏层只有一个状态，即h，它对于短期的输入非常敏感。
再增加一个状态，即c，让它来保存长期的状态，称为单元状态(cell state)。

把上图按照时间维度展开

在 t 时刻，LSTM 的输入有三个：当前时刻网络的输入值、上一时刻 LSTM 的输出值、以及上一时刻的单元状态；
LSTM 的输出有两个：当前时刻 LSTM 输出值、和当前时刻的单元状态.

关键问题是：怎样控制长期状态 c ？

方法是：使用三个控制开关

第一个开关，负责控制继续保存长期状态c；
第二个开关，负责控制把即时状态输入到长期状态c；
第三个开关，负责控制是否把长期状态c作为当前的LSTM的输出

如何在算法中实现这三个开关？

方法：用门（gate）

定义：gate 实际上就是一层全连接层，输入是一个向量，输出是一个 0到1 之间的实数向量。
公式为：

回忆一下它的样子：

gate 如何进行控制？

方法：用门的输出向量按元素乘以我们需要控制的那个向量
原理：门的输出是 0到1 之间的实数向量，
当门输出为 0 时，任何向量与之相乘都会得到 0 向量，这就相当于什么都不能通过；
输出为 1 时，任何向量与之相乘都不会有任何改变，这就相当于什么都可以通过。

LSTM 前向计算

在 LSTM－1 中提到了，模型是通过使用三个控制开关来控制长期状态 c 的：

这些开关就是用门（gate）来实现：

接下来具体看这三重门

LSTM 的前向计算:

一共有 6 个公式

遗忘门（forget gate）
它决定了上一时刻的单元状态 c_t-1 有多少保留到当前时刻 c_t

输入门（input gate）
它决定了当前时刻网络的输入 x_t 有多少保存到单元状态 c_t

输出门（output gate）
控制单元状态 c_t 有多少输出到 LSTM 的当前输出值 h_t

遗忘门的计算为：

forget

遗忘门的计算公式中：
W_f 是遗忘门的权重矩阵，[h_t-1, x_t] 表示把两个向量连接成一个更长的向量，b_f 是遗忘门的偏置项，σ 是 sigmoid 函数。

输入门的计算：

input

根据上一次的输出和本次输入来计算当前输入的单元状态：

当前输入的单元状态c_t

当前时刻的单元状态 c_t 的计算：由上一次的单元状态 c_t-1 按元素乘以遗忘门 f_t，再用当前输入的单元状态 c_t 按元素乘以输入门 i_t，再将两个积加和：
这样，就可以把当前的记忆 c_t 和长期的记忆 c_t-1 组合在一起，形成了新的单元状态 c_t。
由于遗忘门的控制，它可以保存很久很久之前的信息，由于输入门的控制，它又可以避免当前无关紧要的内容进入记忆。