树的基本概念

• 树形结构中一个结点可以有一个或多个直接后继

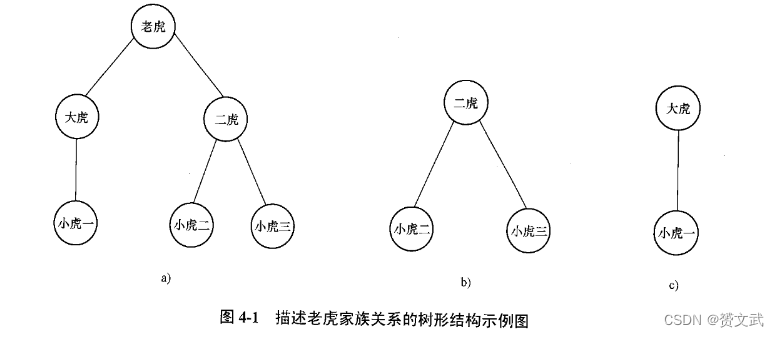
树的概念

• 树是n(n>=0)个结点的有限集合，一棵树满足以下两个条件：
  • 当n=0时，称为空树
  • 当n>0时，有且仅有一个称为根的结点，除根结点外 ，其余结点分为m(m>=0)个互不相交的非空集合，这些非空集合中的每一个都是一颗树，称为根的子树
• 森林：m个互不相交的树的集合。删除一个非空树的根结点，它的子树便构成森林

树的相关术语

• 结点的度：树上任何一个结点所拥有的子树数目称为该结点的度
• 叶子：度为0的结点称为叶子或终端结点
• 树的度：一棵树中所有结点的度的最大值称为该树的度
• 一个结点的子树的根称为该结点的孩子（或称子结点），相应该结点称为孩子的双亲（父结点）
• 结点的层次：从根开始算起，根为1，其余结点层次为其双亲的层次+1
• 树的高度：一棵树中所有结点层次数的最大值
• 有序树：各节点子树从左到右是有次序的，不能互换
• 无序树：各结点的子树是无次序的，可以互换，称为无序树
• 树的基本运算
  • 求根
  • 求双亲
  • 求孩子
  • 建树
  • 剪枝
  • 遍历

二叉树

二叉树基本概念

• 二叉树：n(n>=0)个元素的有限集合，该集合或为空，或由一根及两根互不相交的左子树和右子树组成
• 二叉树五种基本形态：

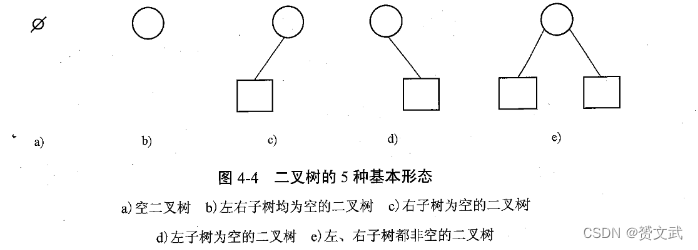
• 二叉树基本运算：
  • 初始化：建立一棵空二叉树
  • 求双亲：求出二叉树上结点XX的双亲结点
  • 求左孩子Lchild(BT,X)和求右孩子Rchild(BT,X)
  • 建二叉树
  • 先序遍历：先访问根节点，然后递归地访问左子树，最后递归地访问右子树。（根-左-右）
  • 中序遍历 ：先递归地访问左子树，然后访问根节点，最后递归地访问右子树。（左-根-右）
  • 后序遍历：先递归地访问左子树，然后递归地访问右子树，最后访问根节点。（左-右-根）
  • 层次遍历：从上到下逐层遍历二叉树的节点。

二叉树的性质

• 二叉树第i(i>=1)曾上至多有2^i-1个结点
• 深度为k(k>=1)的二叉树至多有2^k-1个结点
• 对于任何一颗二叉树，若度数为0的结点个数为n₀,度数为2的结点个数为n₂,则n₀=n₂+!

注：深度为k(k>=1)且有2^k-1个结点的二叉树称为满二叉树；完全二叉树：对满二叉树从上到下，从左到右顺序编号，并在最下层删除部分结点，如果删除的这些结点的编号是连续的且删除的结点中含有最大编号的结点，那么这棵二叉树是完全二叉树

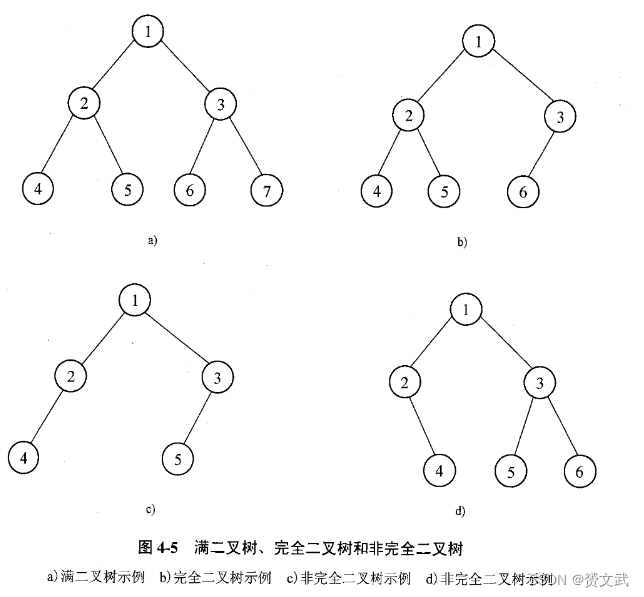
• 含有n个结点的完全二叉树的深度为⌊log₂n⌋+1(⌊⌋符号表示向下取整)
• 如果将一棵有n个结点的完全二叉树按层编号，将一棵二叉树的所有n个结点按从第一层到最大层，每层从左到右依次编号，则对任一编号为i(1<=i<=n)的结点A有：
  • 若i=1,则结点A是根；若i>1,则A的双亲Parent(A)的编号为⌊i/2⌋
  • 若2i>n,则结点A既无左孩子，也无右孩子；否则A的左孩子Lchild(A)的编号为2i+1
  • 若2i+1>n,则结点A无右孩子；否则，A的右孩子Rchild(A)的编号为2i+1

二叉树的存储结构

二叉树的顺序存储结构

• 二叉树的 顺序存储结构可以用一维数组来实现

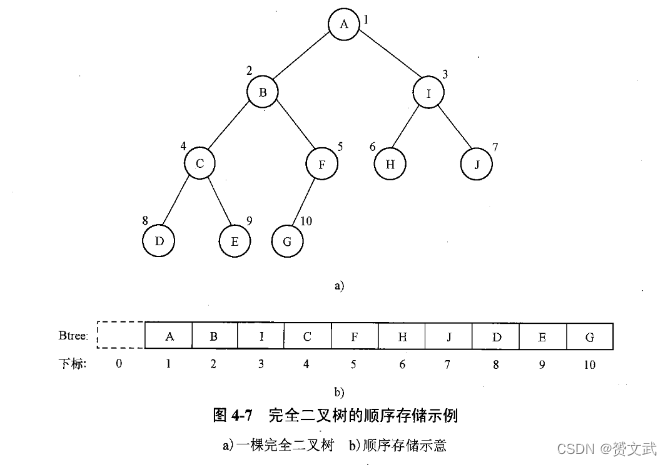
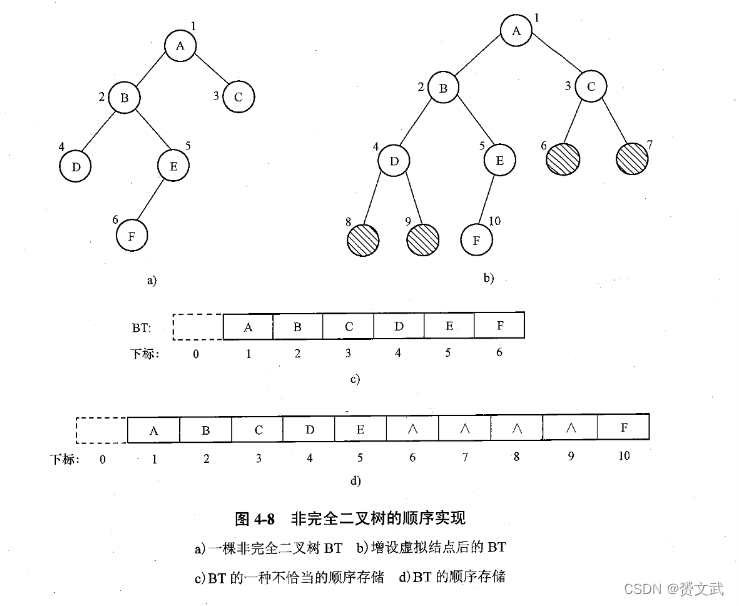
二叉树的链式存储结构

• 二叉树有不同的链式存储结构，最常用的是二叉链表与三叉链表

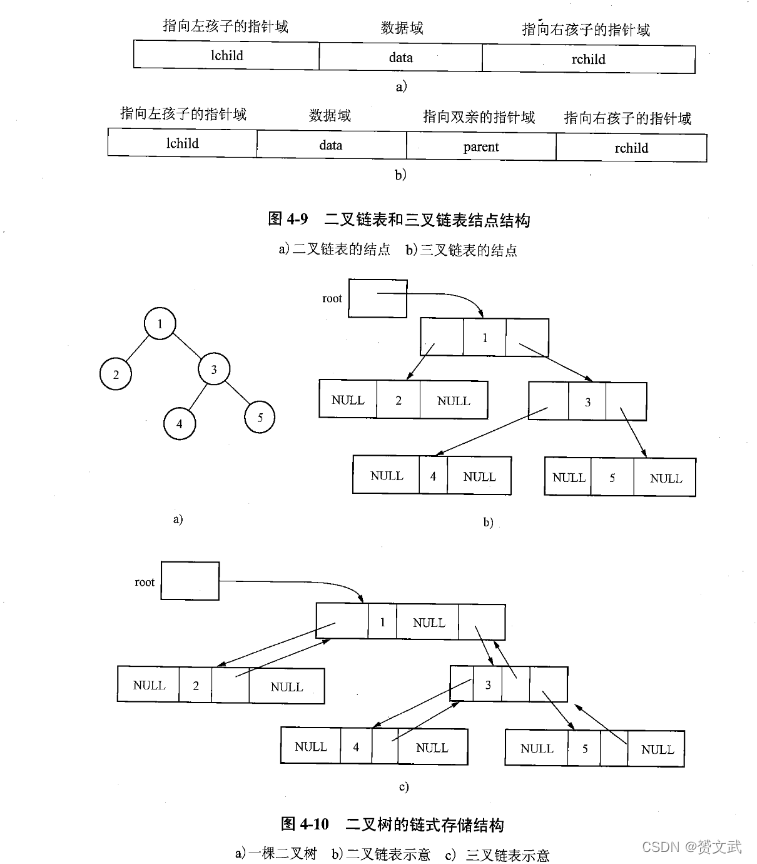
二叉树的遍历

二叉树遍历的递归实现

• 先序遍历
  • 访问根结点
  • 先序遍历左子树
  • 先序遍历右子树
• 中序遍历
  • 中序遍历左子树
  • 访问根结点
  • 中序遍历右子树
• 后序遍历
  • 后序遍历左子树
  • 后序遍历右子树
  • 访问根结点

二叉树的层次遍历

• 所谓二叉树层次遍历，是指从树的根结点开始逐层向下从左到右逐个访问

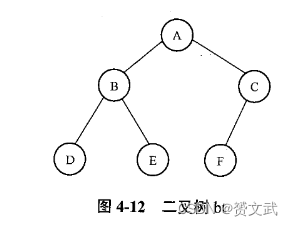
层次遍历的序列为ABCDEF

二叉树遍历的非递归实现

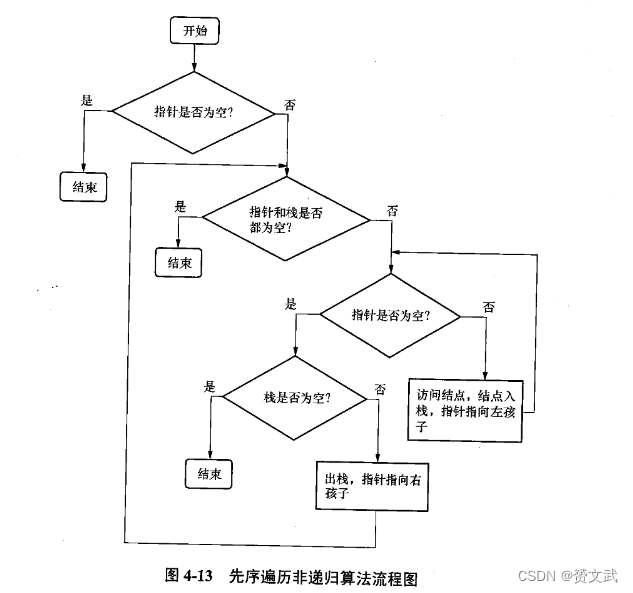
树和森林

树的存储结构

• 孩子链表表示法：一个数组元素个数和树中结点个数相同的一维数组

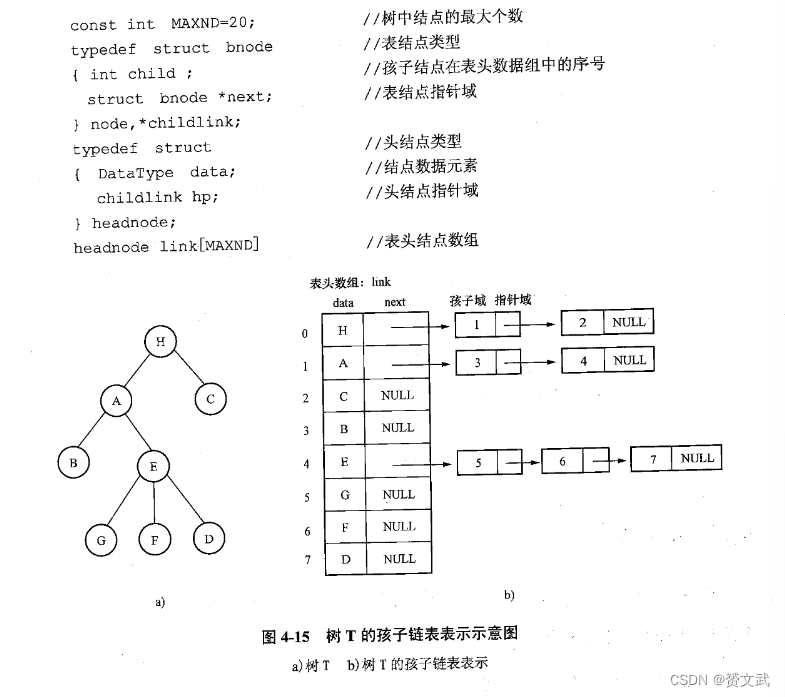
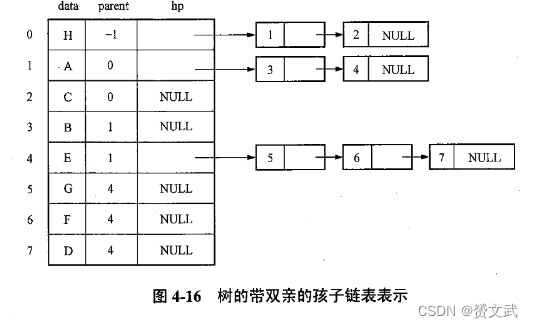
带双亲的孩子链表表示法如下：

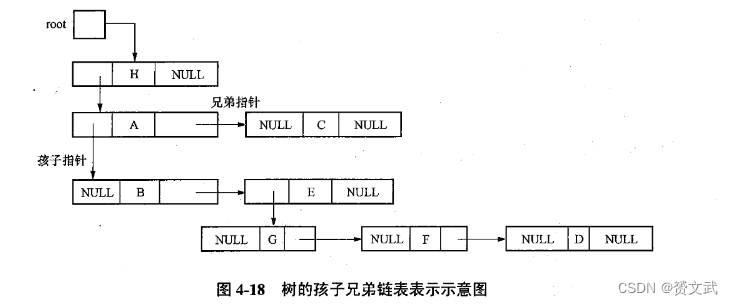
• 孩子兄弟链表表示法

• 双亲表示法（一维数组构成，每个分量包含数据域和双亲域）

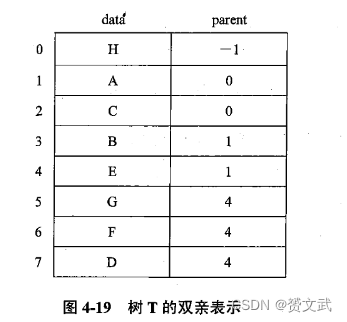
树、森林与二叉树的关系

• 树转换为二叉树
  • 将所有兄弟结点连接起来
  • 保留第一个兄弟结点与父结点的连接，断开其他兄弟结点与父结点的连接，然后以根结点为轴心按顺时针的方向旋转45度

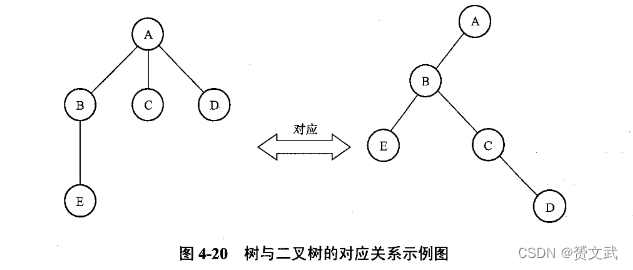
• 森林转换为二叉树
  • 将每棵树转换成相应的二叉树
  • 将前一步中得到的各颗二叉树的根结点看作是兄弟连接起来

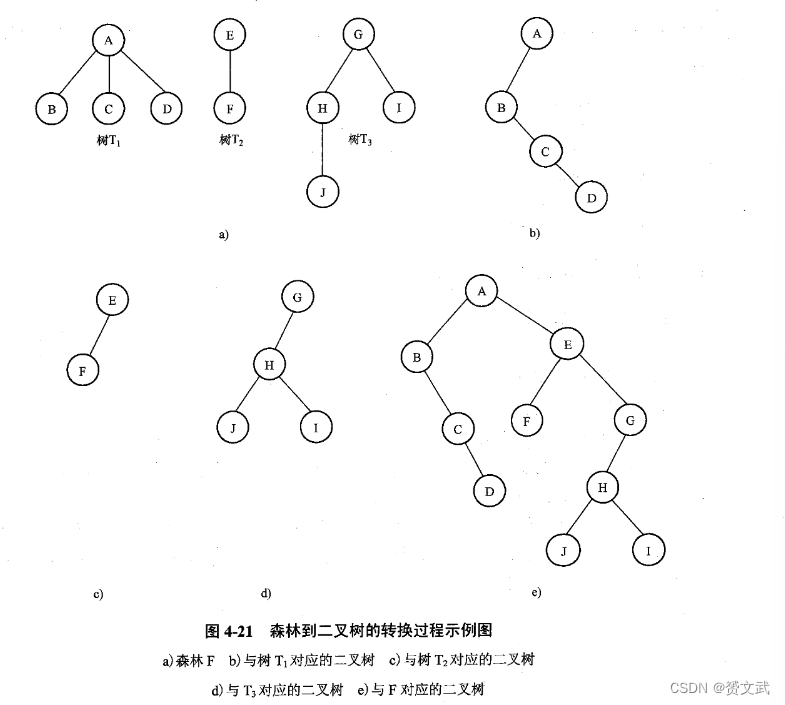
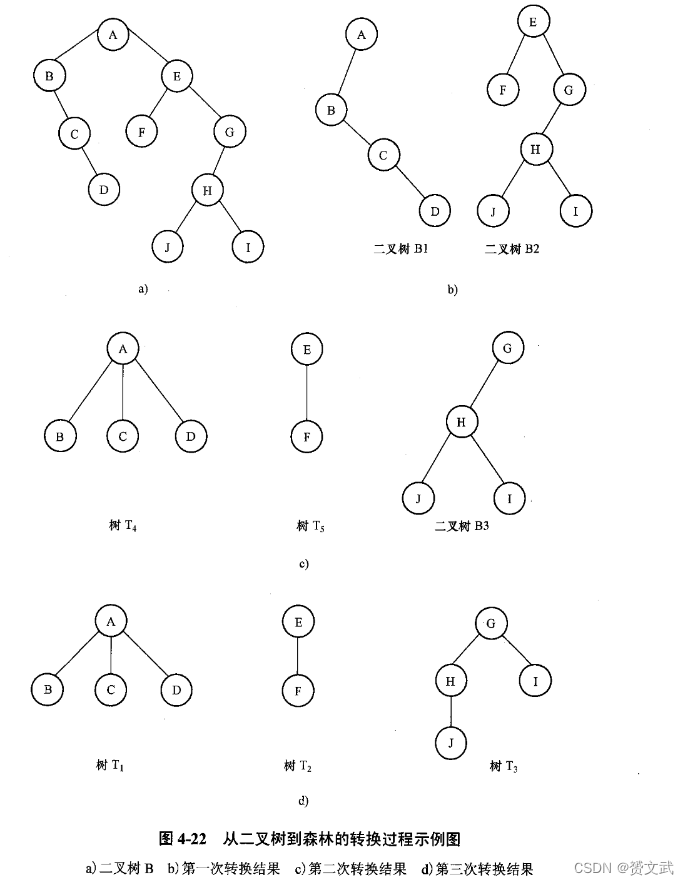
• 二叉树转为森林
  • 在待转换的二叉树中，断开根结点与右孩子的连线，得到两棵二叉树
  • 二叉树B1中A连接C、D，断开BC、BD的连线
  • 重复前两步

树和森林的遍历

• 树的遍历
  • 先序遍历：若树非空，访问根结点，依次先序遍历根的各棵子树
  • 后序遍历：依次后序遍历根的各棵子树，访问根结点
  • 层次遍历：若树非空，访问根结点；若i(i>=1)层结点已被访问，第i+1层结点尚未访问，则从左到右依次访问第i+1层结点
• 森林（非空）的遍历
  • 先序遍历森林；访问第一棵树的根结点；先序遍历第一棵树的根结点的子树组成的森林；先序遍历除去第一棵树之外其余树组成的森林
  • 中序遍历森林：中序遍历森林中第一棵树的根结点的子树组成的森林；访问第一棵树的根结点；中序遍历除去第一棵树之外其余树组成的森林

判定树和哈夫曼树

分类与判定树

• 分类是树的一种应用，其作用是将输入数据按预定的标准划分为不同的种类

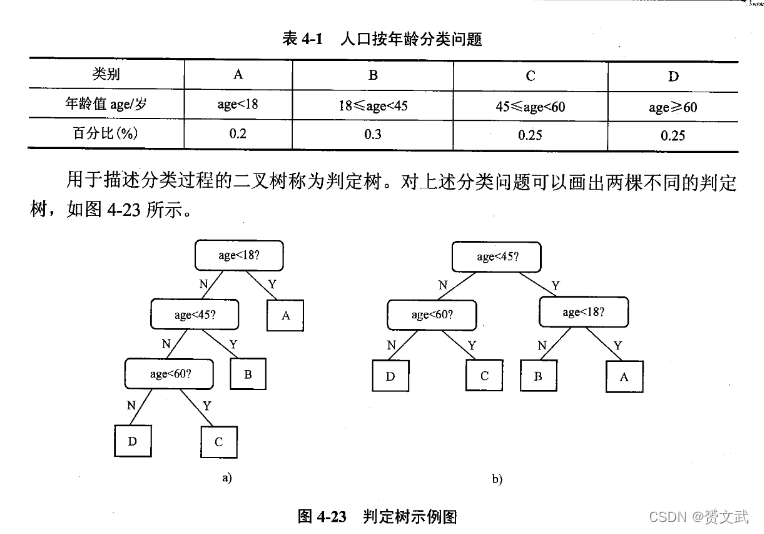
哈夫曼树和哈夫曼算法

哈夫曼树：当用 n 个结点（都做叶结点且都有各自的权值）试图构建一棵树时，如果构建的这棵树的带权路径长度（WPL）最小

• 权：树结点间的连线相关的数值（可以理解成线的长度，或者孩子的权重）叫做权
• 树的带权路径长度(WPL,Weighted Path Length)：树中所有叶结点的带权路径长度之和；WPL的值越小，说明构造出来的二叉树的性能就越优

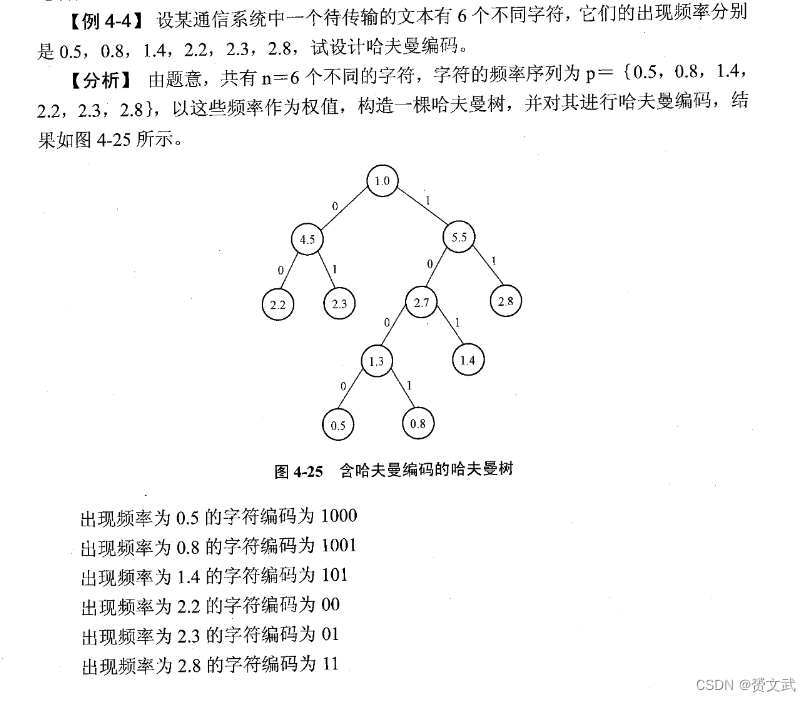
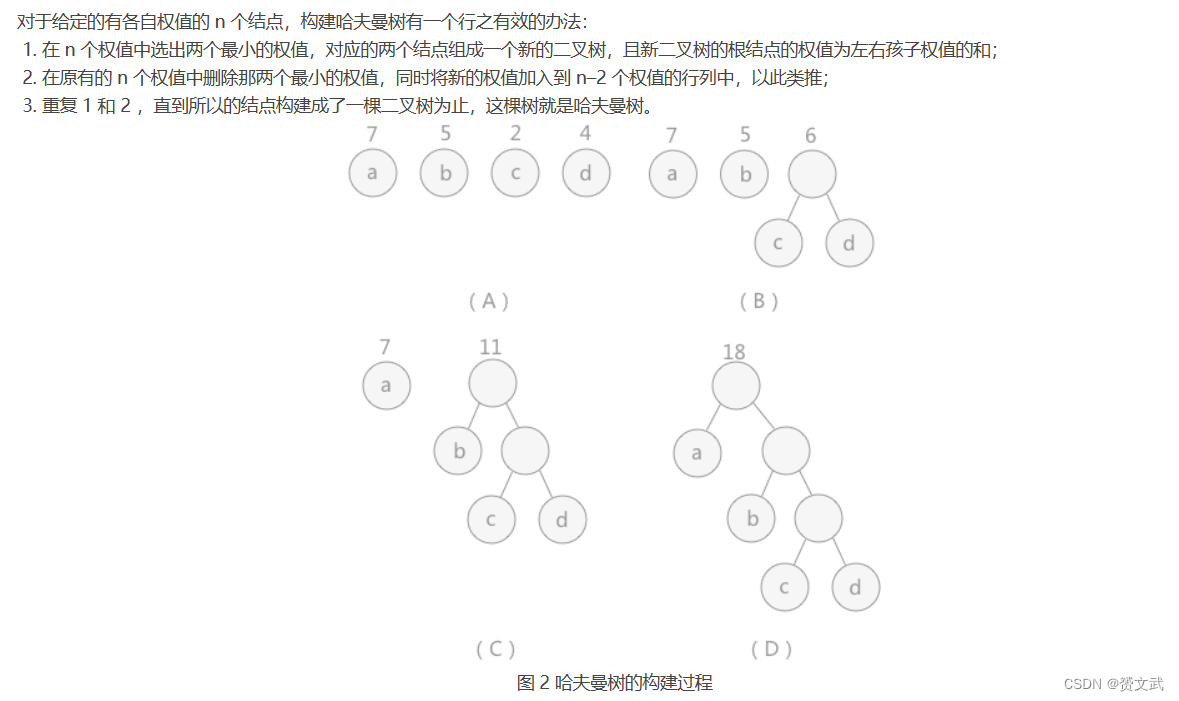
哈夫曼编码

牛刀小试

• 高度为K（K>=2）的完全二叉树至少有_____个叶子结点
• 一棵二叉树的先序序列和中序序列正好相反的充分必要条件是_______
• 深度为6（根层次为1）的二叉树至多有_______结点
• 已知二叉树的先序遍历序列为ABCFHIDGJE,中序遍历序列为AHIFCJGDEB，其后序遍历序列为_______
• 以数据集{4，7，9，11，16，23，30}为叶结点的权值，构建一棵哈夫曼树，并给出哈夫曼编码