大数据安全 | 【实验】DES加密解密

文章目录

📚DES介绍
📚基本流程
- 🐇初始IP置换和逆置换
- 🐇计算每一轮的子密钥
- 🐇迭代与F函数
- - ⭐️E扩展置换
  - ⭐️S盒压缩
  - ⭐️P盒置换
  - ⭐️最后的F函数及迭代实现
📚DES加密解密实现
📚关于雪崩效应

📚DES介绍

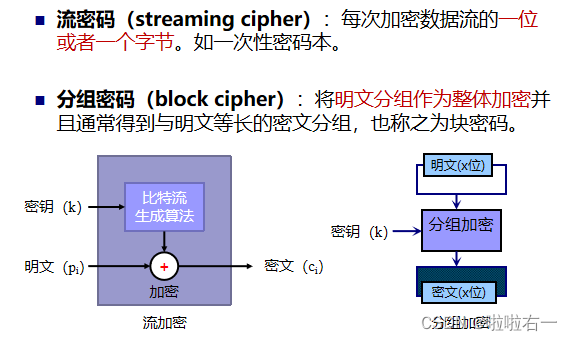
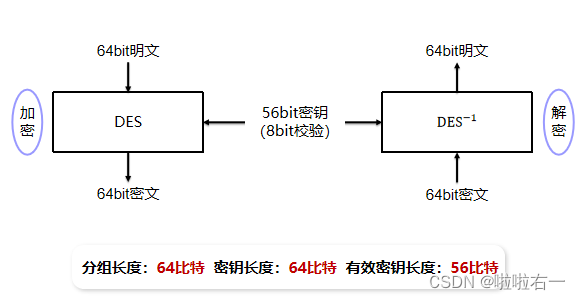
DES （Data Encryption Standard）是一种使用56位密钥对64位长分组进行加密的密码，是一种迭代算法。
DES算法是属于对称密码算法中的分组加密算法，是第一个公开的分组加密算法。
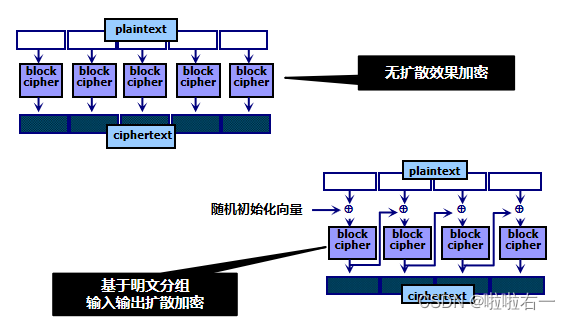
DES对明文中每个分组的加密过程都包含16轮，且每轮的操作都完全相同。每轮使用不同的子密钥，但是子密钥是从主密钥中推导而来。

📚基本流程

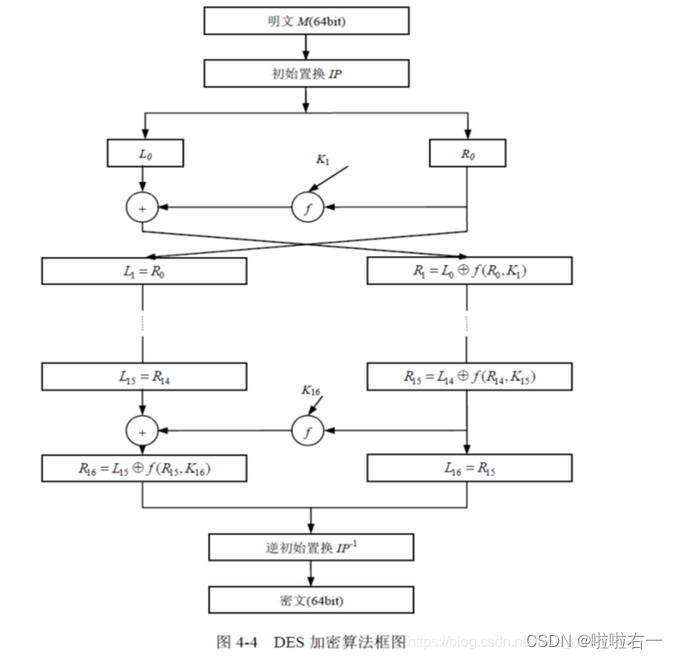
在这里插入图片描述

Step1：对明文二进制的一块（每64位为一块）进行IP置换
Step2：对IP置换后的数据进行切分，左32位 $L_0$ 、右32位 $R_0$
Step3：根据密钥计算每一轮的子密钥： $K_1$ 、 $K_2$ …、 $K_{16}$ （在这里我们从1开始标号，在后续代码中，考虑到索引从0开始，对应子密钥生成标号一并从0开始标）
Step4：获取得到下一轮的 $L_n$ 与 $R_n$ ，中间参与运算的有 $K_n$ ，以及F函数 等
Step5：重复步骤 4 操作16次
Step6：合并最后计算得到的 $L_{16}$ 与 $R_{16}$ 【注意看！这里最后R在左边L在右边】
Step7：进行IP逆置换得到最后的密文

🐇初始IP置换和逆置换

关于置换
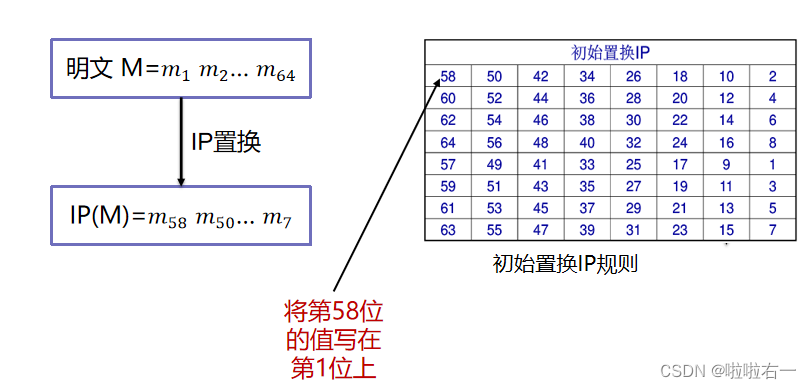
- 示例：明文的二进制为：
  0100100101001100010011110101011001000101010110010100111101010101
  （ILOVEYOU：每个字符以8位转换）
- 那么明文的第 1 为 0 需要置换为第 58 位的值，即 1，同理每一位按置换表重新排列。
- 故：IP置换后的数为：
  1111111110101000110111101111010100000000000000000110011101001100
- 同理IP逆置换也是一样的操作。
初始数据置换表IP
$\begin{bmatrix} 58&50&42&34&26&18&10&2&\\ 60&52&44&36&28&20&12&4&\\ 62&54&46&38&30&22&14&6&\\ 64&56&48&40&32&24&16&8&\\ 57&49&41&33&25&17&9&1&\\ 59&51&43&35&27&19&11&3&\\ 61&53&45&37&29&21&13&5&\\ 63&55&47&39&31&23&15&7 \end{bmatrix}$
最终置换表IP_1（逆置换表）
$\begin{bmatrix}40&8&48&16&56&24&64&32&\\ 39&7&47&15&55&23&63&31&\\ 38&6&46&14&54&22&62&30&\\ 37&5&45&13&53&21&61&29&\\ 36&4&44&12&52&20&60&28&\\ 35&3&43&11&51&19&59&27&\\ 34&2&42&10&50&18&58&26&\\ 33&1&41&9&49&17&57&25 \end{bmatrix}$
```
# 按照给定的置换表进行置换
def replace(self, table: str, replace_table: list) -> str:
     new_table = ""
     for i in replace_table:
         # 因为列表的索引是从0开始的，而替换表中的位置索引是从1开始的，所以需要进行减1的操作。
         new_table += table[i - 1]
     return new_table
```

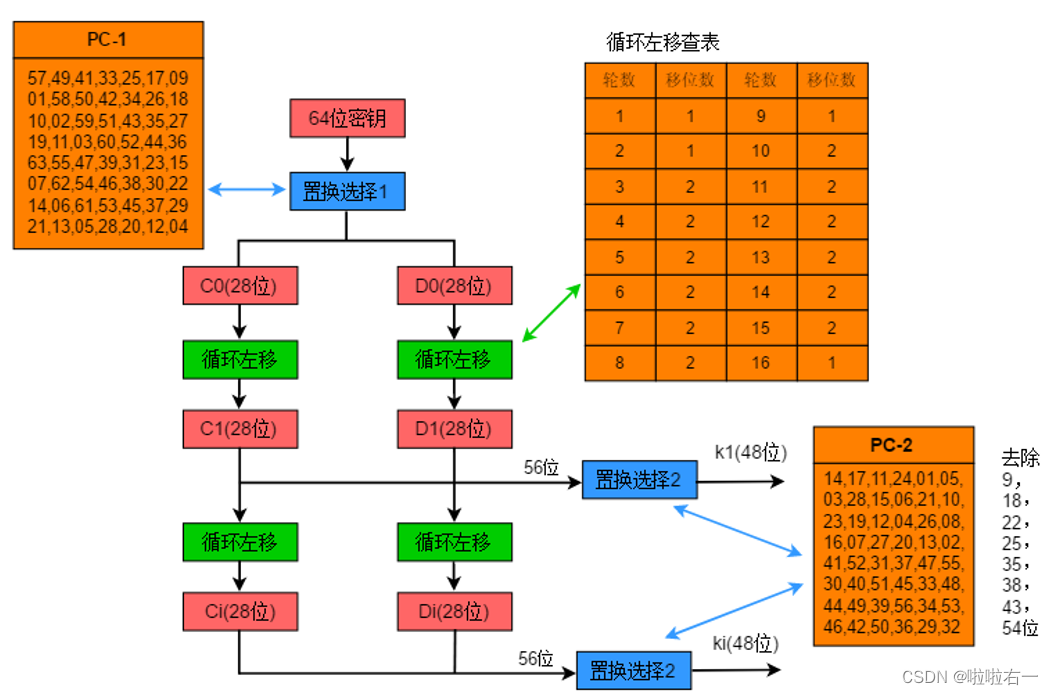
🐇计算每一轮的子密钥

DES的密钥每个字节的第8位作为奇偶校验位（8，16，24，32，40，48，56和64），密钥实际有效位为56位。
56位密钥由以下的密钥初始置换表（PC_1）置换默认密钥获得。
$\begin{bmatrix}57&49&41&33&25&17&9&\\ 1&58&50&42&34&26&18&\\ 10&2&59&51&43&35&27&\\ 19&11&3&60&52&44&36&\\ 63&55&47&39&31&23&15&\\ 7&62&54&46&38&30&22&\\ 14&6&61&53&45&37&29&\\ 21&13&5&28&20&12&4 \end{bmatrix}$
每一轮的子密钥由这56位密钥产生，生成方法如下：
- 将56位的密钥分成两部分，每部分28位
- 根据轮数，这两部分分别循环左移1位或两位（具体见下表）
  $\begin{bmatrix}1&1&2&2&2&2&2&2&1&2&2&2&2&2&2&1 \end{bmatrix}$
移动后，又从56位中选出48位（没有9,18,22,25,35,39,43,54）。通过置换，最终确定子密钥，这个过程称为密钥压缩置换。密钥压缩置换表PC_2如下：
$\begin{bmatrix}14&17&11&24&1&5&\\ 3&28&15&6&21&10&\\ 23&19&12&4&26&8&\\ 16&7&27&20&13&2&\\ 41&52&31&37&47&55&\\ 30&40&51&45&33&48&\\ 44&49&39&56&34&53&\\ 46&42&50&36&29&32 \end{bmatrix}$
```
 # 返回加密过程中16轮的子密钥
 def get_sonkey(self):
     # 56位密钥由密钥初始置换表（PC_1）置换默认密钥获得
     key = self.replace(self.K, self.PC_1)
     # 将56位的密钥分成两部分，每部分28位
     left_key = key[0:28]
     right_key = key[28:56]
     # 存储子密钥
     keys = []
     for i in range(0, 16):
         # 由轮换表确定当前轮次的移动次数
         move = self.k0[i]
         # 对左右部分分别进行移位操作
         move_left = left_key[move:28] + left_key[0:move]
         move_right = right_key[move:28] + right_key[0:move]
         # 更新left_key和right_key
         left_key = move_left
         right_key = move_right
         # 合并形成当前轮次的子密钥
         move_key = left_key + right_key
         # 按照密钥压缩置换表（PC_2）进行置换，得到长度为48位的子密钥ki，并将其添加到keys列表中。
         ki = self.replace(move_key, self.PC_2)
         keys.append(ki)
     # 返回加密过程中的16轮子密钥。
     return keys
```

在这里插入图片描述

解密时密钥的使用顺序与加密时的顺序应当相反。

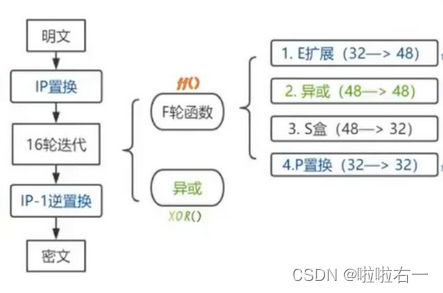
🐇迭代与F函数

由流程图可以得知 F 函数参数有 $R_n$ 以及 $K_n$ 。 $R_n$ 的长度是32位， $K_n$ 的长度是48（ $K_n$ 即为每一轮的子密钥）。
每一次迭代
- $L_n=R_{n-1}$
- $R_n=L_{n-1}\oplus {F(R_{n-1},K_n）}$
F函数
- E扩展置换：将右半部分数据 $R_n$ 从32位置换成48位，之后与当前子密钥进行异或运算
- S盒代替：将48位数据代替为32位数据。共有8个S盒，将E置换得到的48位数据，分为8组，每组6位，每个盒子输入6位输出4位，组合得到32位。
- P盒置换：S盒代替运算的32位输出按照P盒进行置换。该置换把输入的每位映射到输出位，任何一位不能被映射两次，也不能被略去，得到的数据还是32位的。

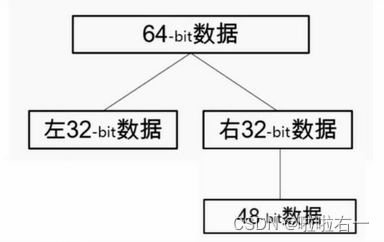
⭐️E扩展置换

将IP置换后获得的右半部分Rn，将32位输入扩展为48位(分为4位×8组)输出，生成与密钥相同长度的数据以进行异或运算。
E扩展表如下：
$\begin{bmatrix}32&1&2&3&4&5&\\ 4&5&6&7&8&9&\\ 8&9&10&11&12&13&\\ 12&13&14&15&16&17&\\ 16&17&18&19&20&21&\\ 20&21&22&23&24&25&\\ 24&25&26&27&28&29&\\ 28&29&30&31&32&1 \end{bmatrix}$
最外边两列是扩展的数据，分别是从相邻行上取/下取一位所得。表中第二行的4取自上组中的末位，9取自下组中的首位。

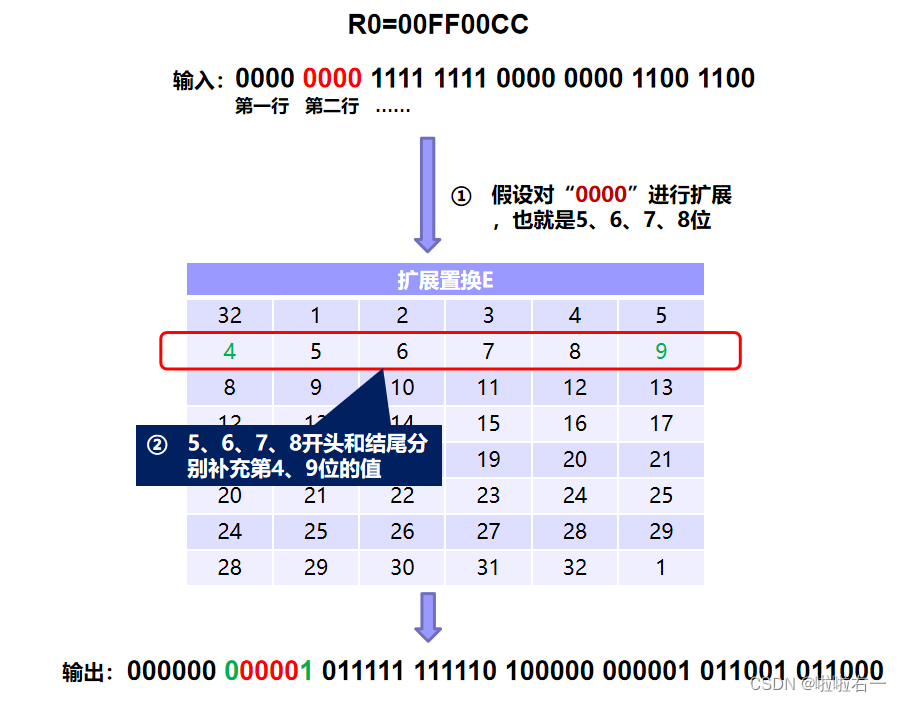
扩展置换之后，右半部分数据 $R_n$ 变为48位，与密钥置换得到的48位子密钥进行异或操作。

# 异或操作
def xor(self, xor1: str, xor2: str):
  size = len(xor1)
  result = ""
  for i in range(0, size):
      result += '0' if xor1[i] == xor2[i] else '1'
  return result

⭐️S盒压缩

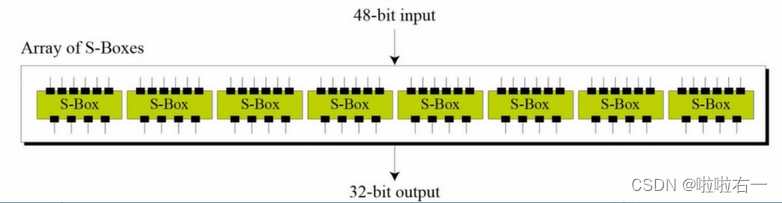
经过扩展的48位明文和48位密钥进行异或运算后，再使用8个S盒压缩处理得到32位数据
将48位分为8*6位
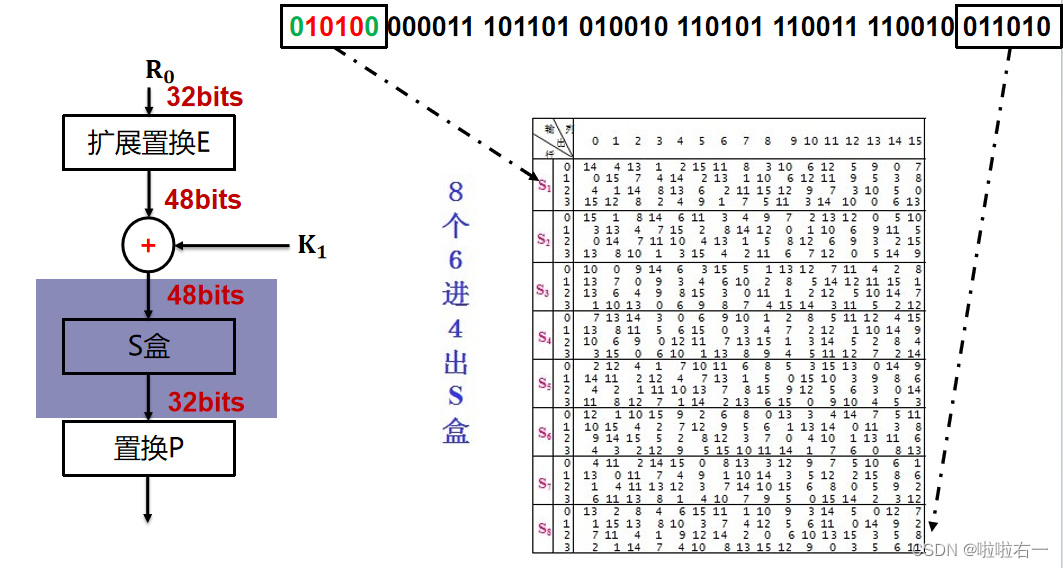
根据8个6进4出S盒进行压缩
每个S盒都是一个4行16列的表，盒中的每一项都是一个4位的数。
8*6位中第几个6位就对应第几个盒子。
6个输入确定了其对应的输出在哪一行哪一列，输入的首尾比特为行数H，中间四位比特为列数L，在S盒中查找第H行L列对应的数据。

代替过程产生8个4位的分组，在最后组合在一起形成32位数据。

# S盒代替
def s_box(self, xor_result: str):
    result = ""
    # 迭代8轮，每轮处理6位二进制数据
    for i in range(0, 8):
        # 将48位数据分为8组，每组6位，循环进行
        block = xor_result[i * 6:(i + 1) * 6]
        # 首尾比特得行数（十进制）
        line = int(block[0] + block[5], 2)
        # 中间四位比特得列数（十进制）
        column = int(block[1:4], 2)
        # 在S盒中查找，将所查到的十进制数转为二进制并通过[2:]切片去除二进制字符串的前缀"0b"
        res = bin(self.S[i][line * column])[2:]
        if len(res) < 4:
            # 如果结果的长度不足4位，则在左边用'0'进行填充
            res = '0' * (4 - len(res)) + res
        result += res
    # result中存储了经过S盒替换后的32位二进制数据
    return result

⭐️P盒置换

由S盒置换后得到的数据，进行P置换。P置换表如下：
$\begin{bmatrix}16&7&20&21&\\ 29&12&28&17&\\ 1&15&23&26&\\ 5&18&31&10&\\ 2&8&24&14&\\ 32&27&3&9&\\ 19&13&30&6&\\ 22&11&4&25 \end{bmatrix}$

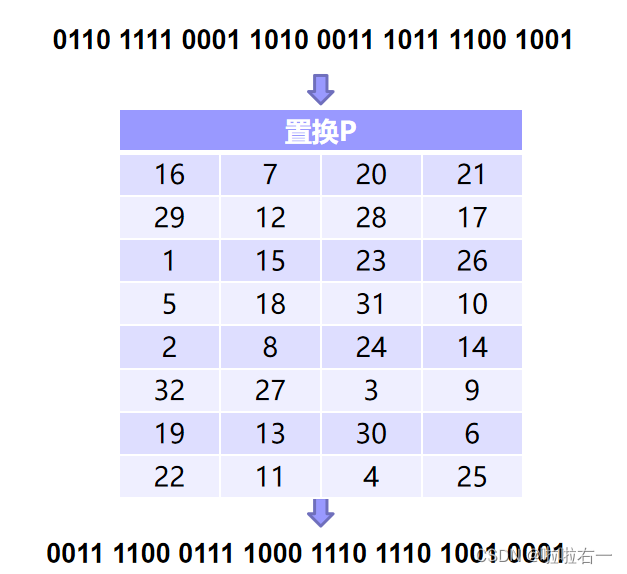
在这里插入图片描述

P盒置换之后就将结果与 $L_{n-1}$ 进行异或。

⭐️最后的F函数及迭代实现

F函数

# F函数，进行E扩展，与key异或操作，S盒替代及P盒置换操作后返回32位01字符串
def F_function(self, right: str, key: str):
    # 对right进行E扩展
    e_result = self.replace(right, self.E)
    # 与key 进行异或操作
    xor_result = self.xor(e_result, key)
    # 进入S盒子
    s_result = self.s_box(xor_result)
    # 进行P置换
    p_result = self.replace(s_result, self.P)
    return p_result

迭代实现

# 16轮迭代加密
def iteration(self, bin_plaintext: str, key_list: list):
  # 分组切分
  left = bin_plaintext[0:32]
  right = bin_plaintext[32:64]
  for i in range(0, 16):
      # L(n) = R(n-1)
      # R(n) = L(n-1)⊕F(R(n-1),K(n))
      next_left = right
      f_result = self.F_function(right, key_list[i])
      next_right = self.xor(left, f_result)
      left = next_left
      right = next_right
  # 注意看！这里最后R在左边，L在右边
  return right + left

📚DES加密解密实现

加密函数

# DES加密函数
def encrypt(self, plaintext):
  # 将给定明文转换为二进制
   plaintext_2 = self.convert_to_2(plaintext)
   # 将二进制明文分为64位一组的块
   plaintext_block = self.get_block(plaintext_2)
   # 存储加密后的分组
   ciphertext_block = []
   # 获取生成的16个子密钥列表
   key_list = self.get_sonkey()
   for block in plaintext_block:
       # 初代IP置换
       replaced_IP = self.replace(block, self.IP)
       # 16轮迭代操作
       ite_result = self.iteration(replaced_IP, key_list)
       # 逆IP置换
       replaced_IP_1 = self.replace(ite_result, self.IP_1)
       # 密文块replaced_IP_1添加到ciphertext_block列表中，以便后续拼接
       ciphertext_block.append(replaced_IP_1)
   ciphertext = ''.join(ciphertext_block)
   return ciphertext

解密函数

#DES解密函数
def decrypt(self, ciphertext):
 # 存储解密后的分组
  plaintext_block = []
  # 获取生成的16个子密钥列表
  key_list = self.get_sonkey()
  # 解密时密钥的使用顺序与加密时的顺序应当相反。
  key_list = key_list[::-1]
  # 将二进制密文分为64位一组的块
  ciphertext_block = [ciphertext[i:i + 64] for i in range(0, len(ciphertext), 64)]
  for block in ciphertext_block:
      # 初代IP置换
      replaced_IP = self.replace(block, self.IP)
      # 16轮迭代操作
      ite = self.iteration(replaced_IP, key_list)
      # 逆IP置换
      replaced_IP_1 = self.replace(ite, self.IP_1)
      # 明文块replaced_IP_1添加到plaintext_block列表中，以便后续拼接
      plaintext_block.append(replaced_IP_1)
  # 拼接，并移除其中的所有全零块。
  # 消除加密过程中可能引入的填充块，使得最终的二进制明文表示更加紧凑和直观。
  plaintext = ''.join(plaintext_block).replace('00000000', '')
  # 将二进制明文转为字符串返回
  return self.convert_to_str(plaintext)

完整代码

class DES():
    # 初始化DES加密的参数
    def __init__(self):
        # 初始数据置换表IP，用于初始IP置换
        self.IP = [
            58, 50, 42, 34, 26, 18, 10, 2,
            60, 52, 44, 36, 28, 20, 12, 4,
            62, 54, 46, 38, 30, 22, 14, 6,
            64, 56, 48, 40, 32, 24, 16, 8,
            57, 49, 41, 33, 25, 17, 9, 1,
            59, 51, 43, 35, 27, 19, 11, 3,
            61, 53, 45, 37, 29, 21, 13, 5,
            63, 55, 47, 39, 31, 23, 15, 7,
        ]
        # 密钥初始置换表PC_1，用于获得最初的56位密钥
        self.PC_1 = [
            57, 49, 41, 33, 25, 17, 9,
            1, 58, 50, 42, 34, 26, 18,
            10, 2, 59, 51, 43, 35, 27,
            19, 11, 3, 60, 52, 44, 36,
            63, 55, 47, 39, 31, 23, 15,
            7, 62, 54, 46, 38, 30, 22,
            14, 6, 61, 53, 45, 37, 29,
            21, 13, 5, 28, 20, 12, 4,
        ]
        # 密钥压缩置换表PC_2，用于获得子密钥
        self.PC_2 = [
            14, 17, 11, 24, 1, 5, 3, 28,
            15, 6, 21, 10, 23, 19, 12, 4,
            26, 8, 16, 7, 27, 20, 13, 2,
            41, 52, 31, 37, 47, 55, 30, 40,
            51, 45, 33, 48, 44, 49, 39, 56,
            34, 53, 46, 42, 50, 36, 29, 32,
        ]
        # 密钥每一轮的对应左移位数
        self.k0 = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1, ]
        # E扩展表，用于将右半部分数据Rn从32位置换成48位
        self.E = [
            32, 1, 2, 3, 4, 5,
            4, 5, 6, 7, 8, 9,
            8, 9, 10, 11, 12, 13,
            12, 13, 14, 15, 16, 17,
            16, 17, 18, 19, 20, 21,
            20, 21, 22, 23, 24, 25,
            24, 25, 26, 27, 28, 29,
            28, 29, 30, 31, 32, 1,
        ]
        # S盒，将48位数据代替为32位数据
        self.S = [
            [
                14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
                0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
                4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
                15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13,
            ],
            [
                15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
                3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
                0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
                13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9,
            ],
            [
                10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
                13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
                13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
                1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12,
            ],
            [
                7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
                13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
                10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
                3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14,
            ],
            [
                2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
                14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
                4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
                11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3,
            ],
            [
                12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
                10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
                9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
                4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13,
            ],
            [
                4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
                13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
                1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
                6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12,
            ],
            [
                13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
                1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
                7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
                2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11,
            ],
        ]
        # P盒置换表，S盒代替运算的32位输出按照P盒进行置换
        self.P = [
            16, 7, 20, 21,
            29, 12, 28, 17,
            1, 15, 23, 26,
            5, 18, 31, 10,
            2, 8, 24, 14,
            32, 27, 3, 9,
            19, 13, 30, 6,
            22, 11, 4, 25,
        ]
        # 最终置换表IP_1，用于逆置换
        self.IP_1 = [
            40, 8, 48, 16, 56, 24, 64, 32,
            39, 7, 47, 15, 55, 23, 63, 31,
            38, 6, 46, 14, 54, 22, 62, 30,
            37, 5, 45, 13, 53, 21, 61, 29,
            36, 4, 44, 12, 52, 20, 60, 28,
            35, 3, 43, 11, 51, 19, 59, 27,
            34, 2, 42, 10, 50, 18, 58, 26,
            33, 1, 41, 9, 49, 17, 57, 25,
        ]
        # 设置默认密钥
        self.K = '0110000101100010011000110110010001000001010000100100001101000100'

    # 进制转换——字符串转为二进制
    def convert_to_2(self, string: str) -> str:
        # 将字符串转成bytes类型，再转成list
        str_list = list(bytes(string, 'utf8'))
        result = []
        for num in str_list:
            # 用bin(num)将当前字节转换为二进制，然后使用[2:]切片操作去掉二进制字符串前面的"0b"标识。
            # 用zfill(8)函数给二进制字符串添加前导零，确保二进制字符串长度为8位
            # 一个字节由8个二进制位组成，保持一致性
            result.append(bin(num)[2:].zfill(8))
        # 将结果列表中的所有二进制字符串连接
        return "".join(result)

    # 进制转换——二进制转成字符串
    def convert_to_str(self, binary: str) -> str:
        # 将二进制字符串分组，每8位为一组
        bin_list = [binary[i:i + 8] for i in range(0, len(binary), 8)]
        # 存储每个8位二进制数字所代表的整数值
        list_int = []
        for b in bin_list:
            # 将当前8位二进制数转换为对应的十进制整数
            list_int.append(int(b, 2))
        # 将整数列表转换为字节序列,再解码得到字符串
        result = bytes(list_int).decode()
        return result

    # 对明文二进制进行分块，每64位为一块
    def get_block(self, binary: str) -> list:
        # 首先获取给定二进制字符串的长度
        len_binary = len(binary)
        if len_binary % 64 != 0:
            # 如果不能整除，说明按每64块分块不能刚好分块，需要添加前导零。
            new_binary = ("0" * (64 - (len_binary % 64))) + binary
            # 分块
            return [new_binary[i:i + 64] for i in range(0, len(new_binary), 64)]
        else:
            # 能被64整除，就不用补零，直接分块
            return [binary[j:j + 64] for j in range(0, len(binary), 64)]

    # 按照给定的置换表进行置换
    def replace(self, table: str, replace_table: list) -> str:
        new_table = ""
        for i in replace_table:
            # 因为列表的索引是从0开始的，而替换表中的位置索引是从1开始的，所以需要进行减1的操作。
            new_table += table[i - 1]
        return new_table

    # 返回加密过程中16轮的子密钥
    def get_sonkey(self):
        # 56位密钥由密钥初始置换表（PC_1）置换默认密钥获得
        key = self.replace(self.K, self.PC_1)
        # 将56位的密钥分成两部分，每部分28位
        left_key = key[0:28]
        right_key = key[28:56]
        # 存储子密钥
        keys = []
        for i in range(0, 16):
            # 由轮换表确定当前轮次的移动次数
            move = self.k0[i]
            # 对左右部分分别进行移位操作
            move_left = left_key[move:28] + left_key[0:move]
            move_right = right_key[move:28] + right_key[0:move]
            # 更新left_key和right_key
            left_key = move_left
            right_key = move_right
            # 合并形成当前轮次的子密钥
            move_key = left_key + right_key
            # 按照密钥压缩置换表（PC_2）进行置换，得到长度为48位的子密钥ki，并将其添加到keys列表中。
            ki = self.replace(move_key, self.PC_2)
            keys.append(ki)
        # 返回加密过程中的16轮子密钥。
        return keys

    # 异或操作
    def xor(self, xor1: str, xor2: str):
        size = len(xor1)
        result = ""
        for i in range(0, size):
            result += '0' if xor1[i] == xor2[i] else '1'
        return result

    # S盒代替
    def s_box(self, xor_result: str):
        result = ""
        # 迭代8轮，每轮处理6位二进制数据
        for i in range(0, 8):
            # 将48位数据分为8组，循环进行
            block = xor_result[i * 6:(i + 1) * 6]
            # 首尾比特得行数
            line = int(block[0] + block[5], 2)
            # 中间四位比特得列数
            column = int(block[1:4], 2)
            # 在S盒中查找，将所得转为二进制并通过[2:]切片去除二进制字符串的前缀"0b"
            res = bin(self.S[i][line * column])[2:]
            if len(res) < 4:
                # 如果结果的长度不足4位，则在左边用'0'进行填充
                res = '0' * (4 - len(res)) + res
            result += res
        # result中存储了经过S盒替换后的32位二进制数据
        return result

    # F函数，进行E扩展，与key异或操作，S盒替代及P盒置换操作后返回32位01字符串
    def F_function(self, right: str, key: str):
        # 对right进行E扩展
        e_result = self.replace(right, self.E)
        # 与key 进行异或操作
        xor_result = self.xor(e_result, key)
        # 进入S盒子
        s_result = self.s_box(xor_result)
        # 进行P置换
        p_result = self.replace(s_result, self.P)
        return p_result

    # 16轮迭代加密
    def iteration(self, bin_plaintext: str, key_list: list):
        # 分组切分
        left = bin_plaintext[0:32]
        right = bin_plaintext[32:64]
        for i in range(0, 16):
            # L(n) = R(n-1)
            # R(n) = L(n-1)⊕F(R(n-1),K(n))
            next_left = right
            f_result = self.F_function(right, key_list[i])
            next_right = self.xor(left, f_result)
            left = next_left
            right = next_right
        # 最后R在左边,L在右边
        return right + left

    # DES加密函数
    def encrypt(self, plaintext):
        # 将给定明文转换为二进制
        plaintext_2 = self.convert_to_2(plaintext)
        # 将二进制明文分为64位一组的块
        plaintext_block = self.get_block(plaintext_2)
        # 存储加密后的分组
        ciphertext_block = []
        # 获取生成的16个子密钥列表
        key_list = self.get_sonkey()
        for block in plaintext_block:
            # 初代IP置换
            replaced_IP = self.replace(block, self.IP)
            # 16轮迭代操作
            ite_result = self.iteration(replaced_IP, key_list)
            # 逆IP置换
            replaced_IP_1 = self.replace(ite_result, self.IP_1)
            # 密文块replaced_IP_1添加到ciphertext_block列表中，以便后续拼接
            ciphertext_block.append(replaced_IP_1)
        ciphertext = ''.join(ciphertext_block)
        return ciphertext

    #DES解密函数
    def decrypt(self, ciphertext):
        # 存储解密后的分组
        plaintext_block = []
        # 获取生成的16个子密钥列表
        key_list = self.get_sonkey()
        # 解密时密钥的使用顺序与加密时的顺序应当相反。
        key_list = key_list[::-1]
        # 将二进制密文分为64位一组的块
        ciphertext_block = [ciphertext[i:i + 64] for i in range(0, len(ciphertext), 64)]
        for block in ciphertext_block:
            # 初代IP置换
            replaced_IP = self.replace(block, self.IP)
            # 16轮迭代操作
            ite = self.iteration(replaced_IP, key_list)
            # 逆IP置换
            replaced_IP_1 = self.replace(ite, self.IP_1)
            # 明文块replaced_IP_1添加到plaintext_block列表中，以便后续拼接
            plaintext_block.append(replaced_IP_1)
        # 拼接，并移除其中的所有全零块。
        # 消除加密过程中可能引入的填充块，使得最终的二进制明文表示更加紧凑和直观。
        plaintext = ''.join(plaintext_block).replace('00000000', '')
        # 将二进制明文转为字符串返回
        return self.convert_to_str(plaintext)

    def main(self):
        select = input("加密（1） or 解密（2）\n")
        if select == '1':
            plaintext = input("输入要加密的明文：")
            ciphertext = self.encrypt(plaintext)
            print("加密得:{}".format(ciphertext))
        elif select == '2':
            plaintext = input("输入要解密的密文：")
            plaintext = self.decrypt(plaintext)
            print("解密得:{}".format(plaintext))
        else:
            input("重新选择！")
            self.main()


if __name__ == '__main__':
    DES = DES()
    while True:
        DES.main()
        print("")

在这里插入图片描述 100001010011101100000001000001100010100000101110000010001011100001010101000101100100000001110110001000000100001000111101101110010011101000000110101110010000100000110100101001011000010101100000

📚关于雪崩效应

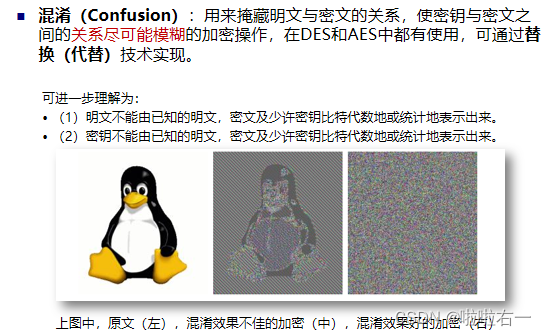
雪崩效应是指：明文或秘钥的某一位发生变化会导致密文的很多位发生改变。
这意味着对于输入数据的任何微小更改，加密结果都应该是随机且不可预测的，这是密码学安全的重要特性之一。

已知密钥abcdABCD
明文块1为（0000000000000000000000000000000000000000000000000000000000000000）
明文块2为（1000000000000000000000000000000000000000000000000000000000000000）
使用同一密钥对两组明文分别进行加密，统计两个密文块间不同数据位的数量

所得的密文分别是：

00111001111011111101000110110111010111000101001000110110111010110011100111101111110100011011011101011100010100100011011011101011001110011110111111010001101101110101110001010010001101101110101100111001111011111101000110110111010111000101001000110110111010110011100111101111110100011011011101011100010100100011011011101011001110011110111111010001101101110101110001010010001101101110101100111001111011111101000110110111010111000101001000110110111010110011100111101111110100011011011101011100010100100011011011101011
10011001010101001001000000001100100011100101100011011000001100010011100111101111110100011011011101011100010100100011011011101011001110011110111111010001101101110101110001010010001101101110101100111001111011111101000110110111010111000101001000110110111010110011100111101111110100011011011101011100010100100011011011101011001110011110111111010001101101110101110001010010001101101110101100111001111011111101000110110111010111000101001000110110111010110011100111101111110100011011011101011100010100100011011011101011

def count_different_bits(bin_str1, bin_str2):
    # 检查两个二进制字符串长度是否相同
    if len(bin_str1) != len(bin_str2):
        return -1  # 返回-1代表长度不匹配
    # 统计不同位的数量
    count = 0
    for i in range(len(bin_str1)):
        if bin_str1[i] != bin_str2[i]:
            count += 1
    return count

bin_str1 = "00111001111011111101000110110111010111000101001000110110111010110011100111101111110100011011011101011100010100100011011011101011001110011110111111010001101101110101110001010010001101101110101100111001111011111101000110110111010111000101001000110110111010110011100111101111110100011011011101011100010100100011011011101011001110011110111111010001101101110101110001010010001101101110101100111001111011111101000110110111010111000101001000110110111010110011100111101111110100011011011101011100010100100011011011101011"
bin_str2 = "10011001010101001001000000001100100011100101100011011000001100010011100111101111110100011011011101011100010100100011011011101011001110011110111111010001101101110101110001010010001101101110101100111001111011111101000110110111010111000101001000110110111010110011100111101111110100011011011101011100010100100011011011101011001110011110111111010001101101110101110001010010001101101110101100111001111011111101000110110111010111000101001000110110111010110011100111101111110100011011011101011100010100100011011011101011"

result = count_different_bits(bin_str1, bin_str2)
print("这两个二进制序列有", result, "位不同。")