什么是递归：递归的思想是把一个大型复杂问题层层转化为一个与原问题规模更小的问题，问题被拆解成子问题后，递归调用继续进行，直到子问题无需进一步递归就可以解决的地步为止。

说白话就是函数自己调自己。

再翻译白话：

1.大问题可以拆分为若干小问题
2.原问题与子问题除数据规模不同，求解思路完全相同
3.存在递归终止条件

第一个例子从1到n累加（实操）

说明：本机配置

function mysum(n) {
  if (n == 1) {
    return 1
  }
  return mysum(n - 1) + n
}

function mysum01(n) {
  return (n * (n + 1)) / 2
}

var beginTime = new Date()
console.log(mysum(10000))
var endTime = new Date()
console.log('递归用时：' + (endTime - beginTime) + 'ms')

beginTime = new Date()
console.log(mysum01(1e+154))
endTime = new Date()
console.log('用时：' + (endTime - beginTime) + 'ms')

运行结果：

50005000
递归用时：2ms
5e+307
用时：0ms

说明：递归算法，100000时内存溢出，第二中算法最大试验值为1e+154.均为新自动手测试。

递归的运算过程

第二个例子：阶乘

function Factorial(n) {
  return n==0 ? 1 : n * Factorial(n-1);
}

var beginTime = new Date()
console.log(Factorial(170))
var endTime = new Date()
console.log('递归用时：' + (endTime - beginTime) + 'ms')

运行结果：

7.257415615307994e+306
递归用时：2ms

说明本机测试N的最大值为 170.

第三个例子： 斐波那契数列

斐波那契数列的排列是：1，1，2，3，5，8，13，21，34，55，89，144……依次类推下去，你会发现，它后一个数等于前面两个数的和。在这个数列中的数字，就被称为斐波那契数
首先分析思路：一个数等于前两个数之和
然后分析表达式：

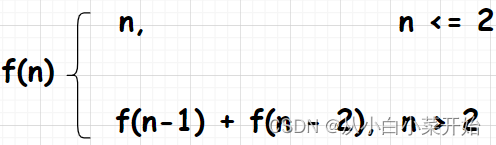
function Fib(n) {
  if (n <= 2) return 1
  //n > 2时继续调用Fib函数
  else return Fib(n - 1) + Fib(n - 2)
}

var beginTime = new Date()
console.log(Fib(45))
var endTime = new Date()
console.log('递归用时：' + (endTime - beginTime) + 'ms')

运行结果：

1134903170
递归用时：4712ms

本机测试最大n值为 45.

总结：

优点

1.简洁性：递归可以用较少的代码实现复杂的功能。相对于使用循环来处理嵌套结构，递归代码通常更简洁、易于理解和维护。

2.可读性：递归可以使代码更加可读和自解释。它可以更直观地表示问题的解决方案，特别是对于涉及嵌套结构的问题。

3.灵活性：递归可以应对未知深度的数据结构，因为它不需要提前知道要处理的嵌套层级。

4.问题分解：递归通过将问题划分为更小的子问题，使得复杂问题的解决变得更加可行。

缺点

1.性能开销：递归可能会导致性能问题，尤其是当递归层级很深时。每次递归调用都需要在内存中创建一个新的函数上下文，这可能会占用大量的内存和处理时间。

2.栈溢出：如果递归层级过深，函数调用的堆栈可能会超出系统的限制，导致栈溢出错误。这通常可以通过限制递归层级或使用尾递归优化来避免。

3.难以调试：由于递归涉及到函数的自我调用，调试递归函数可能会变得复杂和困难。错误的递归调用可能导致死循环或无限递归，从而使得调试变得更加困难。