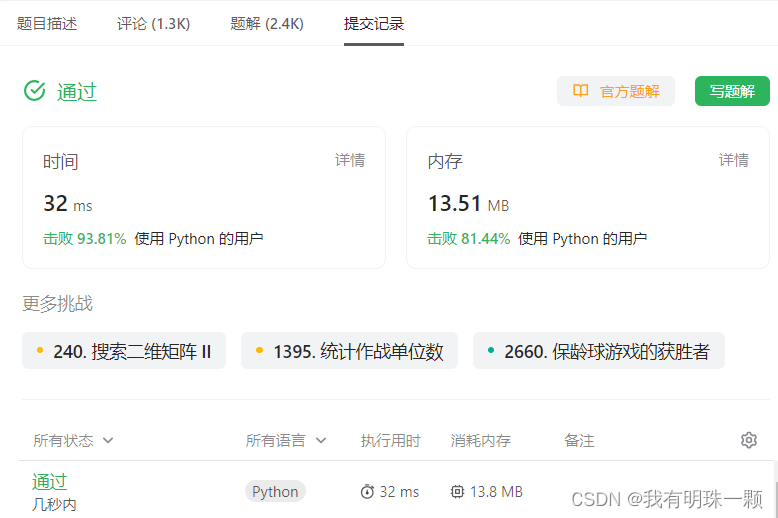
122. 买卖股票的最佳时机 II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。
在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。
返回 你能获得的 最大 利润 。

问题转换 + 贪心

只要明天比今天价格高就在今天买入明天卖出，吃掉所有收益一定能达成题意要求的收益

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        res = 0
        if len(prices) == 1:
            return res
        for i in range(1, len(prices)):
            tmp = prices[i] - prices[i - 1]
            res += (tmp if tmp > 0 else 0)
        return res

动态规划

下面网友写的题解十分精彩，从状态转移方程可以看出计算i只需i-1，可以进行滚动优化

作者：liweiwei1419
链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/solutions/38498/tan-xin-suan-fa-by-liweiwei1419-2/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

第 1 步：定义状态

状态 dp[i][j] 定义如下：

dp[i][j] 表示到下标为 i 的这一天，持股状态为 j 时，我们手上拥有的最大现金数。

注意：限定持股状态为 j 是为了方便推导状态转移方程，这样的做法满足 无后效性。

其中：

第一维 i 表示下标为 i 的那一天（ 具有前缀性质，即考虑了之前天数的交易 ）；
第二维 j 表示下标为 i 的那一天是持有股票，还是持有现金。这里 0 表示持有现金（cash），1 表示持有股票（stock）。

第 2 步：思考状态转移方程

状态从持有现金（cash）开始，到最后一天我们关心的状态依然是持有现金（cash）；
每一天状态可以转移，也可以不动。状态转移用下图表示：

（状态转移方程写在代码中）

说明：

由于不限制交易次数，除了最后一天，每一天的状态可能不变化，也可能转移；
写代码的时候，可以不用对最后一天单独处理，输出最后一天，状态为 0 的时候的值即可。

第 3 步：确定初始值

起始的时候：

如果什么都不做，dp[0][0] = 0；
如果持有股票，当前拥有的现金数是当天股价的相反数，即 dp[0][1] = -prices[i]；

第 4 步：确定输出值

终止的时候，上面也分析了，输出 dp[len - 1][0]，因为一定有 dp[len - 1][0] > dp[len - 1][1]。

public class Solution {

    public int maxProfit(int[] prices) {
        int len = prices.length;
        if (len < 2) {
            return 0;
        }

        // 0：持有现金
        // 1：持有股票
        // 状态转移：0 → 1 → 0 → 1 → 0 → 1 → 0
        int[][] dp = new int[len][2];

        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        for (int i = 1; i < len; i++) {
            // 这两行调换顺序也是可以的
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }
        return dp[len - 1][0];
    }
}

复杂度分析：

时间复杂度：O(N)，这里 N 表示股价数组的长度；
空间复杂度：O(N)，虽然是二维数组，但是第二维是常数，与问题规模无关。