XGBoost 2.0:对基于树的方法进行了重大更新

XGBoost是处理不同类型表格数据的最著名的算法，LightGBM 和Catboost也是为了修改他的缺陷而发布的。9月12日XGBoost发布了新的2.0版，本文除了介绍让XGBoost的完整历史以外，还将介绍新机制和更新。

这是一篇很长的文章，因为我们首先从梯度增强决策树开始。

基于树的方法，如决策树、随机森林以及扩展后的XGBoost，在处理表格数据方面表现出色，这是因为它们的层次结构天生就善于对表格格式中常见的分层关系进行建模。它们在自动检测和整合特征之间复杂的非线性相互作用方面特别有效。另外这些算法对输入特征的规模具有健壮性，使它们能够在不需要规范化的情况下在原始数据集上表现良好。

最终要的一点是它们提供了原生处理分类变量的优势，绕过了对one-hot编码等预处理技术的需要，尽管XGBoost通常还是需要数字编码。

另外还有一点是基于树的模型可以轻松地可视化和解释，这进一步增加了吸引力，特别是在理解表格数据结构时。通过利用这些固有的优势，基于树的方法——尤其是像XGBoost这样的高级方法——非常适合处理数据科学中的各种挑战，特别是在处理表格数据时。

决策树

在更严格的数学语言中，决策树表示一个函数T:X→Y，其中X是特征空间，Y可以是连续值(在回归的情况下)或类标签(在分类的情况下)。我们可以将数据分布表示为D和真函数f:X→Y。决策树的目标是找到与f(x)非常接近的T(x)，理想情况下是在概率分布D上。

损失函数

与树T相关的风险R相对于f表示为T(x)和f(x)之间的损失函数的期望值:

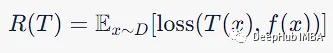
构建决策树的主要目标是构建一个能够很好地泛化到新的、看不见的数据的模型。在理想情况下，我们知道数据的真实分布D，可以直接计算任何候选决策树的风险或预期损失。但是在实践中真实的分布是未知的。

所以我们依赖于可用数据的子集来做出决策。这就是启发式方法的概念出现的地方。

基尼系数

基尼指数是一种杂质度量，用于量化给定节点中类别的混合程度。给定节点t的基尼指数G的公式为:

式中p_i为节点t中属于第i类样本的比例，c为类的个数。

基尼指数的范围从0到0.5，其中较低的值意味着节点更纯粹(即主要包含来自一个类别的样本)。

基尼指数还是信息增益?

基尼指数(Gini Index)和信息增益(Information Gain)都是量化区分不同阶层的特征的“有用性”的指标。从本质上讲，它们提供了一种评估功能将数据划分为类的效果的方法。通过选择杂质减少最多的特征(最低的基尼指数或最高的信息增益)，就可以做出一个启发式决策，这是树生长这一步的最佳局部选择。

过拟合和修剪

决策树也会过度拟合，尤其是当它们很深的时候，会捕获数据中的噪声。有两个主要策略可以解决这个问题:

分割:随着树的增长，持续监控它在验证数据集上的性能。如果性能开始下降，这是停止生长树的信号。
后修剪:在树完全生长后，修剪不能提供太多预测能力的节点。这通常是通过删除节点并检查它是否会降低验证准确性来完成的。如果不是则修剪节点。

找不到最优风险最小化的树，是因为我们不知道真实的数据分布d。所以只能使用启发式方法，如基尼指数或信息增益，根据可用数据局部优化树，而谨慎分割和修剪等技术有助于管理模型的复杂性，避免过拟合。

随机森林

随机森林是决策树T_1, T_2， …的集合， T_n，其中每个决策树T_i:X→Y将输入特征空间X映射到输出Y，输出Y可以是连续值(回归)或类标签(分类)。

随机森林集合定义了一个新函数R:X→Y，它对所有单个树的输出进行多数投票(分类)或平均(回归)，数学上表示为:

与决策树一样，随机森林也旨在近似概率分布D上的真实函数f:X→Y。D在实践中通常是未知的，因此有必要使用启发式方法来构建单个树。

与随机森林相关的相对于f的风险R_RF是R(x)和f(x)之间损失函数的期望值。考虑到R是T的集合，风险通常低于与单个树相关的风险，这有助于泛化:

过拟合和Bagging

与单一决策树相比，随机森林不太容易过度拟合，这要归功于Bagging和特征随机化，这在树之间创造了多样性。风险在多棵树上平均，使模型对数据中的噪声更有弹性。

随机森林中的Bagging实现了多个目标:它通过在不同的树上平均预测来减少过拟合，每棵树都在不同的自举样本上训练，从而使模型对数据中的噪声和波动更具弹性。这也减少了方差可以得到更稳定和准确的预测。树的集合可以捕获数据的不同方面，提高了模型对未见数据的泛化。并且还可以提供更高的健壮性，因为来自其他树的正确预测通常会抵消来自单个树的错误。该技术可以增强不平衡数据集中少数类的表示，使集成更适合此类挑战。

随机森林它在单个树级别采用启发式方法，但通过集成学习减轻了一些限制，从而在拟合和泛化之间提供了平衡。Bagging和特征随机化等技术进一步降低了风险，提高了模型的健壮性。

梯度增强决策树

梯度增强决策树(GBDT)也是一种集成方法，它通过迭代地增加决策树来构建一个强预测模型，每棵新树旨在纠正现有集成的错误。在数学上，GBDT也表示一个函数T:X→Y，但它不是找到一个单一的T(X)，而是形成一个弱学习器t_1(X)， t_2(X)，…的序列，它们共同工作以近似真实函数f(X)。与随机森林(Random Forest)通过Bagging独立构建树不同，GBDT在序列中构建树，使用梯度下降最小化预测值和真实值之间的差异，通常通过损失函数表示。

在GBDT中，在构建每棵树并进行预测之后，计算预测值与实际值之间的残差(或误差)。这些残差本质上是梯度的一种形式——表明损失函数是如何随其参数变化的。然后一个新的树适合这些残差，而不是原始的结果变量，有效地采取“步骤”，利用梯度信息最小化损失函数。这个过程是重复的，迭代地改进模型。

“梯度”一词意味着使用梯度下降优化来指导树的顺序构建，旨在不断最小化损失函数，从而使模型更具预测性。

为什么它比决策树和随机森林更好?

减少过拟合:与随机森林一样，GBDT也避免过拟合，但它是通过构建浅树(弱学习器)和优化损失函数来实现的，而不是通过平均或投票。
高效率:GBDT专注于难以分类的实例，更多地适应数据集的问题区域。这可以使它在分类性能方面比随机森林更有效，因为随机森林对所有实例都一视同仁。
优化损失函数:与启发式方法(如基尼指数或信息增益)不同，GBDT中的损失函数在训练期间进行了优化，允许更精确地拟合数据。
更好的性能:当选择正确的超参数时，GBDT通常优于随机森林，特别是在需要非常精确的模型并且计算成本不是主要关注点的情况下。
灵活性:GBDT既可以用于分类任务，也可以用于回归任务，而且它更容易优化，因为您可以直接最小化损失函数。

梯度增强决策树解决的问题

单个树的高偏差:GBDT通过迭代修正单个树的误差，可以获得比单个树更高的性能。

模型复杂性:随机森林旨在减少模型方差，而GBDT在偏差和方差之间提供了一个很好的平衡，通常可以获得更好的整体性能。

梯度增强决策树比决策树和随机森林具有性能、适应性和优化方面的优势。当需要较高的预测准确性并愿意花费计算资源来微调模型时，它们特别有用。

XGBoost

在关于基于树的集成方法的讨论中，焦点经常落在标准的优点上:对异常值的健壮性、易于解释等等。但是XGBoost还有其他特性，使其与众不同，并在许多场景中具有优势。

计算效率

通常，围绕XGBoost的讨论都集中在它的预测能力上。不常被强调的是它的计算效率，特别是在并行和分布式计算方面。该算法利用特征和数据点来并行化树结构，使其能够处理更大的数据集，并且比传统实现运行得更快。

缺失数据的处理

XGBoost采用了一种独特的方法来处理缺失值。与其他通常需要单独预处理步骤的模型不同，XGBoost可以在内部处理丢失的数据。在训练过程中，算法为缺失值找到最佳的imputation值(或在树结构中移动的方向)，然后将其存储以供将来预测。这意味着XGBoost处理丢失数据的方法是自适应的，可以因节点而异，从而提供对这些值的更细致的处理。

正则化

虽然增强算法天生就容易过度拟合，特别是对于有噪声的数据，但XGBoost在训练过程中直接将L1 (Lasso)和L2 (Ridge)正则化合并到目标函数中。这种方法提供了一种额外的机制来约束单个树的复杂性，而不是简单地限制它们的深度，从而提高泛化。

稀疏性

XGBoost设计用于高效地处理稀疏数据，而不仅仅是密集矩阵。在使用词袋或TF-IDF表示的自然语言处理等领域，特征矩阵的稀疏性可能是一个重大的计算挑战。XGBoost利用压缩的内存高效数据结构，其算法被设计为有效地遍历稀疏矩阵。

硬件的优化

虽然很少被讨论，但硬件优化是XGBoost的一个亮点。它对CPU上的内存效率和计算速度进行了优化，并支持GPU上的训练模型，进一步加快了训练过程。

特征重要性和模型可解释性

大多数集成方法提供特征重要性度量，包括随机森林和标准梯度增强。但是XGBoost提供了一套更全面的特性重要性度量，包括增益、频率和覆盖范围，从而允许对模型进行更详细的解释。当需要了解哪些特征是重要的，以及它们如何对预测做出贡献时，这一点非常重要。

早停策略

另一个未被讨论的特性是提前停止。谨慎分割和修剪等技术用于防止过拟合，而XGBoost提供了一种更自动化的方法。一旦模型的性能在验证数据集上停止改进，训练过程就可以停止，从而节省了计算资源和时间。

处理分类变量

虽然基于树的算法可以很好地处理分类变量，但是XGBoost采用了一种独特的方法。不需要独热编码或顺序编码，可以让分类变量保持原样。XGBoost对分类变量的处理比简单的二进制分割更细致，可以捕获复杂的关系，而无需额外的预处理。