基础知识
Python函数式编程的主要内容包括以下几个方面:
(1)函数作为一等公民:在函数式编程中,函数被视为一等公民,可以像其他数据类型一样被传递、赋值以及作为返回值。
(2)不可变数据:函数式编程鼓励使用不可变数据,即创建后不能被修改的数据。这使得程序更容易理解和推理,并能减少错误的发生。
(3)纯函数:纯函数是指没有副作用并且对于给定的输入总是产生相同的输出的函数。纯函数不依赖于和修改外部状态,因此更容易进行测试和并发处理。
(4)高阶函数:高阶函数是指能够接受一个或多个函数作为参数,并/或者返回一个函数的函数。高阶函数可以用于构建复杂的逻辑和实现代码的重用。
(5)函数组合与柯里化:函数组合是指将多个函数组合成一个新的函数的过程。柯里化是指将一个接受多个参数的函数转化为一系列只接受一个参数的函数。
(6)递归:递归是函数式编程的常用技术之一,通过函数调用自身来解决问题。
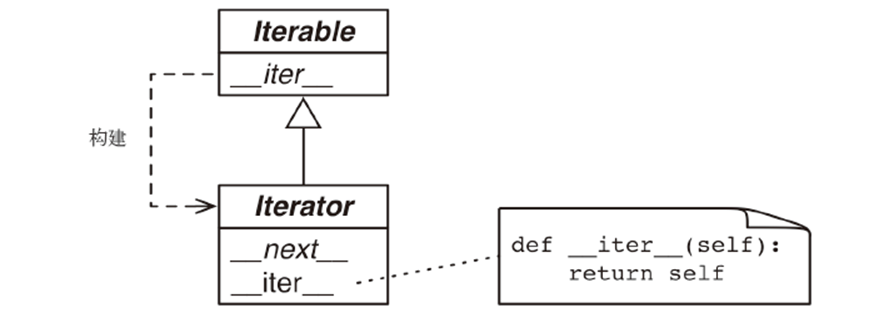
可迭代是指能够被for循环遍历的对象(容器)。
可迭代对象是指实现了__iter__方法的对象,是可以被迭代的对象,例如列表、元组、集合、字典等。
迭代器是实现了无参数的__next__方法,该方法返回序列中的下一个元素;如果没有元素了则抛出StopIteration异常的对象。Python的迭代器还实现了__iter__方法,因此迭代器也可以迭代。
如何创建自己的迭代器?
要自定义一个迭代器,
需要定义一个类并实现__iter__()和__next__()方法。
其中,iter()方法返回迭代器对象本身,
而__next__()方法返回迭代器中的下一个元素。
在迭代器中,可以使用raise StopIteration语句来结束迭代。
如何判断一个对象是否可迭代
判断一个对象是否可迭代,可以使用collections.abc模块中的Iterable类。
具体代码如下:
from collections.abc import Iterable
if isinstance(obj, Iterable):
print('obj是可迭代的')
else:
print('obj不是可迭代的')
惰性求值的主要思想是:只有在需要结果的时候,才进行计算,如果暂时不需要结果,就不进行计算,从而最小化计算机的工作,提高程序的效率
函数参数形式

2.不定长参数:元组(*args)和字典(**kwargs)
可变参数就是传入的参数个数是可变的。
如果一个函数不知道未来要接收多少个参数,可以使用一个元组来接受不定长参数。
def test(*args): # 当成元组的形式来接受参数,一般写成:*args
print(args) # 注意这里的形参不能带*号
print(type(args))
每个参数都用自己的含义,但不是固定参数,可以借用字典的键值对特性来实现
def test(**kwargs): # 当成字典的形式接受参数,一般写成:**kwargs
print(kwargs)
print(type(kwargs))
if __name__ == "__main__":
test(a=3, b=5, c=7)
test(**{‘a’:3, ‘b’:5, ‘c’:7})
3.缺省参数、关键字参数
缺省参数,也称默认值参数,在定义函数的时候,给形参一个默认的值。不传递参数的时候用自己的默认值,传递参数的时候使用传递进去的实参。默认参数应是一个不可变对象
def test(num, str='https://algernon98.github.io/'): #str为缺省参数
print(str * num)
if __name__ == "__main__":
test(num=5) #str使用默认值
test(num=5, str='www') #str使用传递进去的实参
class MyIterator:
def __init__(self, start, end):
self.current = start
self.end = end
def __iter__(self):
return self
def __next__(self):
if self.current > self.end:
raise StopIteration
else:
self.current += 1
return self.current - 1
if __name__ == "__main__":
my_iterator = MyIterator(1, 5)
for i in my_iterator:
print(i)
D:\coder\randomnumbers\venv\Scripts\python.exe D:/coder/randomnumbers/MyIterator.py
1
2
3
4
5
进程已结束,退出代码0
如何判断一个对象是否可迭代
判断一个对象是否可迭代,可以使用collections.abc模块中的Iterable类。
具体代码如下:
from collections.abc import Iterable
if isinstance(obj, Iterable):
print('obj是可迭代的')
else:
print('obj不是可迭代的')
装饰器

import datetime
def log(func):
def printInfo(*arge, **kw): # *不定长参数 **关键字参数
print(' before call ' + func.__name__) # 在调用func之前打印
func(*arge)
print('after call ' + func.__name__) # 在调用func之后打印
return printInfo
@log # 相当于执行了 now = log(now)
def now(astr):
print(astr)
if __name__ == "__main__":
now(datetime.date.today())
D:\coder\randomnumbers\venv\Scripts\python.exe D:/coder/randomnumbers/MyIterator.py
before call now
2023-10-07
after call now
进程已结束,退出代码0
授权验证

授权验证:可以使用装饰器来验证用户的身份和权限,保证系统的安全性。
def requires_auth(f):
def decorated(*args, **kwargs):
auth = request.authorization
if not auth or not check_auth(auth.username, auth.password):
authenticate()
return f(*args, **kwargs)
return decorated
执行函数f前需要认证。
重试机制
重试机制:可以使用装饰器来实现函数执行失败后重试的机制,提高程序的健壮性。
import time
def retry(max_tries=3, delay_seconds=1):
def decorator_retry(func):
def wrapper_retry(*args, **kwargs):
tries = 0
while tries < max_tries:
try:
return func(*args, **kwargs)
except Exception as e:
tries += 1
if tries == max_tries: raise e
time.sleep(delay_seconds)
return wrapper_retry
return decorator_retry
@retry(max_tries=5, delay_seconds=2)
def call_dummy_api():
response = requests.get(“https://jsonplaceholder.typicode.com/todos/1”)
return response
带参数的装饰器
from functools import wraps
def logit(logfile='out.log'):
def logging_decorator(func):
@wraps(func)
def wrapped_function(*args, **kwargs):
log_string = func.__name__ + " was called"
print(log_string)
# 打开logfile,并写入内容
with open(logfile, 'a') as opened_file:
# 现在将日志打到指定的logfile
opened_file.write(log_string + '\n')
return func(*args, **kwargs)
return wrapped_function
return logging_decorator
@logit()
def myfunc1():
Pass
myfunc1() # Output: myfunc1 was called
#现在一个叫做 out.log 的文件出现了,里面的内容就是上面的字符串
@logit(logfile='func2.log')
def myfunc2():
pass
函数
filter()

常用的函数式编程模块
Python中常用的函数式编程模块有:
functools、itertools和operator。
functools模块提供了一些高阶函数,如partial和reduce;
itertools模块提供了各种迭代器工具,如permutations和combinations;
operator模块提供了一些常见的运算符,如add和mul。
这些模块都可以帮助开发者更加方便地实现函数式编程的思想。
operator模块
它包含一组于Python操作符相对应的函数。这些函数在函数式风格的代码中通常很有用,因为它可以替代一些只包括单个操作的函数。
其中的一些函数有:
数学运算:add(),sub(),mul(),div(),floordiv(),abs(),…
逻辑运算:not_(),truth()。
位运算:and_(),or_(),invert()。
对比:eq(),ne(),lt(),le(),gt()和ge()。
对象标识:is_(),is_not()。
functools模块
functools模块包含一些高阶函数。作用:基于已有的函数创建新函数。
高阶函数将一个或多个函数作为输入,并返回一个新的函数。
其中最有用的就是functools.partial()函数。
对函数式风格的程序来说,有时要构建具有填充一些参数的现有函数的变体。比如函数f(a, b, c);你可能希望创建一个新的函数g(b, c),相当于f(1, b, c);这被称之为“部分功能应用程序”。
import functools
def add(a, b):
print(“当前结果值”, a+b)
add = functools.partial(add, 1)
add(2)
递归算法
如果一个算法调用自己来完成它的部分工作,就称这个算法为递归算法。
递归算法必须具有三个部分:
初始情况、递归部分和综合。
初始情况只处理可以直接解决的简单输入;
递归部分包含对算法的一次或多次递归,每次调用的参数在某种程度上比原始调用参数更加接近初始情况。
综合部分把一些小规模问题的解综合为原问题的解。利用递归解决问题的方法就是想办法把一个规模大的问题转换为一个本质相同但规模比较小的问题,
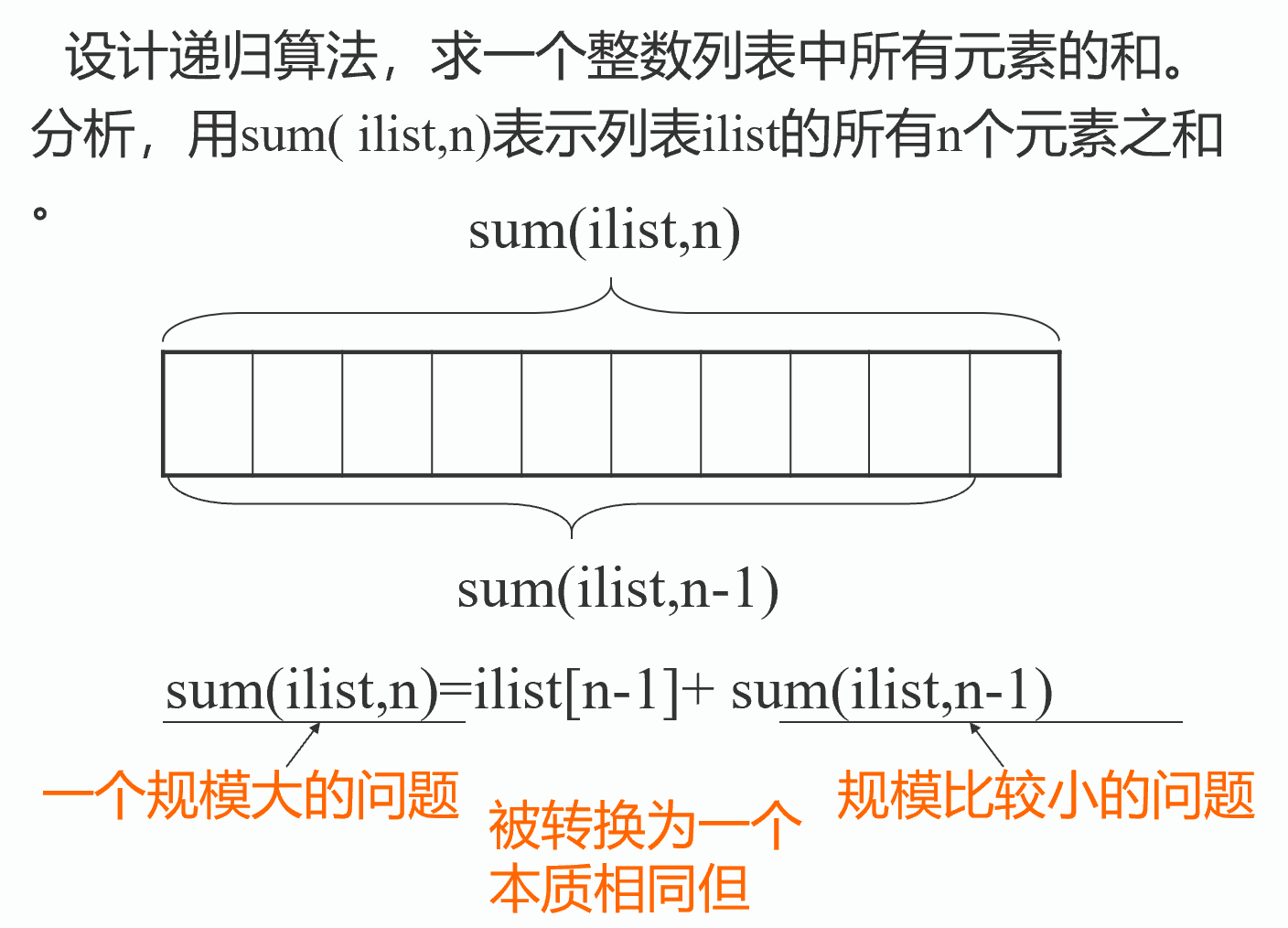
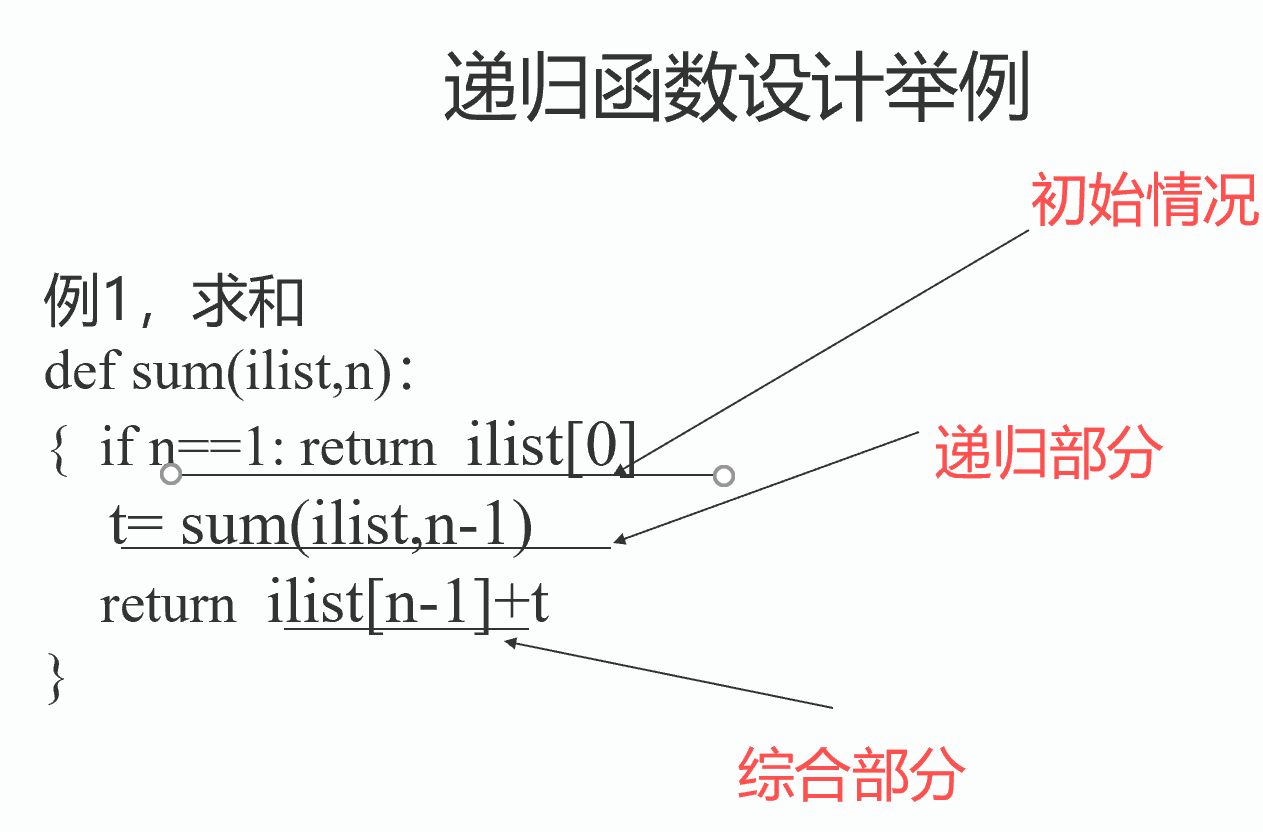
数列求和
def sum(ilist,n):
if n==1:
return ilist[0]
t= sum(ilist,n-1)
return ilist[n-1]+t
list=[1,2,3,4,5,6,7,8,9,10]
print(sum(list,1))
print(sum(list,5))
print(sum(list,10))
D:\coder\randomnumbers\venv\Scripts\python.exe D:/coder/randomnumbers/MyIterator.py
1
15
55
进程已结束,退出代码0
计算阶乘
def rfact( n):
if n<=1:
return 1 #初始情况,直接处理
return n*rfact(n-1) #递归调用与综合
print(rfact(1))
print(rfact(5))
print(rfact(10))
D:\coder\randomnumbers\venv\Scripts\python.exe D:/coder/randomnumbers/MyIterator.py
1
120
3628800
进程已结束,退出代码0
汉诺塔
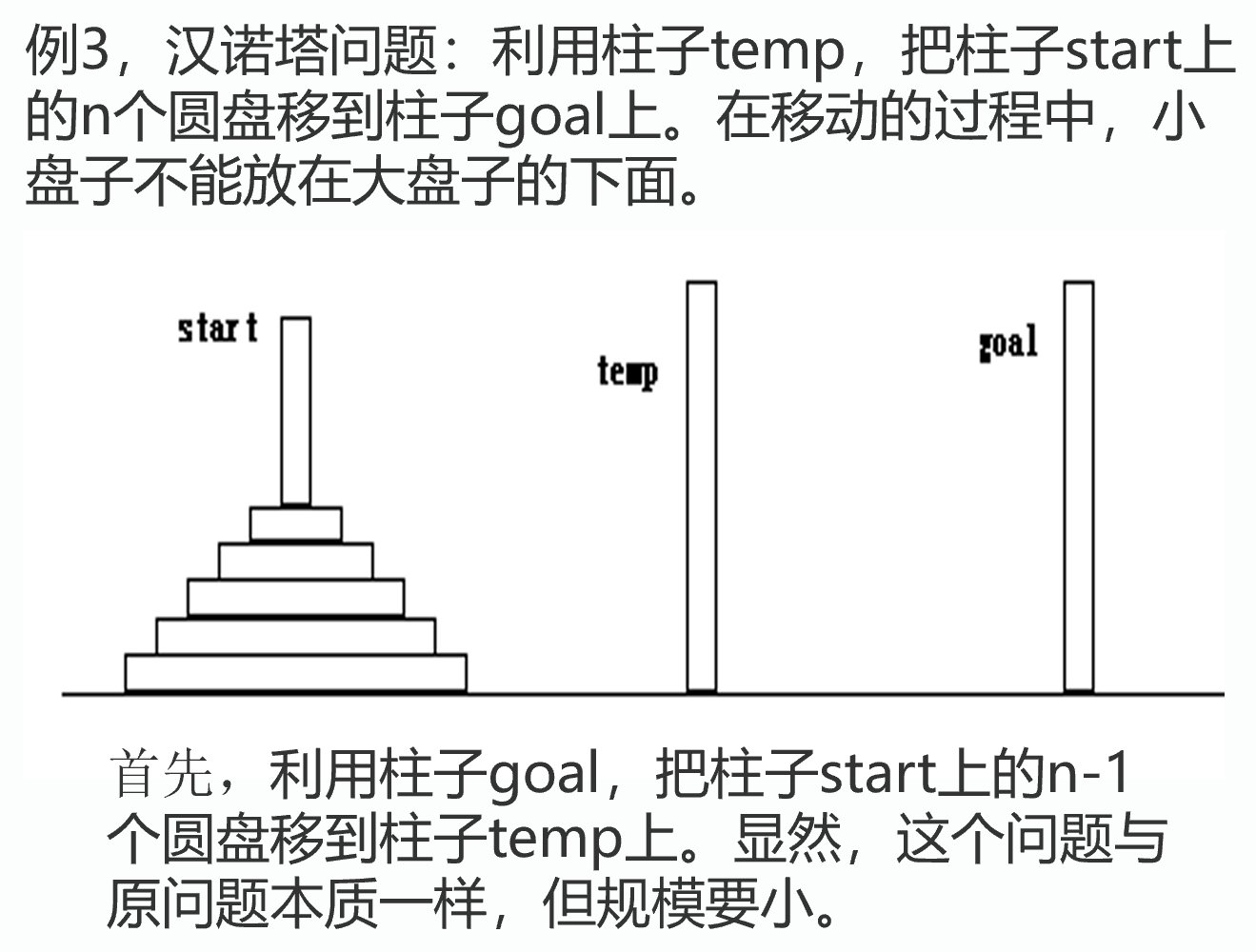
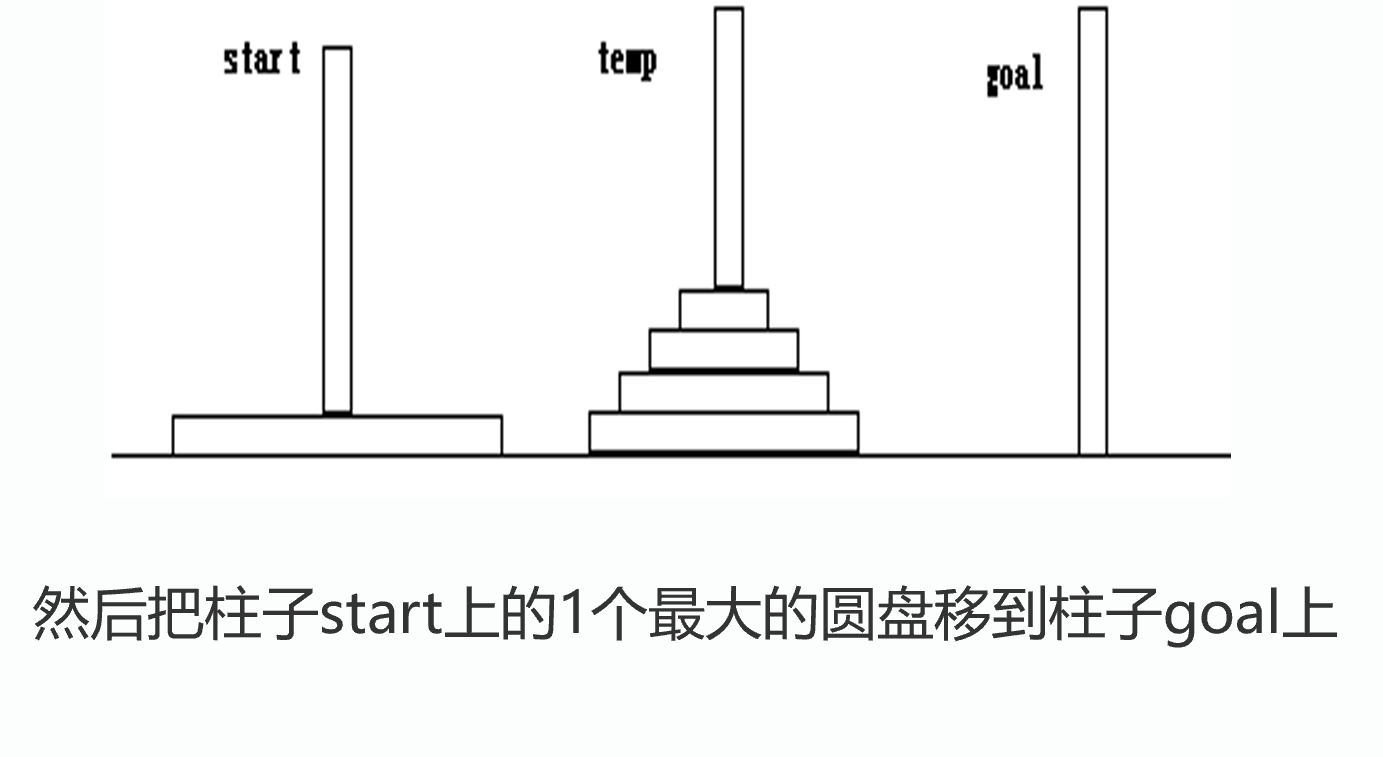
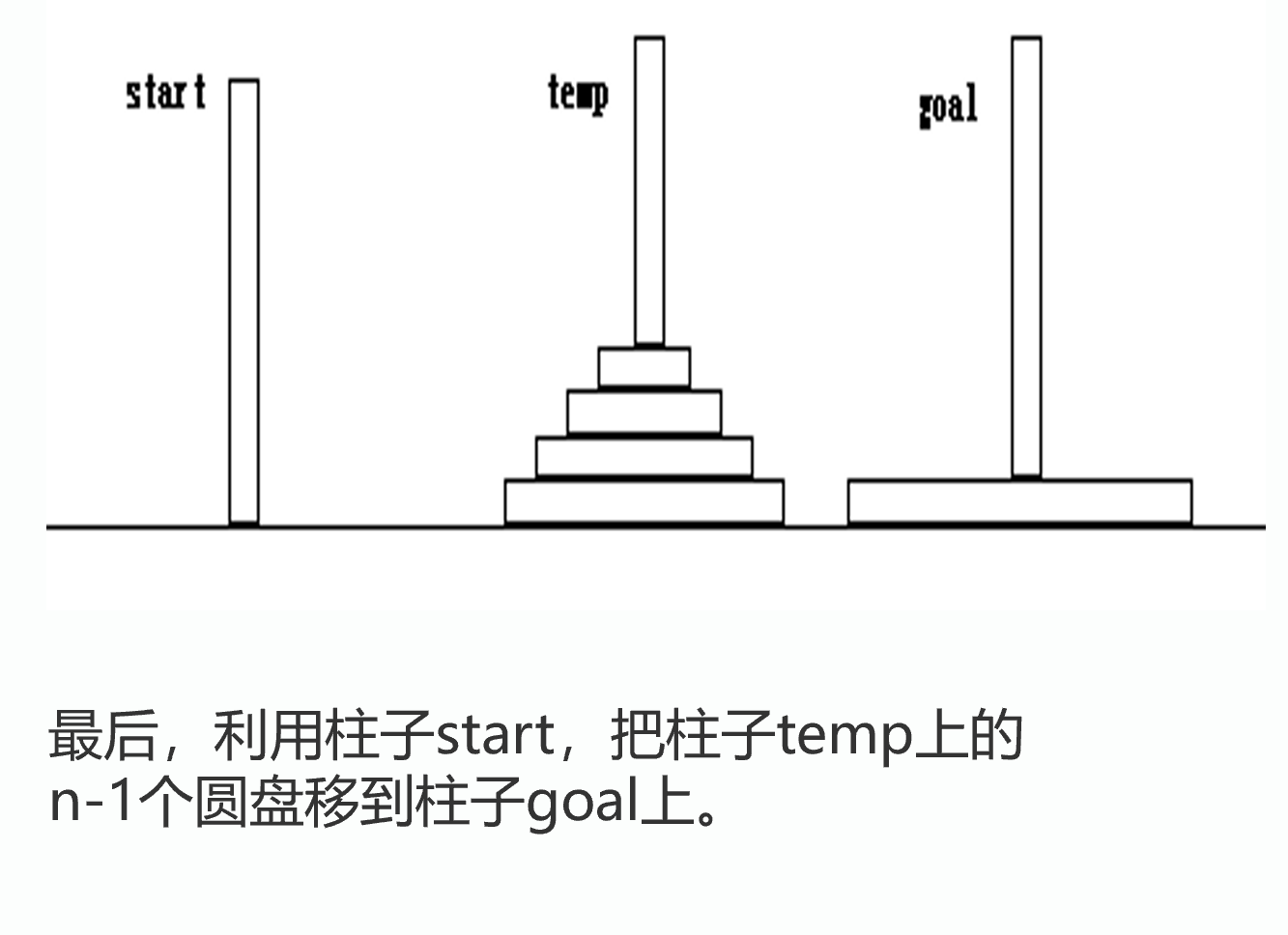
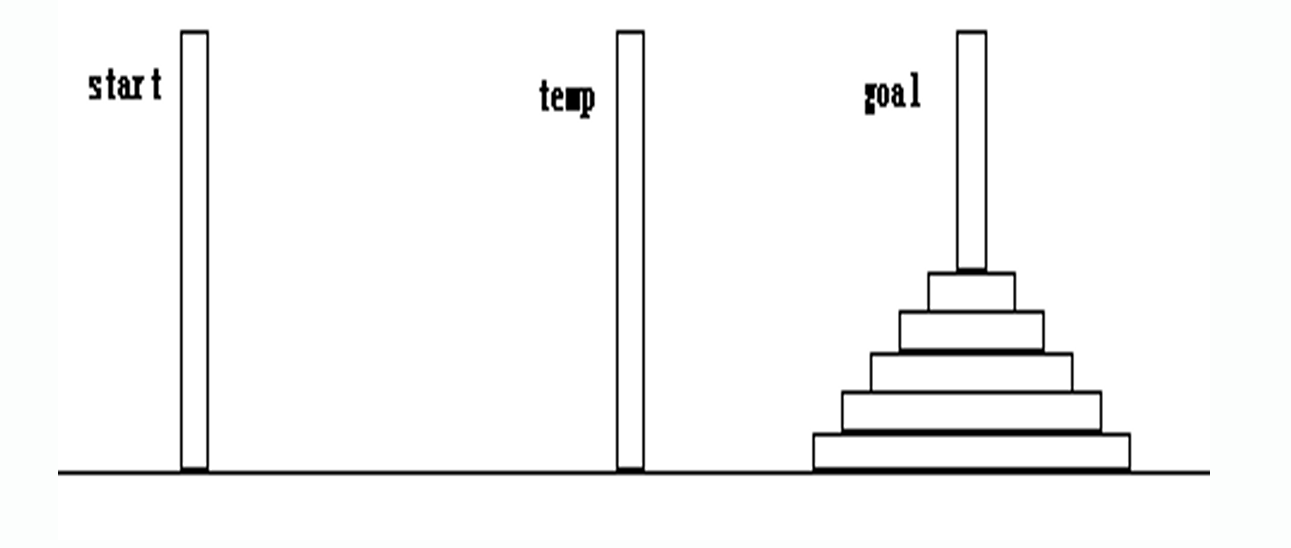
用hanoi(int n,Pole start,Pole goal ,Pole temp)描述:利用柱子temp,把柱子start上的n个圆盘移到柱子goal上.
用move(start,goal)描述把柱子start上的1个最大的圆盘移到柱子goal上。则有
def hanoi(n, start, goal, temp):
if n == 0: return
hanoi(n - 1, start, temp, goal)
move(start, goal)
hanoi(n - 1, temp, goal, start)
def move(start, goal):
print(start, '--->', goal)
hanoi(5, 'start', 'goal', 'temp')
D:\coder\randomnumbers\venv\Scripts\python.exe D:/coder/randomnumbers/MyIterator.py
start ---> goal
start ---> temp
goal ---> temp
start ---> goal
temp ---> start
temp ---> goal
start ---> goal
start ---> temp
goal ---> temp
goal ---> start
temp ---> start
goal ---> temp
start ---> goal
start ---> temp
goal ---> temp
start ---> goal
temp ---> start
temp ---> goal
start ---> goal
temp ---> start
goal ---> temp
goal ---> start
temp ---> start
temp ---> goal
start ---> goal
start ---> temp
goal ---> temp
start ---> goal
temp ---> start
temp ---> goal
start ---> goal
进程已结束,退出代码0
例题
猜数
def decorator(func):
def wrapper_retry(*args, **kwargs):
while True:
result = func(*args, **kwargs)
if result != 'continue':
break
return result
return wrapper_retry
@decorator
def call_dummy_api(n):
x = input("请输入一个数:")
if int(x) > n:
print('big')
return 'continue'
elif int(x) < n:
print('small')
return 'continue'
elif int(x) == n:
print('ok')
return 'yes'
if __name__=="__main__":
call_dummy_api(2)
if __name__ == "__main__":
import random
n=random.randint(30,40)
call_dummy_api(n)
筛选回文
筛选回文 找出在11到200 之间的回文
def is_palindrone(n):
return str(n) == str(n)[::-1] #[::-1]是倒切 从右往左
print( list( filter( is_palindrone, range(11,200) ) ) )
使用python编写一个函数,函数参数为字符串str,函数返回字符串str中最长的回文子串 。
下面的代码找出了给定字符串的所有回文子串
def is_palindrone(s):
return s == s[::-1]
tstr='abcba'
strs=(tstr[pos:pos+length]
for length in range(2,len(tstr)+1)
for pos in range(0,len(tstr)-length+1))
print(list(filter(is_palindrone, strs)))
随机分形
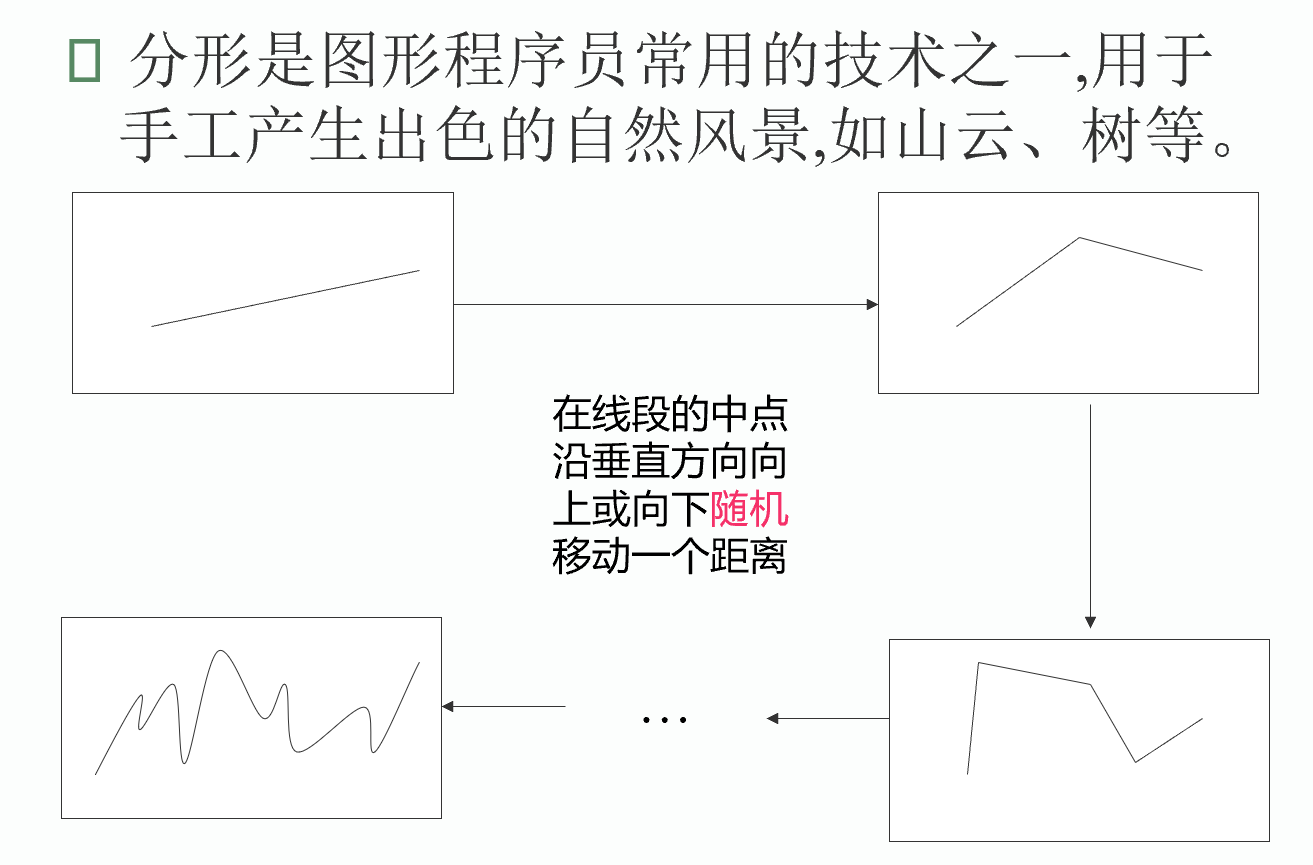
import random
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.sans-serif"]=["SimHei"] #设置显示中文字体
mpl.rcParams["axes.unicode_minus"]=False #设置正常显示符号
def randomFractal(leftX,leftY,rightX,rightY):
STOP = 4
if (rightX - leftX) <= STOP:
plt.plot([leftX, rightX], [leftY, rightY])
else:
midX = (leftX + rightX) / 2
midY = (leftY + rightY) / 2
delta = int(((random.random() - 0.5) * (rightX - leftX)))
midY += delta;
randomFractal(leftX, leftY, midX, midY)
randomFractal(midX, midY, rightX, rightY)
plt.figure(figsize=(8,4),dpi=300) #设置画布大小,图像分辨率
randomFractal(100,400,400,400)
plt.show()
汉诺塔
用hanoi(int n,Pole start,Pole goal ,Pole temp)描述:利用柱子temp,把柱子start上的n个圆盘移到柱子goal上.
用move(start,goal)描述把柱子start上的1个最大的圆盘移到柱子goal上。则有
def hanoi( n,start,goal ,temp):
if n==0: return;
hanoi(n-1,start,temp,goal)
move(start,goal)
hanoi(n-1,temp,goal,start)
def move(start,goal):
print(start,'--->',goal)
hanoi( 5,'start','goal' ,'temp')
求斐波那契数列第n项
def fib( n)
{ if n==1||n==2: return 1 #初始条件
k1=fib(n-1) #递归调用
k2=fib(n-2) #递归调用
return k1+k2 #组合
}
计算n的阶乘
def rfact( n):
if n<=1:
return 1 #初始情况,直接处理
return n*rfact(n-1) #递归调用与综合
print(rfact(5))#以5的阶乘为例
农夫过河
利用python函数式编程,编写程序模拟农夫过河(3只羊和3只狮子过河,有1艘船只能容纳2只动物,当河岸上狮子数大于羊数,羊就会被吃掉,找到运输方法,让所有动物都过河。
from itertools import combinations
def is_safe(state):
# 检查当前状态是否安全
left_bank = state['left']
right_bank = state['right']
if left_bank['lion'] > left_bank['sheep'] > 0 or right_bank['lion'] > right_bank['sheep'] > 0:
return False
return True
def move(state, action):
# 根据动作移动动物到对岸
new_state = {'left': state['left'].copy(), 'right': state['right'].copy()}
boat = state['boat']
if boat == 'left':
for animal in action:
new_state['left'][animal] -= 1
new_state['right'][animal] += 1
new_state['boat'] = 'right'
else:
for animal in action:
new_state['right'][animal] -= 1
new_state['left'][animal] += 1
new_state['boat'] = 'left'
return new_state
def generate_actions(state):
# 生成可行的动作
actions = []
bank = state['left'] if state['boat'] == 'left' else state['right']
for num_animals in range(1, min(3, sum(bank.values())) + 1):
for combination in combinations(bank.keys(), num_animals):
actions.append(combination)
return actions
def solve(state):
# 递归解决问题
if not is_safe(state):
return None
if sum(state['right'].values()) == 6:
return [state]
actions = generate_actions(state)
for action in actions:
new_state = move(state, action)
result = solve(new_state)
if result:
return [state] + result
return None
# 初始状态:3只羊和3只狮子在左岸,船在左岸
initial_state = {'left': {'sheep': 3, 'lion': 3}, 'right': {'sheep': 0, 'lion': 0}, 'boat': 'left'}
# 解决问题
solution = solve(initial_state)
# 打印解决方案
if solution:
for i, state in enumerate(solution):
print(f"Step {i}: {state}")
else:
print("No solution found.")
这个程序使用递归的方式来解决农夫过河问题。它定义了几个辅助函数来检查状态是否安全、移动动物到对岸、生成可行的动作,并使用这些函数来解决问题。最后,它打印出解决方案的每个步骤。
请注意,由于这个问题的状态空间很大,程序可能需要一些时间来找到解决方案。如果没有找到解决方案,它将打印"No solution found."。
改善:
from pythonds.graphs import Graph
from pythonds.basic import Queue
def solution():
'''
3只羚羊和3只狮子过河问题:
1艘船只能容纳2只动物
当河岸上狮子数大于羚羊数,羚羊就会被吃掉
找到运输方法,让所有动物都过河
'''
# 定义合法的运输操作(i, j) , 例如(1, 0)表示运送羚羊1只,狮子0只
opt = [(1, 0), (0, 1), (1, 1), (2, 0), (0, 2)]
# 定义状态state(m, n, k), m表示羚羊数,n表示狮子数,k表示船在此岸还是彼岸
# stateA 表示A岸(此岸)的状态;stateB 表示B岸(彼岸)的状态;
# 初始状态
stateA = (3, 3, 1)
stateB = (0, 0, 0)
# BFS搜索
mygraph = Graph()
myqueue = Queue()
myqueue.enqueue((stateA, stateB))
sequence = [] # 剪枝记录(最后发现,有效状态只有15种)
sequence.append((stateA))
while True:
stateA, stateB = myqueue.dequeue()
if stateA == (0, 0, 0):
break
for o in opt:
# 一次从某岸到另一岸的运输
if stateA[2] == 1:
stateA_ = (stateA[0] - o[0], stateA[1] - o[1], stateA[2] - 1)
stateB_ = (stateB[0] + o[0], stateB[1] + o[1], stateB[2] + 1)
else:
stateB_ = (stateB[0] - o[0], stateB[1] - o[1], stateB[2] - 1)
stateA_ = (stateA[0] + o[0], stateA[1] + o[1], stateA[2] + 1)
# 运输后
if stateA_[0] and stateA_[0] < stateA_[1]: # 此岸在有羊的情况下,如果狼大于羊,则吃掉
continue
elif stateB_[0] and stateB_[0] < stateB_[1]: # 彼岸在有羊的情况下,如果狼大于羊,则吃掉
continue
elif stateA_[0] < 0 or stateA_[0] > 3 or stateA_[1] < 0 or stateA_[1] > 3: # 边界
continue
else:
# 剪枝
if stateA_ in sequence:
continue
else:
sequence.append(stateA_)
myqueue.enqueue((stateA_, stateB_))
mygraph.addEdge(stateA, stateA_, o)
return mygraph, sequence
if __name__ == '__main__':
g, sq = solution()
# 建立父子关系
for v_n in sq:
v = g.getVertex(v_n)
for nbr in v.getConnections():
if nbr.getColor() == 'white':
nbr.setPred(v)
nbr.setColor('gray')
v.setColor('black')
target = g.getVertex(sq[-1])
# 回溯,显示决策路径
while target.getPred():
predv = target.getPred()
print(target.id, '<--', predv.getWeight(target), '--', predv.id)
target = predv
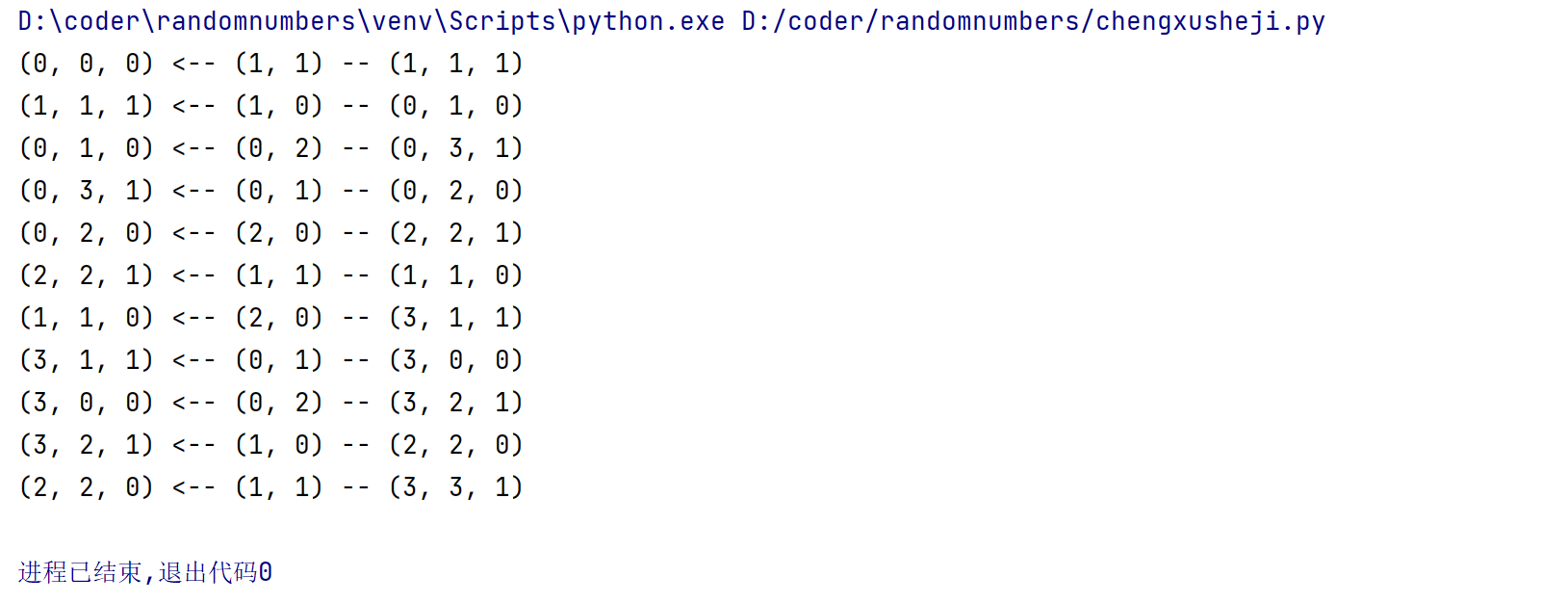
输出:
(0, 0, 0) <-- (1, 1) -- (1, 1, 1)
(1, 1, 1) <-- (1, 0) -- (0, 1, 0)
(0, 1, 0) <-- (0, 2) -- (0, 3, 1)
(0, 3, 1) <-- (0, 1) -- (0, 2, 0)
(0, 2, 0) <-- (2, 0) -- (2, 2, 1)
(2, 2, 1) <-- (1, 1) -- (1, 1, 0)
(1, 1, 0) <-- (2, 0) -- (3, 1, 1)
(3, 1, 1) <-- (0, 1) -- (3, 0, 0)
(3, 0, 0) <-- (0, 2) -- (3, 2, 1)
(3, 2, 1) <-- (1, 0) -- (2, 2, 0)
(2, 2, 0) <-- (1, 1) -- (3, 3, 1)
随机生成中国人姓名
import random
def generate_chinese_name():
# 常见的姓氏
surnames = ['赵', '钱', '孙', '李', '周', '吴', '郑', '王', '冯', '陈', '褚', '卫', '蒋', '沈', '韩', '杨', '朱', '秦', '尤', '许', '何', '吕', '施', '张', '孔', '曹', '严', '华', '金', '魏', '陶', '姜', '戚', '谢', '邹', '喻', '柏', '水', '窦', '章', '云', '苏', '潘', '葛', '奚', '范', '彭', '郎', '鲁', '韦', '昌', '马', '苗', '凤', '花', '方', '俞', '任', '袁', '柳', '酆', '鲍', '史', '唐', '费', '廉', '岑', '薛', '雷', '贺', '倪', '汤', '滕', '殷', '罗', '毕', '郝', '邬', '安', '常', '乐', '于', '时', '傅', '皮', '卞', '齐', '康', '伍', '余', '元', '卜', '顾', '孟', '平', '黄', '和', '穆', '萧', '尹', '姚', '邵', '湛', '汪', '祁', '毛', '禹', '狄', '米', '贝', '明', '臧', '计', '伏', '成', '戴', '谈', '宋', '茅', '庞', '熊', '纪', '舒', '屈', '项', '祝', '董', '梁', '杜', '阮', '蓝', '闵', '席', '季', '麻', '强', '贾', '路', '娄', '危']
# 常见的名字
names = ['伟', '芳', '娜', '秀英', '敏', '静', '丽', '强', '磊', '洋', '艳', '勇', '军', '杰', '娟', '涛', '明', '超', '秀兰', '霞', '平', '刚', '桂英', '英', '华', '民', '强', '燕', '平', '鹏', '飞', '慧', '红', '宇', '建华', '建国', '建军', '云', '亮', '志强', '志伟', '志刚', '志勇', '志明', '志平', '志杰', '志文', '志国', '志强', '志伟', '志刚', '志勇', '志明', '志平', '志杰', '志文', '志国', '志强', '志伟', '志刚', '志勇', '志明', '志平', '志杰', '志文', '志国', '志强', '志伟', '志刚', '志勇', '志明', '志平', '志杰', '志文', '志国']
surname = random.choice(surnames)
name = random.choice(names)
return surname + name
# 生成一个随机的中国人名字
chinese_name = generate_chinese_name()
print(chinese_name)
这个生成函数使用了常见的姓氏和名字列表,然后通过random.choice()函数随机选择一个姓氏和一个名字进行组合。最后,它返回生成的中国人名字。








![[GXYCTF 2019]Ping Ping Ping题目解析](https://img-blog.csdnimg.cn/556000ec835f4ff5811087f5604ab94e.png)