167. 两数之和 II - 输入有序数组 - 力扣（LeetCode）

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列  ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

示例 2：

输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

示例 3：

输入：numbers = [-1,0], target = -1
输出：[1,2]
解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

>>思路和分析：(举个栗子)

① 暴力破解

② 双指针解法，本文着重讲此方法：

这里的2+8=10>9，且由于是有序数组，势必在范围(left,right)中的任意一数与right所指之数之和一定大于9。此时需要让right--，才有可能找到题目所求

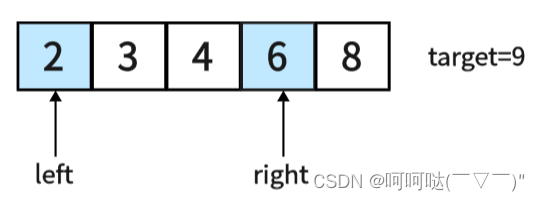
这里的2+6=8<9，且由于是有序数组，势必在范围(left,right)中的任意一数与left所指之数之和一定小于9。此时需要让left++，才有可能找到题目所求

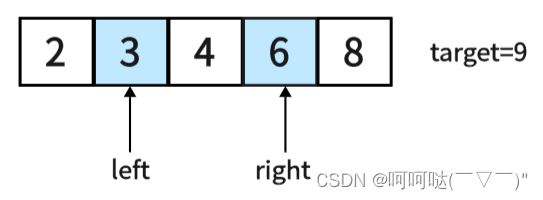
这里的3+6=9，可获得题目所求

• 思考：🤔与暴力破解方法相比，用双指针有什么好处？

注意每次只花费O(1)的时间，把两个数加起来和 target=9 比较大小。我们就通过这个大小关系直接去掉了一个数。每次花费O(1)时间去掉一个数，直到找到答案。因此，这个算法的时间复杂度是O(n)。这相比原来的暴力做法O(n)就是一个巨大的优化。

• 分析：🤔那么这个算法相比暴力解法到底快哪里？

用一个获取多少信息量来衡量一个算法的效率，暴力做法就是找两个数加起来和9比一比。那它花费O(1)的时间就知道了O(1)的信息，而优化之后的做法，是把当前剩下的最小的数和最大的数加起来和9比一比，那比完之后，就知道其中一个数和其他任何一个数相加都是小于9的，或者都是大于9的。那这样我就花费O(1)的时间，就知道了O(n)的信息。那这就是为什么能够从O(n^2)优化到O(n)。

• 思考：🤔这个解法的本质是什么？
  • 其实是缩减搜索空间

注意这一切的前提是数组是排好序的，我们利用了这个性质，如果数组是没有序的，那么我们就不能够使用这个算法，那如何用代码实现呢？可以初始化两个下标，也可以叫指针，用left 和 right，代码如下：

C++代码：

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        int left=0,right = numbers.size()-1;
        while(left<right) {
            int sum = numbers[left] + numbers[right];
            if(sum == target) return {left+1,right+1};
            // else if(sum > target) right--; 
            // else left++;
            sum > target ? --right : ++left; 
        } 
        return {};
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1) 

python代码：

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        # 时间复杂度 O(n)
        # 空间复杂度 O(1)
        left = 0
        right = len(numbers) - 1
        while True: # left < right
            s = numbers[left] + numbers[right]
            if s == target:
                break
            if s > target:
                right-=1
            else:
                left+=1
        return [left+1,right+1]

参考和推荐文章、视频：

167. 两数之和 II - 输入有序数组 - 力扣（LeetCode）

两数之和 三数之和【基础算法精讲 01】_哔哩哔哩_bilibili