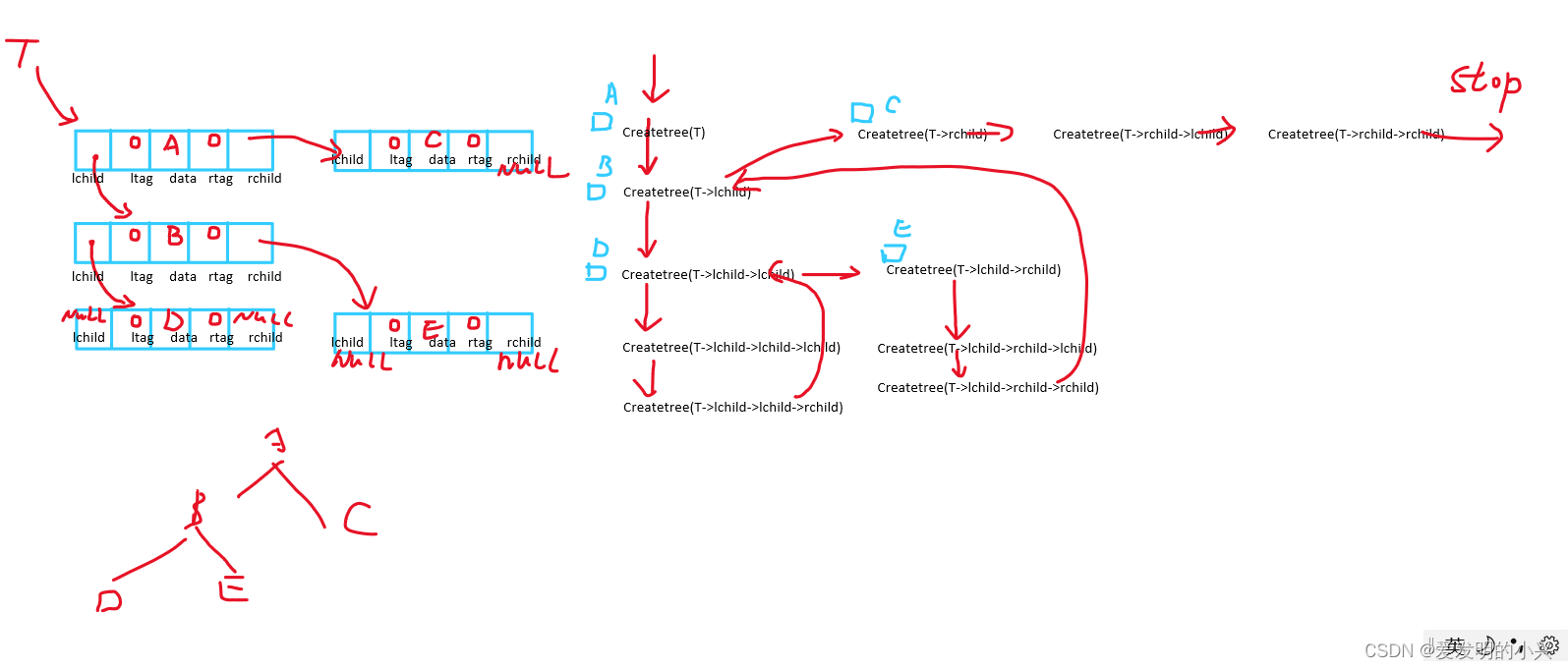
思路:

1. 机器人是完全相同的且移动速度一样，所以对于碰撞后转向的机器人，可以看作是不碰撞继续运动。可以这么理解，如果没有碰撞，在移动后坐标 i 处有一个机器人，那么存在碰撞的情况下，坐标 i 处任有一个机器人，只不过标签不一样，所以在机器人相同的情况下可以视作没有碰撞的情况。
2. 计算所有机器人之间的两两距离之和，暴力遍历的时间复杂度为O(n²)，会超时。
3. 快速求解距离之和，首先假设最左边的机器人坐标为 l，最右边的机器人坐标为 r，那么它们和其他所有机器人的两两距离之和就是 (r - l)*(n-2)，其中 n 为机器人的总数。
4. 在第三步中，我们求出了最旁边两个机器人和其他所有机器人的组合距离之和，那么在接下来的计算过程中将不用再考虑它们，以此类推就可以在排序O(nlogn)+递推O(n)的时间复杂度内完成计算。

class Solution:
    def sumDistance(self, nums: List[int], s: str, d: int) -> int:
        n = len(nums)
        for i in range(n):
            if s[i] is 'R':
                nums[i] += d
            if s[i] is 'L':
                nums[i] -= d

        ans = 0
        nums.sort()
        for i in range(n // 2):
            ans += abs(nums[i] - nums[n - 1 - i]) * (n - 2 * i - 1)
            ans %= 1000000007

        return ans