大家好,我是带我去滑雪!
向量自回归(VAR)模型和误差修正模型(ECM)是时间序列分析中常用的两种模型,它们用于研究多个变量之间的动态关系。VAR 模型适用于研究多个相关变量之间的相互影响和动态关系,特别是在没有明确的因果关系方向时。ECM 是基于向量自回归模型的一种扩展,旨在处理协整关系。协整关系表示变量之间存在长期均衡关系。在实践中,研究人员通常使用单位根检验(如ADF检验)来检查时间序列是否平稳,然后使用协整检验来确定是否存在协整关系。如果存在协整关系,就可以考虑使用 VAR 模型和 ECM 模型来分析变量之间的关系。这些模型在经济学、金融学和其他领域中广泛应用,以揭示变量之间的动态性质和长期均衡关系。
一、向量自回归模型
(1)平稳VAR多变量原理
平稳向量自回归(VAR)模型是一种多变量时间序列分析方法,用于研究变量之间的动态关系。在VAR模型中,所有的变量被同时建模,每一个变量都被其它所有变量的滞后值所影响。这种模型假设所有的变量都是平稳的,也就是说,它们的均值和方差在时间上是稳定的。总的来说,VAR模型的核心思想是将多个变量之间的关系纳入一个系统方程中,通过时间序列的历史数据来估计这些关系,从而实现对未来变量值的预测和分析。VAR模型的基本原理可以总结如下:
-
平稳性假设: VAR模型假设所涉及的所有变量都是平稳的。平稳性是指变量的统计特性,如均值和方差,在时间上保持不变。如果变量不是平稳的,通常需要进行差分操作,直到得到平稳的数据。
-
滞后阶数选择: 在构建VAR模型时,需要选择滞后阶数(lag order),表示当前时刻的变量值受多少时期之前的变量值影响。选择适当的滞后阶数通常需要借助信息准则(如AIC或BIC)来进行。
-
模型参数估计: 一旦选择了滞后阶数,就可以用最小二乘法(OLS)或极大似然法来估计VAR模型的参数。这些参数代表了各个变量之间的线性关系。
-
脉冲响应函数和方差分解: 通过VAR模型,可以得到系统中各个变量对于其它变量脉冲(冲击)的响应模式。脉冲响应函数显示了一个变量在受到一个单位冲击时的反应情况。方差分解则能够量化各个变量在系统变动中所占的比重。
-
预测和融合: 一旦VAR模型被估计出来,就可以用来进行未来数值的预测。此外,VAR模型还可以与其他模型或分析方法融合,以提高预测的准确性。
(2)下载并整理数据,为构建VAR模型做准备
下载数据可以查看前面的博客(http://t.csdnimg.cn/tdjvG),本期使用getSymbls函数从网络上下载IBM从2015年1月1日到2017年1月18日的股票数据,数据包含IBM的开盘价、收盘价、成交量等数据。
install.packages("TTR")
library(quantmod)
IBM.dat = getSymbols("IBM", from="2015-01-01",to="2017-01-18", adjust = T, auto.assign = FALSE)
head(IBM.dat)
tail(IBM.dat)
Return = diff(log(IBM.dat[, 4]))*100
volume = log(IBM.dat[, 5])
plot(Return, xlab = "dates", main = "Time series of IBM returns")
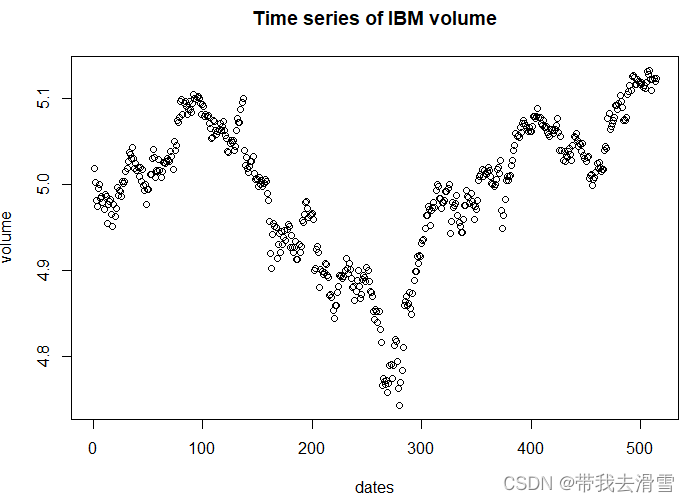
plot(volume, xlab = "dates", main = "Time series of IBM volume")
dat0=cbind(Return, volume)
head(dat0)
dat=na.omit(dat0)输出结果:
(3)估计VAR(p)
library(vars)
out.var=VAR(dat, p=1, type="const", season=NULL, exogen=NULL, lag.max=NULL)
options(digits=4)
coef(out.var)输出结果:
$Return
Estimate Std. Error t value Pr(>|t|)
Return.l 1 0.08745 0.04399 1.988 0.04737
volume.l 1 -1.11633 0.66518 -1.678 0.09391
const 5.59278 3.32232 1.683 0.09291$volume
Estimate Std. Error t value Pr(>|t|)
Return.l 1 0.007989 0.0002939 27.186 2.904e-101
volume.l 1 0.992436 0.0044435 223.347 0.000e+00
const 0.037821 0.0221934 1.704 8.896e-02
(4)Granger因果关系检验
causality(out.var, cause="Return", boot=TRUE, boot.runs=5000)
输出结果:
$Granger
Granger causality H0: Return do not Granger-cause volume
data: VAR object out.var
F-Test = 739, boot.runs = 5000, p-value <2e-16
$InstantH0: No instantaneous causality between: Return and volume
data: VAR object out.var
Chi-squared = 76, df = 1, p-value <2e-16
结果显示,拒绝原假设,认为报酬率是交易量的格兰杰原因。
(5)脉冲响应分析
output.irf=irf(out.var, impulse = "Vol", response = c("Ret","Vol"),boot=TRUE, boot.runs=1000)
output.irf
plot(output.irf)
二、误差修正模型
完整代码如下:
library(tsDyn)
lags <- vars::VARselect(dat, lag.max=25)$selection
vecm.eg<-VECM(dat, lag=lags[3],include ="const", estim = "2OLS")
summary(vecm.eg)
summary(vecm.eg)$coefMat
vecm.eg$model.specific$beta
vecm.jo<-VECM(dat, lag=lags[3], include ="const", estim = "ML")
summary(vecm.jo)
summary(vecm.jo)$coefMat
vecm.jo$model.specific$beta
library(urca)
cointest_eigen <- ca.jo(dat, K=lags[3], type="eigen", ecdet="const",spec="transitory")
summary(cointest_eigen)
cointest_trace <- ca.jo(dat, K=lags[3], type="trace", ecdet="const",spec="transitory")
summary(cointest_trace)
需要数据集的家人们可以去百度网盘(永久有效)获取:
链接:https://pan.baidu.com/s/1E59qYZuGhwlrx6gn4JJZTg?pwd=2138
提取码:2138
更多优质内容持续发布中,请移步主页查看。
点赞+关注,下次不迷路!