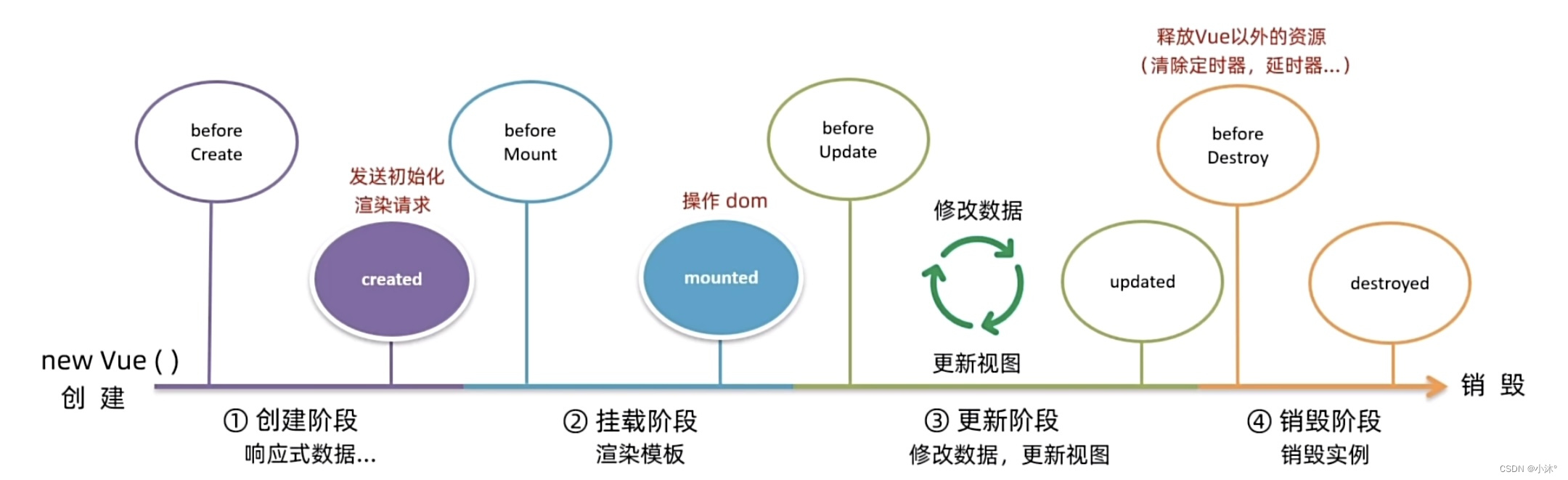
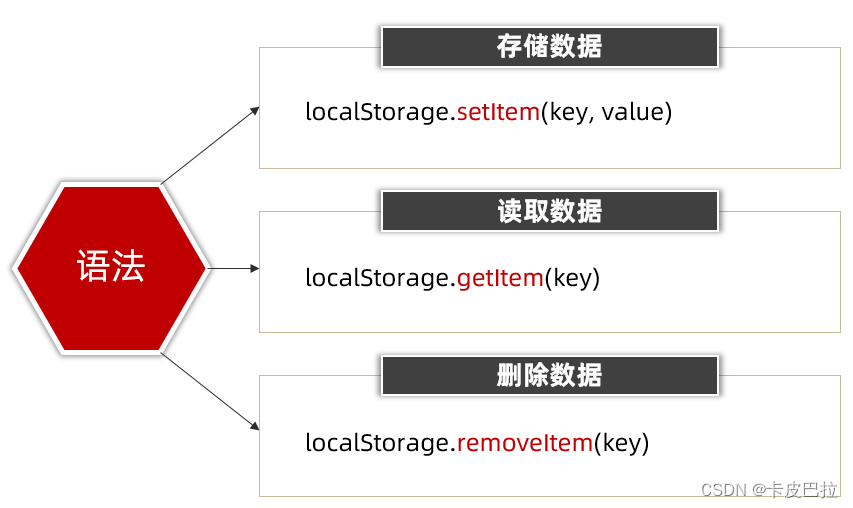
记忆宫殿法
一元二次函数:
y
=
a
x
2
+
b
x
+
c
y=ax^2+bx+c
y=ax2+bx+c
a
>
0
a>0
a>0,开口向上;
a
<
0
a<0
a<0,开口向下;
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab是函数的对称轴;
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab,
y
=
4
a
c
−
b
2
4
a
y=\frac{4ac-b^2}{4a}
y=4a4ac−b2是函数的顶点坐标;
c
=
0
c=0
c=0,一元二次函数图像过坐标原点;
理解记忆法
归类记忆法
一元二次函数公式总结
一般式:
y
=
a
x
2
+
b
x
+
c
(
a
≠
0
)
y=ax^2+bx+c(a≠0)
y=ax2+bx+c(a=0)
配方式/顶点式:
y
=
a
(
x
+
b
2
a
)
2
+
4
a
c
−
b
2
4
a
y=a(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a}
y=a(x+2ab)2+4a4ac−b2,对称轴为
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab,顶点坐标为
(
−
b
2
a
,
4
a
c
−
b
2
4
a
)
(-\frac{b}{2a},\frac{4ac-b^2}{4a})
(−2ab,4a4ac−b2)
两根式:
y
=
a
(
x
−
x
1
)
(
x
−
x
2
)
y=a(x-x_1)(x-x_2)
y=a(x−x1)(x−x2),
x
1
,
x
2
x_1,x_2
x1,x2是函数的两个根,对称轴为
x
=
x
1
+
x
2
2
x=\frac{x_1+x_2}{2}
x=2x1+x2
求根公式:
x
12
=
−
b
±
b
2
−
4
a
c
2
a
x_{12}=\frac{-b±\sqrt{b^2-4ac}}{2a}
x12=2a−b±b2−4ac
判别式:
△
=
b
2
−
4
a
c
△=b^2-4ac
△=b2−4ac
韦达定理:
x
1
+
x
2
=
−
b
a
x_1+x_2=-\frac{b}{a}
x1+x2=−ab,
x
1
⋅
x
2
=
c
a
x_1·x_2=\frac{c}{a}
x1⋅x2=ac【注意用韦达定理之前验证判别式大于等于零】
弦长公式:若
y
=
a
x
2
+
b
x
+
c
(
a
≠
0
)
y=ax^2+bx+c(a≠0)
y=ax2+bx+c(a=0),当
△
=
b
2
−
4
a
c
>
0
△=b^2-4ac>0
△=b2−4ac>0时,函数图像与x轴有两个交点
A
(
x
1
,
0
)
A(x_1,0)
A(x1,0),
B
(
x
2
,
0
)
B(x_2,0)
B(x2,0),则
∣
A
B
∣
|AB|
∣AB∣=
∣
x
1
−
x
2
∣
|x_1-x_2|
∣x1−x2∣=
△
∣
a
∣
\frac{\sqrt{△}}{|a|}
∣a∣△
顶点三角形面积公式:若
y
=
a
x
2
+
b
x
+
c
y=ax^2+bx+c
y=ax2+bx+c与
x
x
x轴有两个交点A,B,顶点为P,则
S
△
A
B
P
=
(
△
)
3
8
a
2
S_{△ABP}=\frac{(\sqrt{△})^3}{8a^2}
S△ABP=8a2(△)3
重点记忆法
△ △ △判别式 ⟹ \Longrightarrow ⟹ b 2 − 4 a c b^2-4ac b2−4ac ⟹ \Longrightarrow ⟹ △ △ △>0, x x x= − b ± △ 2 a \frac{-b±\sqrt{△}}{2a} 2a−b±△,抛物线与x轴有两个交点 ⟹ \Longrightarrow ⟹ △ △ △=0, x x x为 − b 2 a -\frac{b}{2a} −2ab,抛物线与x轴有一个交点 ⟹ \Longrightarrow ⟹ △ △ △<0,抛物线与x轴没有交点 ⟹ \Longrightarrow ⟹ y y y的最值 4 a c − b 2 4 a \frac{4ac-b^2}{4a} 4a4ac−b2 = -△ 4 a \frac{-△}{4a} 4a-△
数字编码法
1.一元二次方程
a
x
2
+
b
x
+
c
=
0
ax^2+bx+c=0
ax2+bx+c=0:
根判别式:
△
=
b
2
−
4
a
c
△=b^2-4ac
△=b2−4ac:跟盘别试,比尔见识苹果月亮
根:
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab:阿克斯,伏笔除二苹果。伏笔初二苹果。阿克斯伏笔出一二苹果。阿克思福必出一二苹果。
2.二次函数
y
=
a
x
2
+
b
x
+
c
y=ax^2+bx+c
y=ax2+bx+c:
最值:
y
=
4
a
c
−
b
2
4
a
y=\frac{4ac-b^2}{4a}
y=4a4ac−b2:外,死苹果月亮见比尔厨艺死苹果。死苹果见比尔出一丝苹果 。

根判别式=笔方-4个苹果月亮=笔儿见死苹果月亮
比尔见识苹果月亮
转图像记忆法
结合字母编码
学习记忆——英语——字母编码
- 一元二次方程的根:
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab:2座桥,桥上有一个香蕉,桥底有两个苹果。
或者:两颗苹果上面有根香蕉,要想托稳香蕉,得有两个横版(一个负号,一个除号)。

或者两个苹果上面有一座桥和一根香蕉

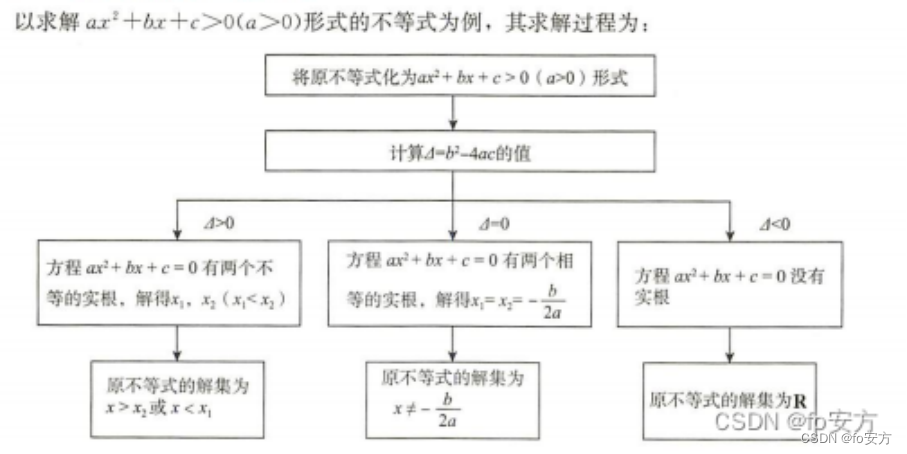
2.
y
=
a
x
2
+
b
x
+
c
y=ax^2+bx+c
y=ax2+bx+c的最值:
4
a
c
−
b
2
4
a
\frac{4ac-b^2}{4a}
4a4ac−b2 =—
△
4
a
\frac{△}{4a}
4a△
4颗苹果上面有两座桥,桥上有一个三角形。


- 韦达定理
x为剪刀,a苹果,b香蕉,c月亮
剪头➕剪刀可以换,苹果顶着负香蕉
剪刀,剪刀,剪刀,可以换,苹果顶着月亮