算法错题簿（持续更新）

自用算法错题簿，按算法与数据结构分类

python
- 1、二维矩阵：记忆化搜索dp
- 2、图论：DFS
- 3、回溯：1296=1+29+6
- 4、二叉树：贪心算法
- 5、字符串：记忆化搜索
- 6、01字符串反转：结论题
- 7、二进制数：逆向思考问题，对结果进行遍历
- 8、求质数：list和set的区别
- 9、滑动窗口：求子数组个数
- 10、最大子数组：DFS+遍历
- 11、字符串和字符串数组：遍历查找技巧
go
- 1、01背包，快速幂计算
- 2、字符串组合
- 3、数位dp，模拟记忆化搜索，位运算
- 4、多源BFS，并查集
- 5、有序队列
- 6、线性dp
- 7、对数组至多删除k个元素，求子数组最大值
- 8、前缀和
- 9、矩阵处理，全排列
- 10、前缀最大值、后缀最大值

python

1、二维矩阵：记忆化搜索dp

在这里插入图片描述

class Solution:
    def maxMoves(self, grid: List[List[int]]) -> int:
        m,n=len(grid),len(grid[0])
        @cache
        def dfs(i:int,j:int) -> int:
            if j == n-1 : return 0
            res = 0
            for k in i-1,i,i+1:
                if 0 <= k < m and grid[k][j+1] > grid[i][j]:
                    res = max(res, dfs(k,j+1)+1)
            return res
        return max(dfs(i,0) for i in range(m))

这里的@cache是记忆化搜索，如果传入相同的参数，则会直接输出结果，如下图时间对比

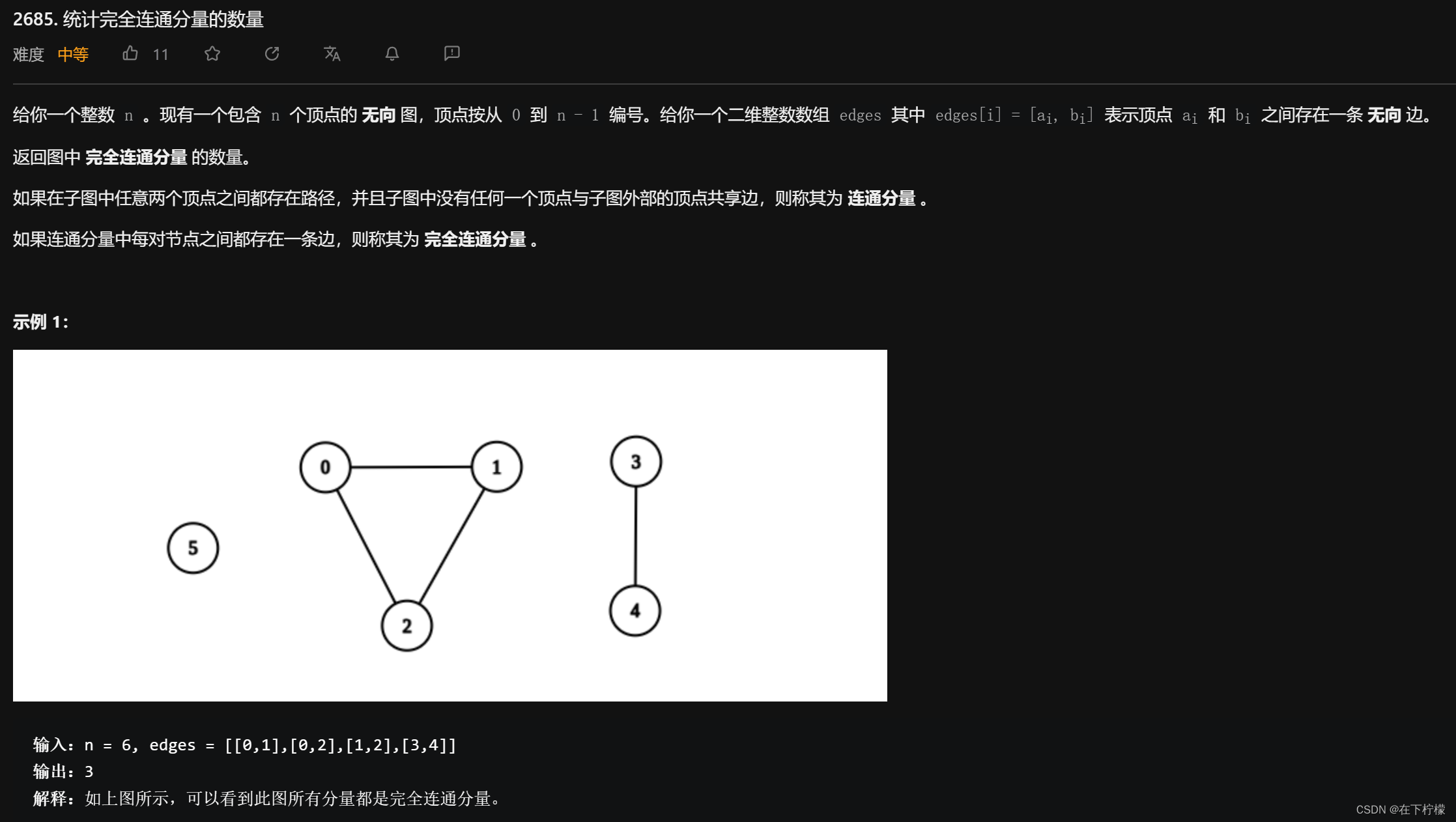
2、图论：DFS

在这里插入图片描述

class Solution:
    def countCompleteComponents(self, n: int, edges: List[List[int]]) -> int:
        g = [[] for _ in range(n)]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)

        vis = [False] * n
        def dfs(x: int) -> None:
            vis[x] = True
            nonlocal v, e
            v += 1
            e += len(g[x])
            for y in g[x]:
                if not vis[y]:
                    dfs(y)

        ans = 0
        for i, b in enumerate(vis):
            if not b:
                # 点数v，边数e
                v = e = 0
                dfs(i)
                ans += e == v * (v - 1)
        return ans

python的建表方法，比较固定
对于一个完全连通分量，点数v，边数e，有e == v*(v - 1)/2，所以代码中，在dfs中对每个点都加上连接点数，再遍历与其连接的点，这样对于一个完全图上每个点连接的边都会被记录两次，最后与v*(v-1)进行比较，如果小了，那这个圆就没有闭合，如果大了，那这个圆就和其他点有边。
nonlocal可以让python在方法中使用方法定义之后出现的变量

3、回溯：1296=1+29+6

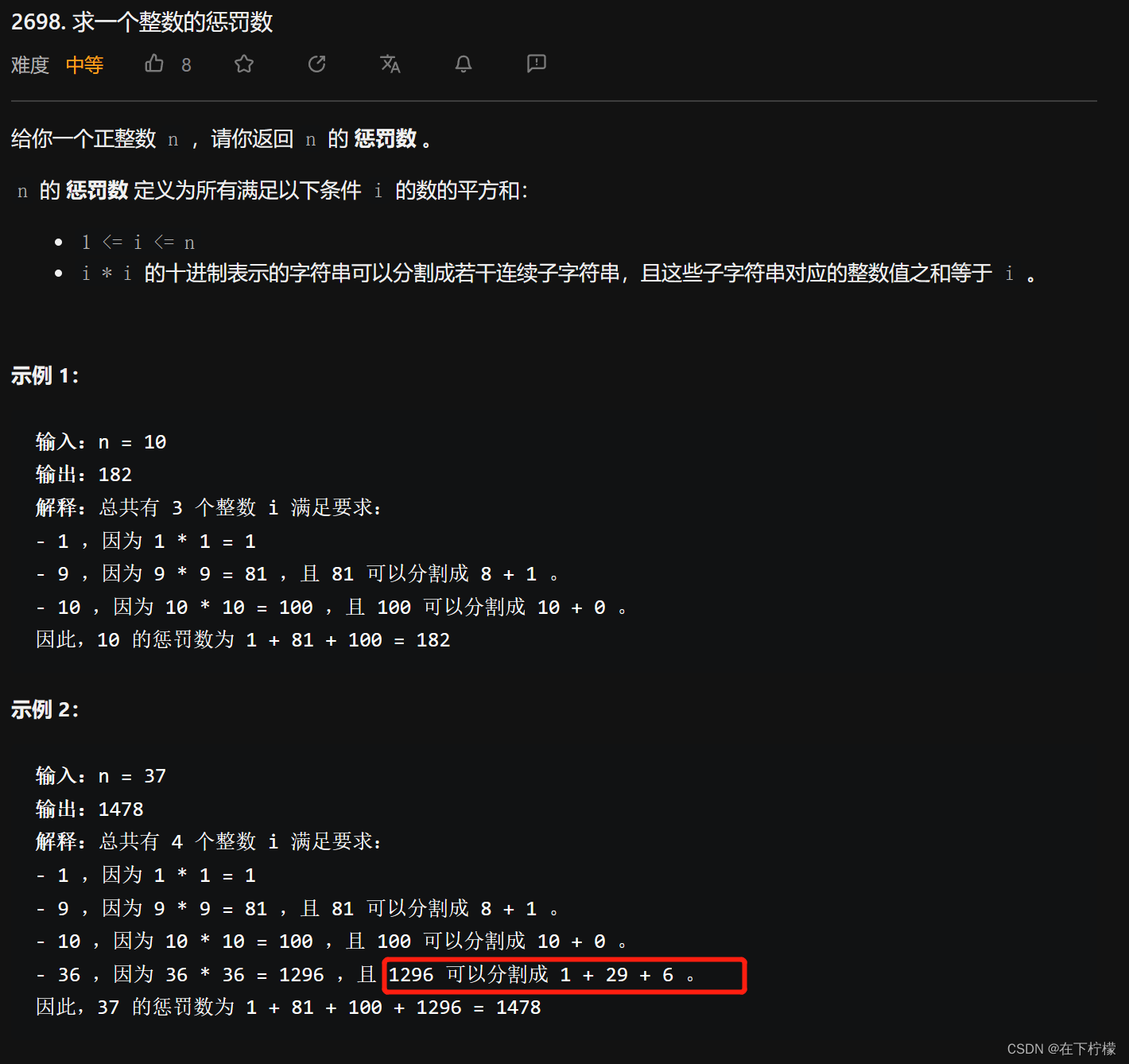
在这里插入图片描述

数字范围1<=n<=1000

这道题的难点在于，如何将一个数字分割成所有可能的情况，从中选出符合条件的情况，并且不超时

答案是回溯

ok = [False] * 1001
for i in range(1,1001):
    s = str(i*i)
    n = len(s)
    def dfs(p:int,sum:int) -> bool:
        if p == n:
            return sum == i
        x = 0
        for j in range(p, n):
            x = x*10+int(s[j])
            # 剪枝操作
            if dfs(j+1,sum+x):
                return True
        return False
    ok[i] = dfs(0,0)

class Solution:
    def punishmentNumber(self, n: int) -> int:
        res = 0
        for i in range(n+1):
            if ok[i]:
                res+=i*i
        return res

数据值比较小，只有1000，所以可以直接写在外面，每次调用Solution的时候直接从数组中查就可以
代码中写函数可以使用函数定义之前的变量，但是如果要使用定义之后的值，需要用nonlocal修饰

4、二叉树：贪心算法

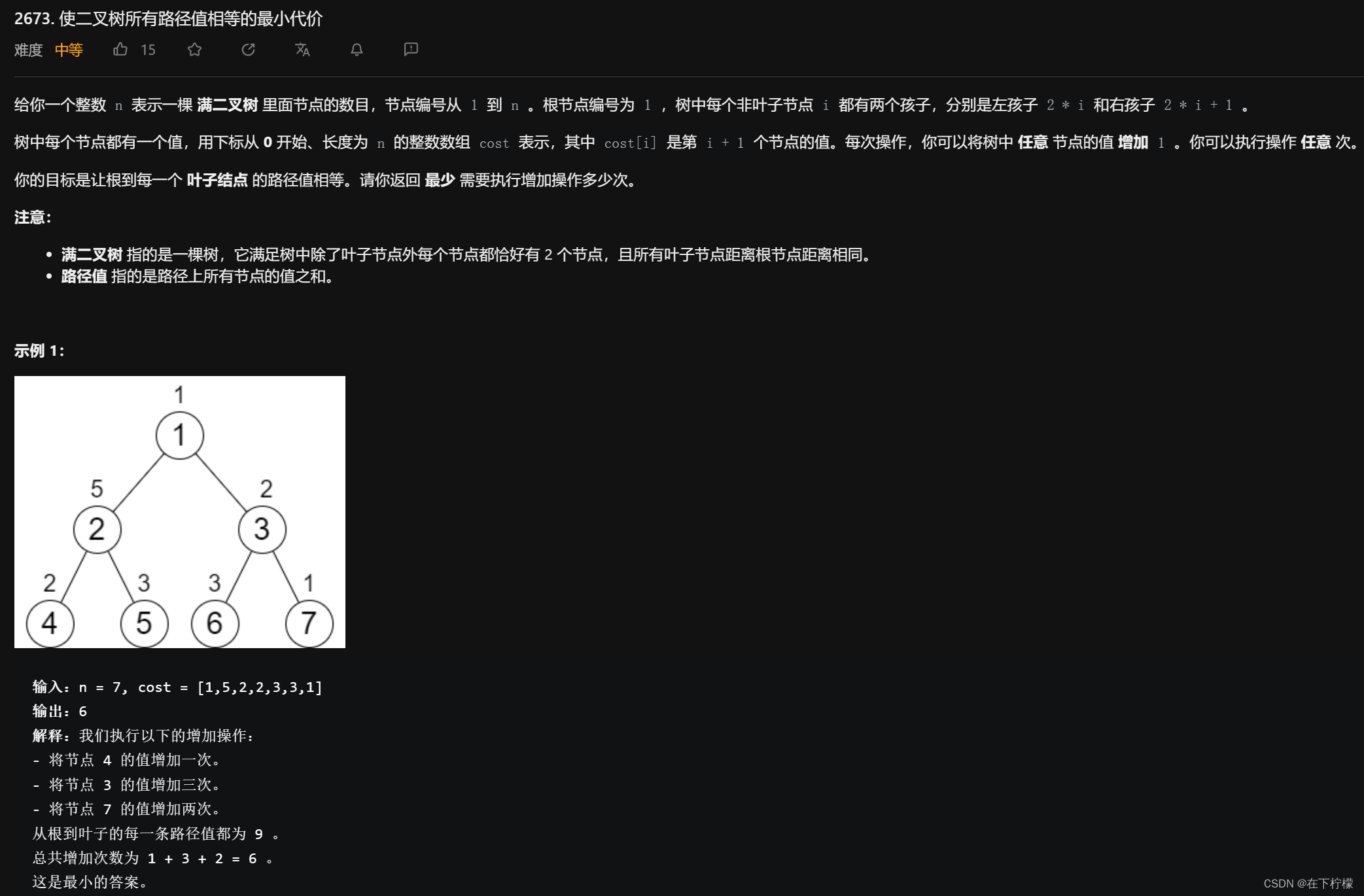
在这里插入图片描述

树中每个非叶子节点 i 都有两个孩子，分别是左孩子 2 * i 和右孩子 2 * i + 1

题目的要求是根节点到每一个叶子结点的路径值之和都相同，如果同一层级的节点值都相同路径和当然相同，但是他要求最少执行次数，这里有两点要注意的：

同一层级节点值要相同，这样同一层级的路径和才有可能相同
改父节点比改子节点需要的操作次数要少

所以自下而上的修改节点值，每层比较的是路径值之和，这里可以先从上到下累加路径和，在自下而上操作的过程中更新其父节点的路径和，示例中的修改顺序是：

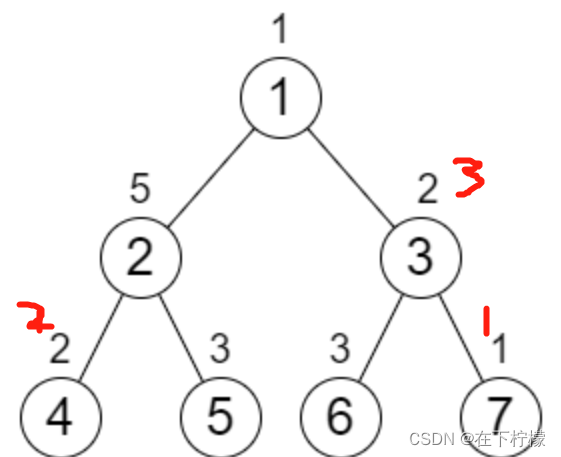
在这里插入图片描述

class Solution:
    def minIncrements(self, n: int, cost: List[int]) -> int:
        for i in range(2, n+1):
            cost[i-1] += cost[i//2-1]
        # print(cost)
        ans = 0
        for i in range(n//2, 0, -1):
            ans += abs(cost[i*2-1] - cost[i*2+1-1])
            cost[i-1] = max(cost[i*2-1], cost[i*2+1-1])
        return ans

5、字符串：记忆化搜索

在这里插入图片描述

记忆化搜索，dfs(i) 是 s 前 i 个字符的答案，最少剩余字符数，每次递归判断选还是不选，不选很简单，直接dfs下一个，剩余字符数加一，选的话需要枚举选哪个

将List转化成Set，可以提高计算效率

class Solution:
    def minExtraChar(self, s: str, dictionary: List[str]) -> int:
        d = set(dictionary)
        n = len(s)
        @cache
        def dfs(i:int) -> int:
            if i<0: return 0
            # 不选这个字符，那剩下字符长度+1
            res = dfs(i-1) + 1
            # 遍历从0到i的字符串，如果s[j:i+1]在列表中，就选这个字符串
            for j in range(i+1):
                if s[j:i+1] in d:
                    res = min(res, dfs(j-1))
            # 选和不选做一个最小值判断，最后返回最小剩余长度值
            return res
        return dfs(n-1)

6、01字符串反转：结论题

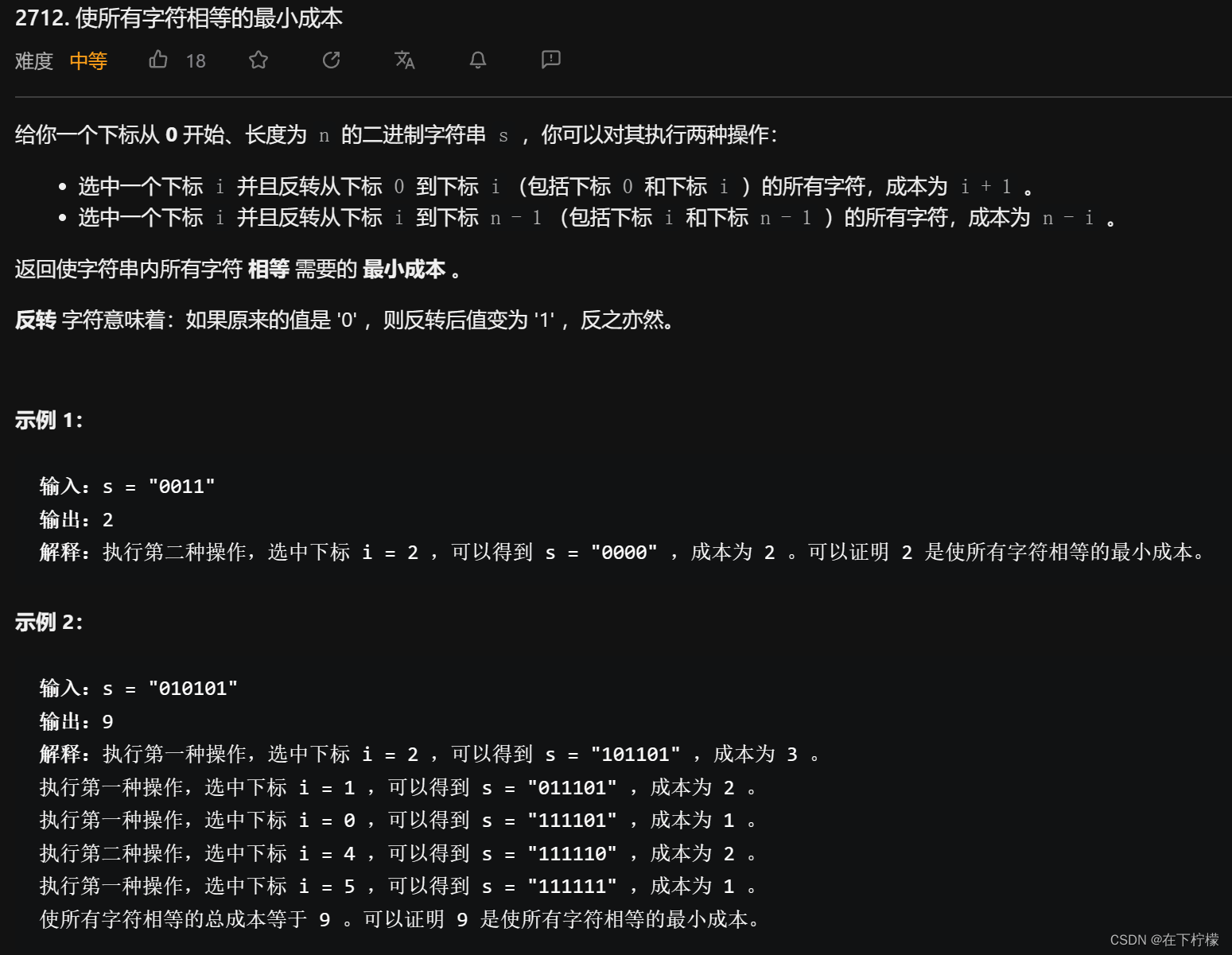
在这里插入图片描述

这道题的难点在于分析例子，示例的解题思路不一定是最好的
010101 -> 110101 -> 000101 -> 111101 -> 111100 -> 111111
0 -> 1 -> 2 -> 3 -> 1 -> 2

可以看到，如果相邻不同字符就反转，反转时判断是左边反转成本小还是右边反转成本小

class Solution:
    def minimumCost(self, s: str) -> int:
        n = len(s)
        ans=0
        for i in range(1,n):
            if s[i]!=s[i-1]:
                ans+=min(i,n-i)
        return ans

7、前缀和：小球碰撞抽象思考

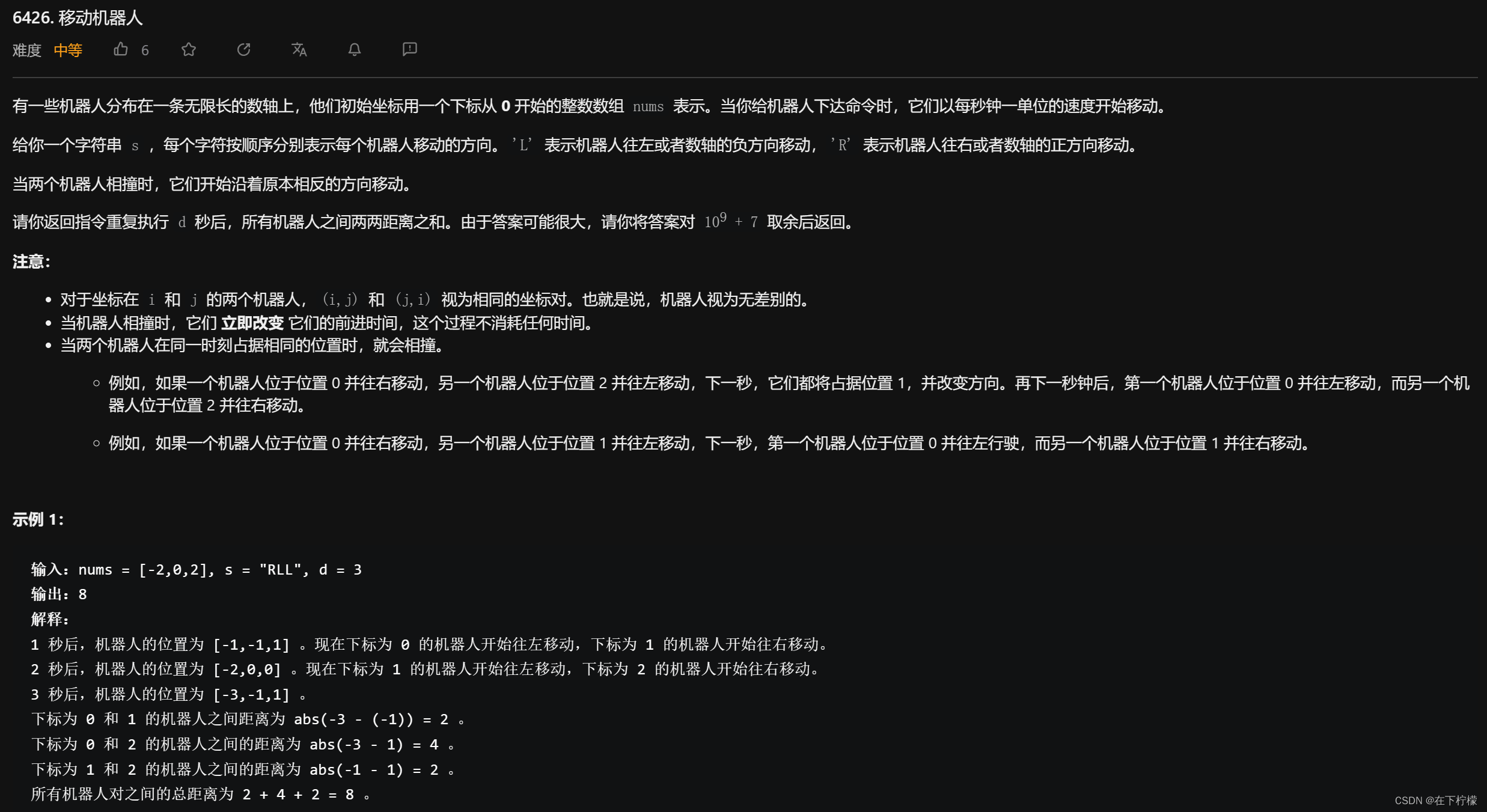
在这里插入图片描述

小球碰撞的结果是反向运动，而我们求的是小球两两之间的距离，那可以看做小球擦肩而过，每个小球按照既定方向运动d个单位长度
求距离时，第 i 个小球和之前小球的距离等于 i*ai 减去前缀和，为了保证符号的一致性，对数组进行排序

class Solution:
    def sumDistance(self, nums: List[int], s: str, d: int) -> int:
        MOD = 10 ** 9 + 7
        n = len(nums)
        # 如果把两个相撞小球抽象成两个相同小球，碰撞之后反向运动和擦肩而过的结果相同
        # 所以题目可以理解为每个小球按照一个方向运动d个单位
        for i in range(n):
            nums[i] += d if s[i]=="R" else -d
        # 排序之后求距离和
        # 第i个和前面的距离和=(ai-a0)+(ai-a1)+...+(ai-ai-1)=i*ai-(a0+...+ai-1)
        # 第i个和前面的距离和=i*nums[i]-s
        nums.sort()
        ans = s = 0
        for i in range(n):
            ans+=i*nums[i]-s
            s+=nums[i]
        return ans % MOD

7、二进制数：逆向思考问题，对结果进行遍历

在这里插入图片描述

这道题第一思路是贪心、递归，但是num2可以小于0，递归判定条件不好确定
所以这道题可以逆向思考，对操作数进行遍历
- 如果操作k次才能使num1==0，则 num1-num2*k 这个数可以分解成k个2**i相加
- 例如示例1，3-(-2)*3 = 9 = 1001 = 1000+1，至少要有两个2**i，即8+1，至多可以有9个1相加，而k==3，正好在 [2, 9] 这个范围内，所以k=3成立

class Solution:
    def makeTheIntegerZero(self, num1: int, num2: int) -> int:
        # 从暴力入手:校举操作次数 k
        # 间题变成:设 x num1 - num2 * k
        #         计算 x 能否分解成 k 个 2
        # k ∈ [x.bit_count(), x]
        for k in range(64):
            x = num1 - num2*k
            if x < k: return -1
            if k >= x.bit_count(): return k

对结果进行遍历，那么这个结果的最大值64是怎么确定的呢？是从数据大小确定的，也可以写个死循环while
x.bit_count()可以返回二进制数中1的个数，比如1001返回2， 1011返回3

8、求质数：list和set的区别

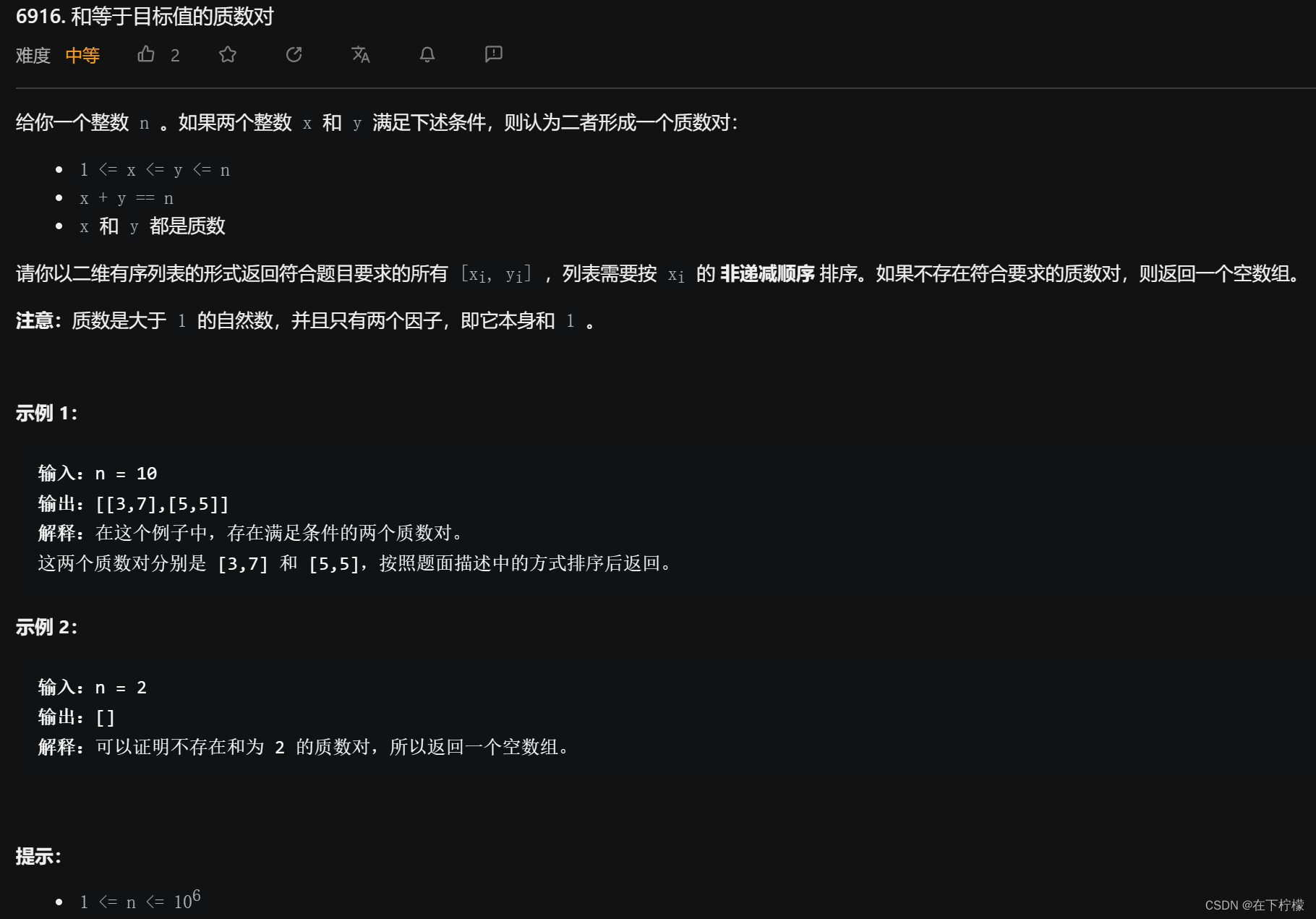
在这里插入图片描述

ma=10**6
def get_primes(M):
    f = [1]*M
    for i in range(2,isqrt(M)+1):
        if f[i]:
            f[i*i:M:i] = [0] * ((M-1-i*i)//i+1)
    return [i for i in range(2,M) if f[i]]

primes = get_primes(ma+1)
vis = set(primes)

class Solution:
    def findPrimePairs(self, n: int) -> List[List[int]]:
        # print(primes)
        # print(vis)
        ans=[]
        for x in primes:
            if x*2>n:
                break
            if (n-x) in vis:
                ans.append([x,n-x])
        return ans

这道题，直接求出数据范围内的所有质数，并把计算过程放在Solution之外，大大减少用时
list和set的区别
- list是有序的，可重复，元素类型可以不一样，通过下标来访问不同位置的元素
  
  常用的一些函数有pop(), append(), extend(), insert()
- set通常是用来进行去重，内容无序不可重复
  
  常用的函数有add(), update(), remove()。同时set的效率要比list高
- 所以遍历时用列表primes，查询是否存在用集合vis
剪枝操作，根据题目要求，当x大于n的一半时就不用继续遍历了，时间优化了17%左右

9、滑动窗口：求子数组个数

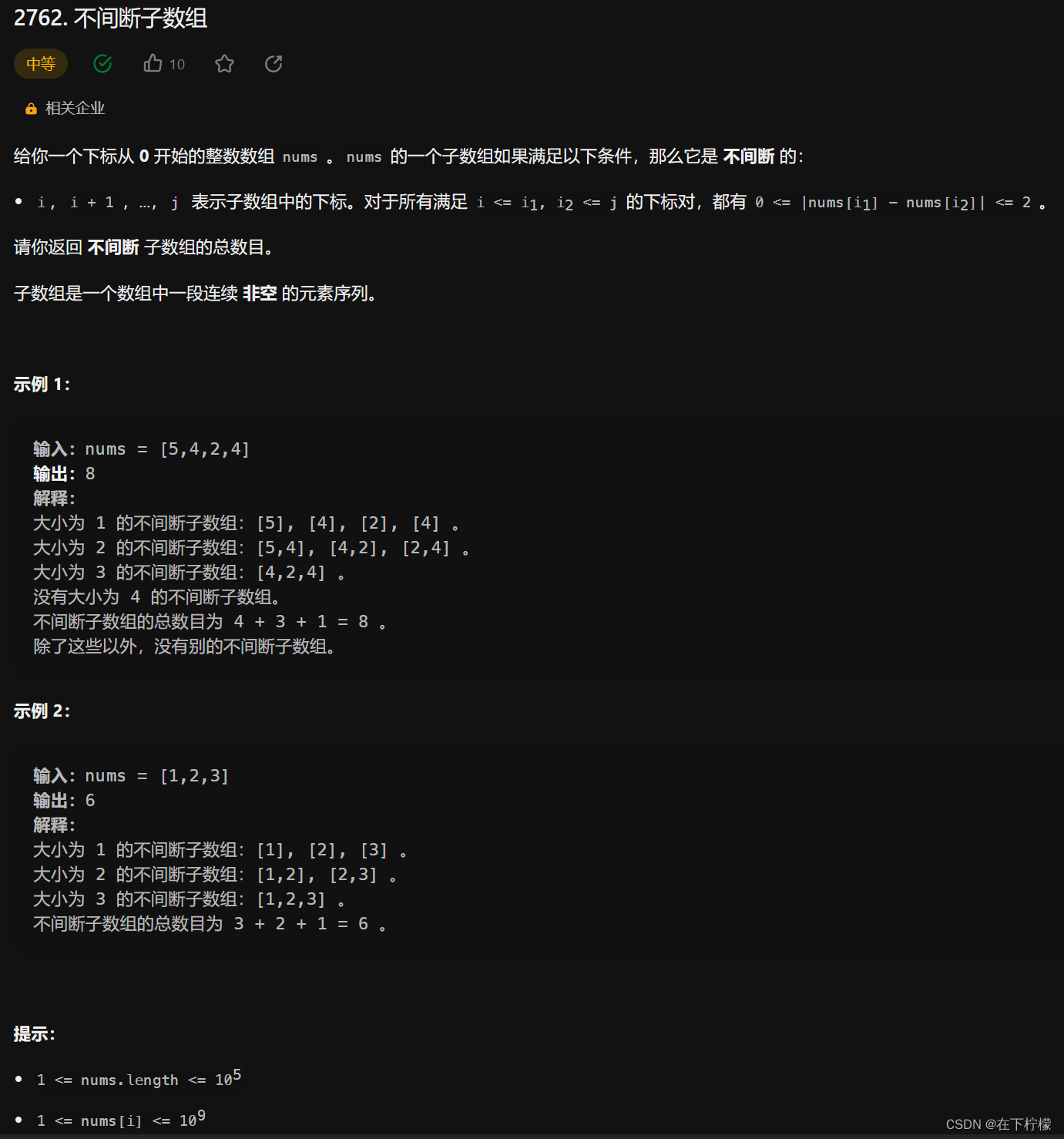
在这里插入图片描述

题目示例的解释迷惑性太强，第一思路是遍历不间断子数组的长度，1…2…3…，直到本轮个数为0截止
数据大小是100000，这种情况需要使用数据结构来优化代码

class Solution:
    def continuousSubarrays(self, nums: List[int]) -> int:
        ans = 0
        left = 0
        cnt = Counter()
        for right, x in enumerate(nums):
            cnt[x] += 1
            while max(cnt)-min(cnt) > 2:
                y = nums[left]
                cnt[y] -= 1
                if cnt[y] == 0:
                    del cnt[y]
                left += 1
            ans += right - left + 1
        return ans

正确思路是遍历数组，遍历到的数字下标为滑动窗口右端点，此时左端点还是上一个子数组的端点，需要根据题目条件不断调整左端点，最后得到的数组为右端点是x的所有符合条件的数组，直接计算所有可能的子数组个数加到ans中即可。
Counter()在python中相当于[int, int]的哈希表
题目示例解释是遍历子数组长度，而正确解法是遍历数组固定右端点，根据题目条件找左端点，然后计算子数组个数，所以以后看题不能盲目相信题解。
滑动窗口在本例中的使用方法是遍历固定右端点，根据题目条件移动确定左端点。

10、最大子数组：DFS+遍历

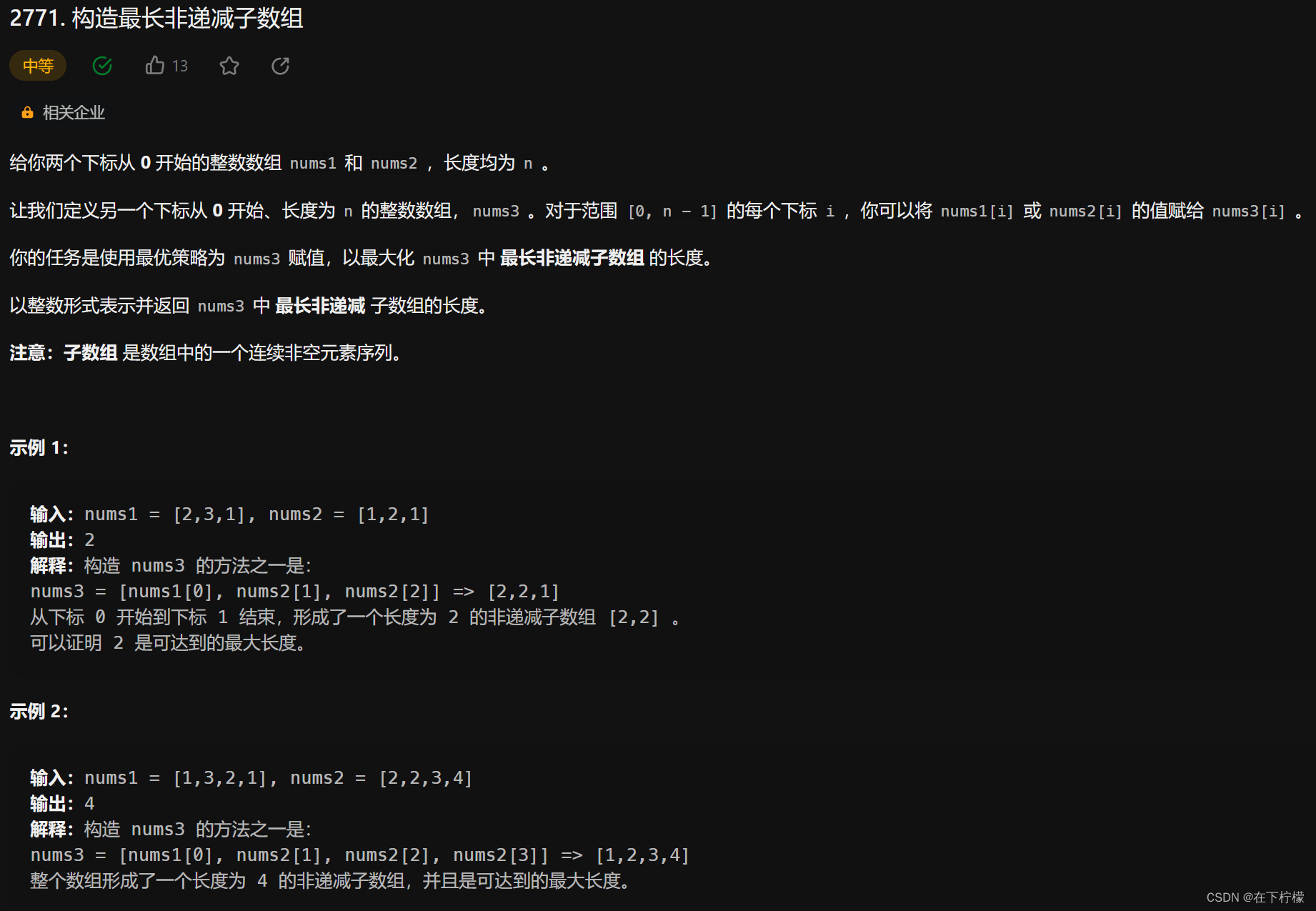
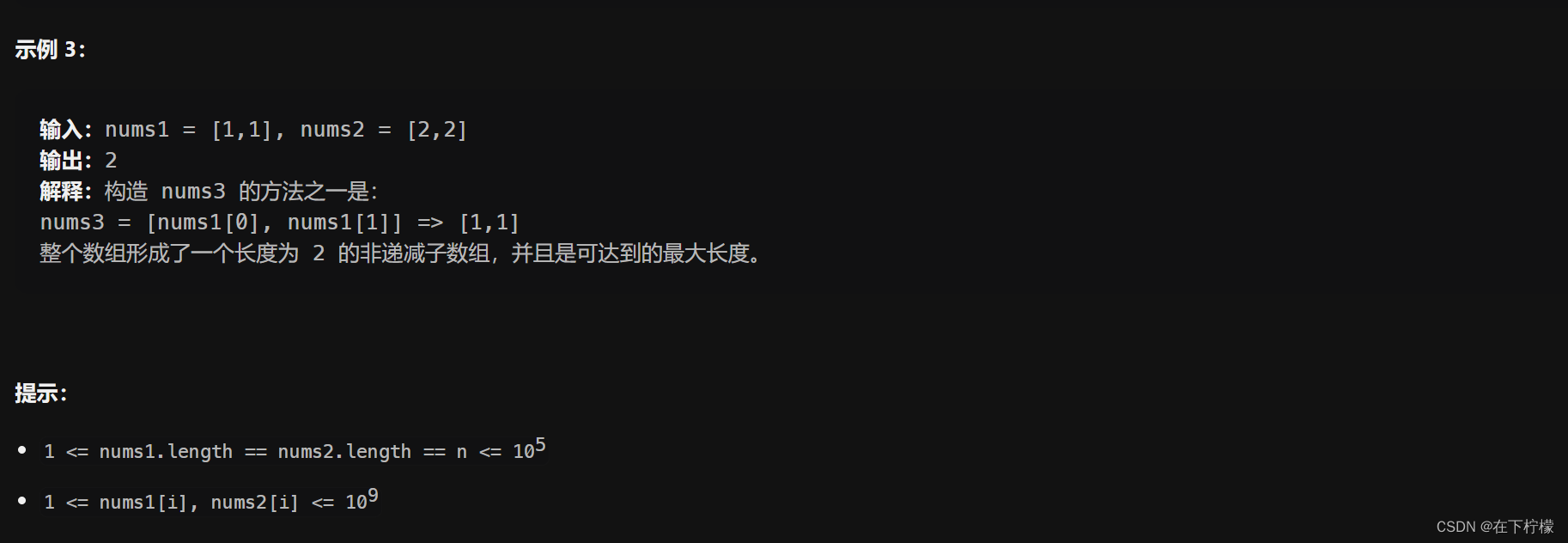
在这里插入图片描述

首先想到dfs，但是很困难，中间可能断节，导致不能返回1，尝试返回1和是否断节的bool，尝试将长度值放在函数参数中，都没有成功

class Solution:
    def maxNonDecreasingLength(self, nums1: List[int], nums2: List[int]) -> int:
        num = (nums1, nums2)
        # dfs(i, 0/1) 表示以 nums1[i]/nums2[i] 结尾的子数组的最大长度
        @cache
        def dfs(i:int, j:int) -> int:
            # 左边没有数字，不需要继续比较了
            if i == 0: return 1
            res = 1
            if nums1[i-1] <= num[j][i]:
                res = max(res, dfs(i-1, 0) + 1)
            if nums2[i-1] <= num[j][i]:
                res = max(res, dfs(i-1, 1) + 1)
            return res
        n = len(nums1)
        ans = 0
        for i in range(n):
            ans = max(ans, dfs(i, 0), dfs(i, 1))
        return ans

我的思路有问题，不应该将dfs函数的参数和返回值上下功夫，这里的答案，dfs表示以初始化数字结尾的子数组的最大长度，这样就不用考虑断节问题了，直接遍历一遍，就可以找到最大长度
这里有一个小技巧，将两个数组组合成tuple，就可以传下标，然后用nums[j][i]表示任意数组

11、字符串和字符串数组：遍历查找技巧

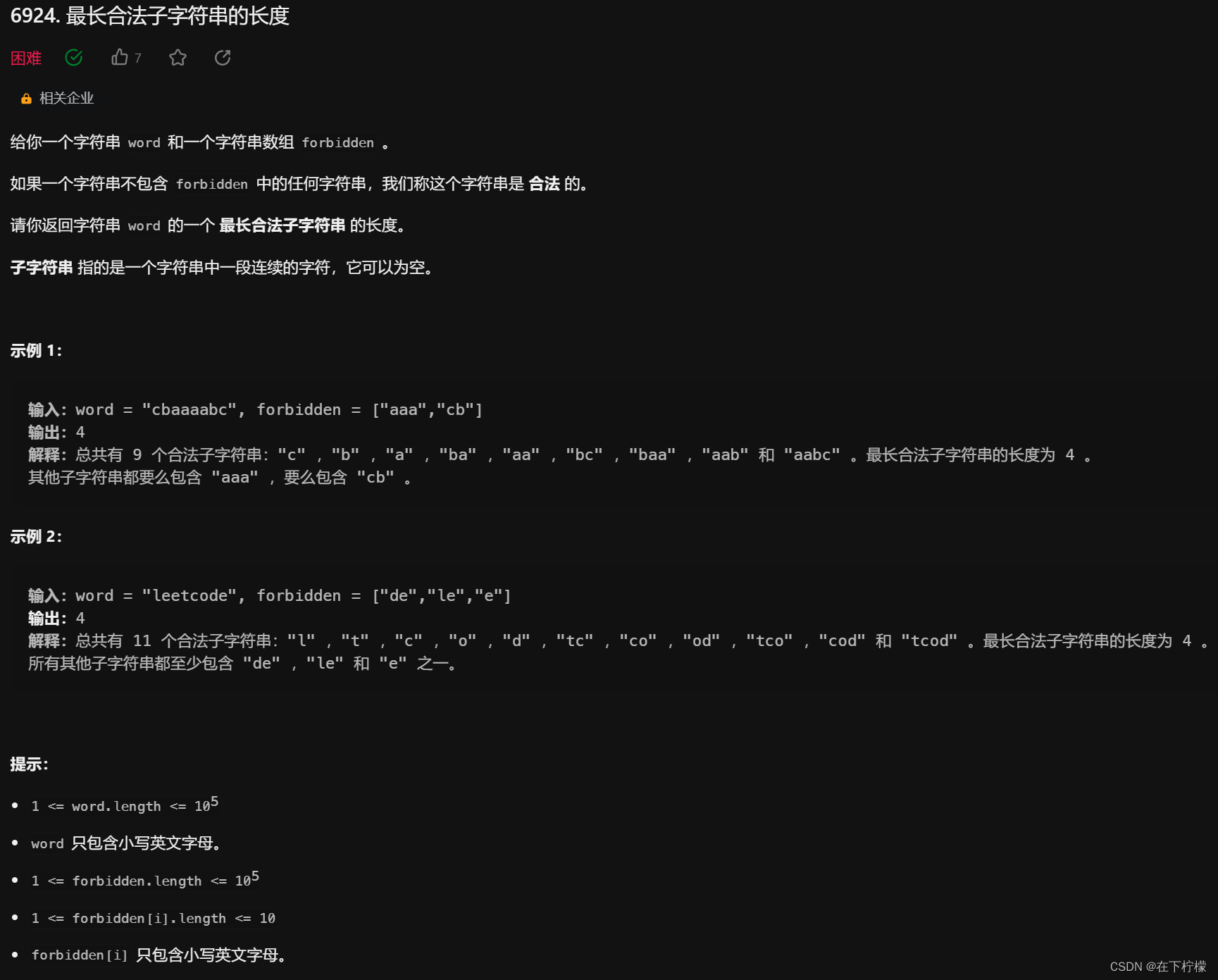
在这里插入图片描述

最初的想法是遍历左端点，移动右端点，寻找以左端点为首的字符串的最大长度，但是预想到会超时
看到数据大小，length最大只有10，这是明显的遍历暗示
遍历右端点，移动左端点，每次枚举字符串，如果在左右端点之中的话就移动左端点，由于出现字符串只会是新加入的右端字符导致的，所以从右边开始枚举，而且最多只需要枚举10次，因为length最大只有10

class Solution:
    def longestValidSubstring(self, word: str, forbidden: List[str]) -> int:
        res = 0
        s = set(forbidden) # 查找速度快
        l = 0 # 遍历右端点，移动左端点
        for r in range(len(word)):
            for i in range(r, max(r-10, l-1), -1): # 从后往前找，forbidden最长为10
                if word[i:r+1] in s:
                    l = i+1
                    break
            res = max(res, r-l+1)
        return res

技巧题，解题思路很简单，但是实现需要一些技巧

go

1、01背包，快速幂计算

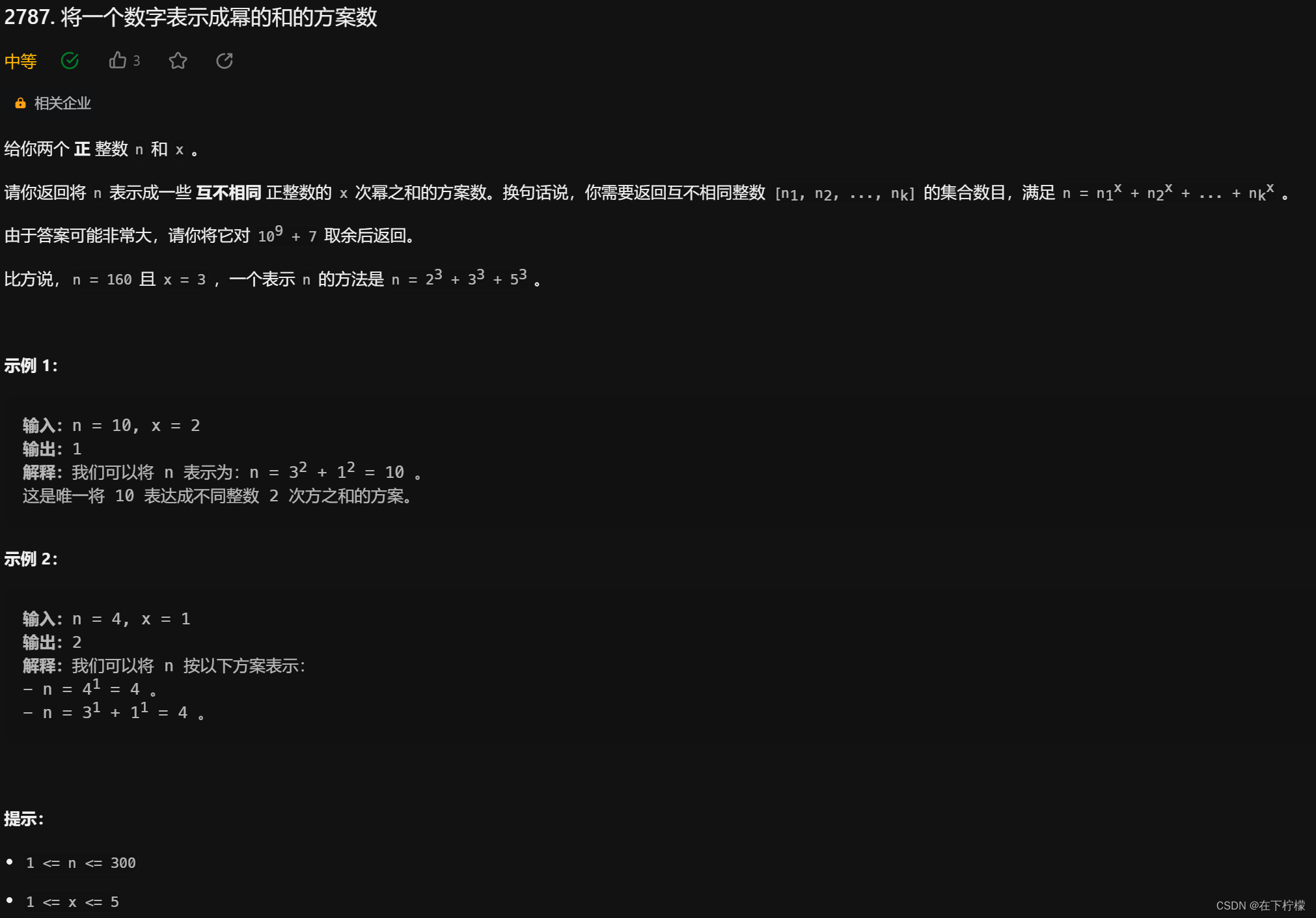
在这里插入图片描述

经典01背包问题，背包容量是n，从1-n中挑选任意个数字，每个数字的权重是i**x，问有几种方案

func numberOfWays(n int, x int) int {
	f := make([]int, n+1)
	f[0] = 1
	for i := 1; pow(i, x) <= n; i += 1 {
		v := pow(i, x)
		for s := n; s >= v; s-- {
			f[s] += f[s-v]
		}
	}
	return f[n] % (1e9 + 7)
}
func pow(x, n int) int {
	res := 1
	for ; n > 0; n /= 2 {
		if n%2 > 0 {
			res *= x
		}
		x *= x
	}
	return res
}

创建一个n+1的数组，这样下标就是选择是数字，数组中的值就是这个数字符合条件的组合数，如果更大的数字挑选这个数字作组合的话，组合数就是这个数字在数组中的值。
对权重值小于n的数字进行遍历，并更新对于数字n，符合条件的组合数，注意不仅要更新n，还要更新之前的数字，否则后续计算失效
快速计算幂，每次指数折半，将底数翻倍，如果本轮指数是奇数，就将底数乘到res中

2、字符串组合

在这里插入图片描述

这道题猛地一看没有什么思路，这时候可以尝试暴力，直接遍历abc所有排列，尝试合并成一个字符串，每种结果相互比较，选出最短且字典序最小的结果

func minimumString(a string, b string, c string) string {
    // 合并s和t，将t插入s后面
    f := func(s string,t string) string{
        if strings.Contains(s,t){
            return s
        }
        if strings.Contains(t,s){
            return t
        }
        n := len(s)
        start := min(n,len(t))
        for i:=start;i>=0;i--{
            if s[n-i:]==t[:i]{
                return s+t[i:]
            }
        }
        return s+t
    }
    
    ans := ""
    ss := []string{a,b,c}
    turn := [][]int{{0,1,2},{0,2,1},{1,0,2},{1,2,0},{2,0,1},{2,1,0}}
    for _,nums := range turn{
        res := f(f(ss[nums[0]],ss[nums[1]]),ss[nums[2]])
        // fmt.Println(res)
        if ans=="" || len(ans)>len(res) || len(ans)==len(res) && ans>res{
            ans=res
        }
    }
    return ans
}
func min(a int,b int)int{
    if a>=b{
        return b
    }else{
        return a
    }
}

合并的函数中，比较s的后缀和t的前缀，在调用时需要使用全排列，即turn二维数组，最终结果比较长度，如果一样长比较字典序，注意go中两个字符串比较字典序可以直接比较
这里需要使用全排列，因为在合并函数中每次返回的是最小的结果，但是两次合并贪心最优不代表最终结果最优，可能会出现这种情况

"gfaa" + "aaccf" + "faaacc"
如果不适用全排列，两次贪心的结果是 >> "gfaaccfaaacc"
但是全排列就考虑到021这种情况，结果是 >> "gfaaaccf"

所以我们采用全排列+贪心的方法来避免每次最短结果不是最短这种尴尬情况

3、数位dp，模拟记忆化搜索，位运算

在这里插入图片描述

对每一位数进行递归，遍历所有可能出现的情况，每一位数的取值范围该如何确定？
最小值：如果全是0，那么有可能出现010这种情况，10明显是符合条件的，但是数字0出现了两次，所以应该把0出现的情况划分开。如果前面所有位数都没有选值，那么这一位也可以不选，即为跳过，也可以选，可以选的最小值是1，如果前面有一位已经选了>0的值，后面就不能跳过了，此时可以选的最小值是0
最大值：如果前面的位数都选了最大的值，比如135 >> 13*，那么这一位最大可以选5，如果前面的位数有一个没有定格选，那么这一位最大可以选9
对上面两种情况需要维护两个bool值，isLimit表示这一位是否被限制不能选9，isNum表示前面是否选了数字
流程确定，每次先判断能不能跳过，然后从最小值到最大值遍历，如果数字还没被选，那么符合题目条件，这里我们用位运算来记录前面选了哪些数
最后使用记忆化数组来提高计算效率，分别用第i位和位运算来当下标，由于两个bool值的存在，我们选择记录!isLimit && isNum这种情况，因为这种情况最多

func countSpecialNumbers(n int) int {
    s := strconv.Itoa(n)
    m := len(s)
    // dp数组，模拟记忆化搜索，只记录!isLimit && isNum的情况，其他情况不能合并并且发生次数少
    cache := make([][1<<10]int, m)
    for i := range cache{
        for j := range cache[i]{
            cache[i][j] = -1
        }
    }
    // 第i位填数字，前i位选过的数字记录在mask中
    // isLimit表示，如果前i位全是n[i]，那么这一位最多填n[i]
    // isNum表示，如果前i位选过数字，那么这一位只能选数字，不能跳过
    var f func(int, int64, bool, bool) int
    f = func(i int,mask int64,isLimit bool,isNum bool) int{
        if i==m{
            if isNum{
                return 1
            }else{
                return 0
            }
        }

        res := 0
        // 先检查cache是否已经记录本次递归，如果是直接返回结果，最终记录结果
        if !isLimit && isNum{
            p := &cache[i][mask]
            if *p>=0{
                return *p
            }
            defer func(){*p = res}()
        }

        // 跳过
        if !isNum{
            res += f(i+1,mask,false,false)
        }

        // 不跳过
        start := 1
        if isNum{
            start = 0
        }
        end := 9
        if isLimit{
            end = int(s[i]-'0')
        }
        for j:=start;j<=end;j++{
            if mask>>j & 1 == 0 {
                res += f(i+1,mask|(1<<j),isLimit && j==end,true)
            }
        }
        return res
    }
    return f(0,0,true,false)
}

4、多源BFS，并查集

在这里插入图片描述

首先找到全部的1，然后从1开始扩散，记录数组中所有点离最近的1的距离，从距离最大的几个点扩散，更新并查集，并判断从左上是否联通右下，如果是就返回，如果不是就遍历下一个距离的点集，最终返回0
为什么用多源BFS：所有的1以相同速度同时扩散，就可以判断出某个点离哪个1最近
为什么用并查集：可以快速判断两个点是否联通

func maximumSafenessFactor(grid [][]int) int {
    n := len(grid)
    // 查找 1 的下标
    type pair struct{ x, y int}
    q := []pair{}
    dist := make([][]int, n)
    for i, row := range grid{
        dist[i] = make([]int, n)
        for j, x := range row{
            if x==1{
                q = append(q, pair{i, j})
            }else{
                dist[i][j] = -1
            }
        }
    }
    // fmt.Println(q,dist)

    // 从1开始扩散，记录到1的距离，根据距离分层，记录下标
    // 由于有多个1，所以用多源BFS，滚动数组遍历grid，来更新距离，保存下标
    dir4 := []pair{{-1,0}, {1,0}, {0,-1}, {0,1}}
    groups := [][]pair{q}
    for len(q) > 0{
        temp := q
        q = nil
        for _,p := range temp{
            for _,d := range dir4{
                x, y := p.x+d.x, p.y+d.y
                if 0<=x && x<n && 0<=y && y<n && dist[x][y]<0{
                    q = append(q,pair{x,y})
                    dist[x][y] = len(groups)
                }
            }
        }
        groups = append(groups,q)
    }
    // fmt.Println(groups,dist)

    // 由层数从大到小遍历，对每个点遍历上下左右，只可以去层数更大的点
    // 如果当前层数遍历完成后左上能到右下，就返回层数，判断左上右下两点是否联通使用并查集
    fa := make([]int, n*n)
    for i := range fa{
        fa[i] = i
    }
    var find func(int)int
    find = func(x int)int{
        if fa[x] != x{
            fa[x] = find(fa[x])
        }
        return fa[x]
    }

    for ans := len(groups)-2; ans>0; ans-=1{
        for _,p := range groups[ans]{
            i, j := p.x, p.y
            for _,d := range dir4{
                x, y := p.x+d.x, p.y+d.y
                if 0<=x && x<n && 0<=y && y<n && dist[x][y] >= dist[i][j]{
                    fa[find(x*n+y)] = find(i*n+j)
                }
            }
        }
        if find(0) == find(n*n-1){
            // fmt.Println(fa)
            return ans
        }
    }
    return 0
}

输出示例：

在这里插入图片描述

// 所有的1
[{0 3} {3 0}] 
// 距离记录前的样子
[[-1 -1 -1 0]
 [-1 -1 -1 -1]
 [-1 -1 -1 -1]
 [0 -1 -1 -1]]
// 距离更新后的样子
[[3 2 1 0]
 [2 3 2 1]
 [1 2 3 2]
 [0 1 2 3]]
// 根据层数来分组的点
[[{0 3} {3 0}] 
 [{1 3} {0 2} {2 0} {3 1}]
 [{2 3} {1 2} {0 1} {1 0} {2 1} {3 2}]
 [{3 3} {2 2} {1 1} {0 0}]
 []] 
// 并查集维护的数组
[14 14 2 3 14 4 9 7 8 14 9 14 12 13 14 14]

5、有序队列

在这里插入图片描述

双指针遍历数组，下标间距正好是x，前一个指针添加到一个有序队列中，后一个指针在有序队列中查找与之相近的值，最后返回结果
力扣中支持第三方库github.com/emirpasic/gods/tree/v1.18.1，提供了一个红黑树，插入数据后直接根据key值大小排列成一个有序数组，我们将key设为nums[i]，value设为空

func minAbsoluteDifference(nums []int, x int) int {
    ans := math.MaxInt
    // 第三方库，把红黑树当做有序队列
    tree := redblacktree.NewWithIntComparator()
    // 只用排序功能，只需要设置key值，
    // 首先插入两个哨兵，分别位于有序队列的头和尾，保证每次查找都能返回一个结果
    tree.Put(math.MaxInt, nil)
    tree.Put(math.MinInt/2, nil)
    // 双指针遍历数组，把前一个数添加到队列中，后一个数在队列中查找刚好大于和小于的叶子节点
    for i,y := range nums[x:]{
        tree.Put(nums[i], nil)
        c,_ := tree.Ceiling(y)
        f,_ := tree.Floor(y)
        ans = min(ans, min(y-f.Key.(int), c.Key.(int)-y))
    }
    return ans
}
func min(i,j int)int{if i<j{return i}else{return j}}

6、线性dp

在这里插入图片描述

第一眼思路是dfs，维护房屋end和买家下标，每次判断要不要卖给买家，但是超时了，使用dp数据优化，但是数据范围过大，不能生成 [1e5] [1e5] int 大小数组
正确解法是线性dp，递推式dp[n] = max( dp[n-1], max( dp[starti]) + goldi )

// DP问题两个思路，
// 一个是选或不选，是否卖当前房子，
// 一个是枚举选哪个，以当前房子结尾最多可以赚多少钱
func maximizeTheProfit(n int, offers [][]int) int {
    // 线性dp，选或不选，不选f[n+1]=f[n]，选，枚举选哪个f[n+1]=max(f[starti]+goldi)
    groups := make([][][2]int, n)
    for _,arr := range offers{
        groups[arr[1]] = append(groups[arr[1]], [2]int{arr[0], arr[2]})
    }
    dp := make([]int, n+1)
    // 从递推式可知，计算n+1需要用到f[start]，所以从前往后遍历
    for i:=1;i<=n;i+=1{
        // 不选
        dp[i] = dp[i-1]
        // 选，枚举选哪个
        for _,arr := range groups[i-1]{
            dp[i] = max(dp[i], dp[arr[0]]+arr[1])
        }
    }
    return dp[n]
}
func max(i,j int)int{if i>=j{return i}else{return j}}

这道题我的问题在于过度依赖dfs和dp数组优化，对于dp问题，应该从选或不选入手，选则继续考虑枚举选哪个

7、对数组至多删除k个元素，求子数组最大值

在这里插入图片描述

这道题就是没思路，总不能对每个元素进行遍历，每次操作之后求一次子数组长度
当直接对数组遍历不行时，就需要对数组进行预处理，以每个元素分组，记录同一类元素下标，遍历下标数组，维护一个最大值
例如nums = [1,3,2,3,1,3], k = 3，元素分组后的结果是[[] [0 4] [2] [1 3 5] [] [] []]，如何遍历才能考虑全所有情况，找到最大的数组长度呢？答案是使用双指针，遍历右端点，移动左端点，寻找以当前右端点结尾数组满足题目要求的左端点。

//对nums进行预处理，根据值对下标分组
//对每组进行双指针遍历，寻找满足要求的子数组，维护最大长度
func longestEqualSubarray(nums []int, k int) int {
    //数据范围 0<nums[i]<n，所以不用map，直接用[][]int
    n := len(nums)
    pos := make([][]int, n+1)
    for i,x := range nums{
        pos[x] = append(pos[x], i)
    }
    fmt.Println(pos)
    //对每一组进行遍历，维护子数组最大值
    ans := 0
    for _,arr := range pos{
        //如何遍历才能考虑全所有情况？我们只需要找数组最长的情况，所以使用双指针遍历
        //遍历右端点，移动左端点，使得中间删除元素刚好小于k，这个长度就是这个右端点的长度
        l := 0
        for r,idx := range arr{
            //删除次数=下标数组记录的nums长度-下标数组arr的长度
            //       =一共有几个数字-不需要删除的数字
            for (idx-arr[l]+1) - (r-l+1) > k{
                l += 1
            }
            ans = max(ans,r-l+1)
        }
    }
    return ans
}
func max(i,j int)int{if i>=j{return i}else{return j}}

这道题是个套路题，对数组操作，并求满足题目要求值，这是一个出题模板

8、前缀和

数组问题一个通用有效方法是计算前缀和、前缀最大值、后缀最大值等等

在这里插入图片描述

数组预处理，整除为1，否则为0，双指针遍历数组，查找子数组中满足1数量的所有子数组
查找子数组数量这一步不好做，可以使用前缀数组的方法，

func countInterestingSubarrays(nums []int, m int, k int) int64 {
    // 如果能除尽，算作1，否则为0，为了得到数量，还需要求前缀和，用p[r]-p[l]来表示[l, r]中的这个数量
    pre := make([]int, len(nums)+1)
    for i,x := range nums{
        pre[i+1] = pre[i]
        if x%m == k{
            pre[i+1]+=1
        }
    }
    fmt.Println(pre)
    // 求 (p[r] - p[l]) % m == k
    // => (p[r] - p[l] + m) % m == k % m 
    // => (p[r] - k + m) % m == p[l] % m
    // 有多少个上式成立，就可以往ans中加几个值，
    // 遍历前缀数组，使用哈希表查询以当前值为right，记录以当前值为left
    ans := 0
    cnt := map[int]int{}
	for _, v := range pre {
        ans += cnt[(v - k + m) % m]
        cnt[v%m]+=1
    }
    return int64(ans)
}

[3,1,9,6] => [0 1 1 2 3] => 2

9、矩阵处理，全排列

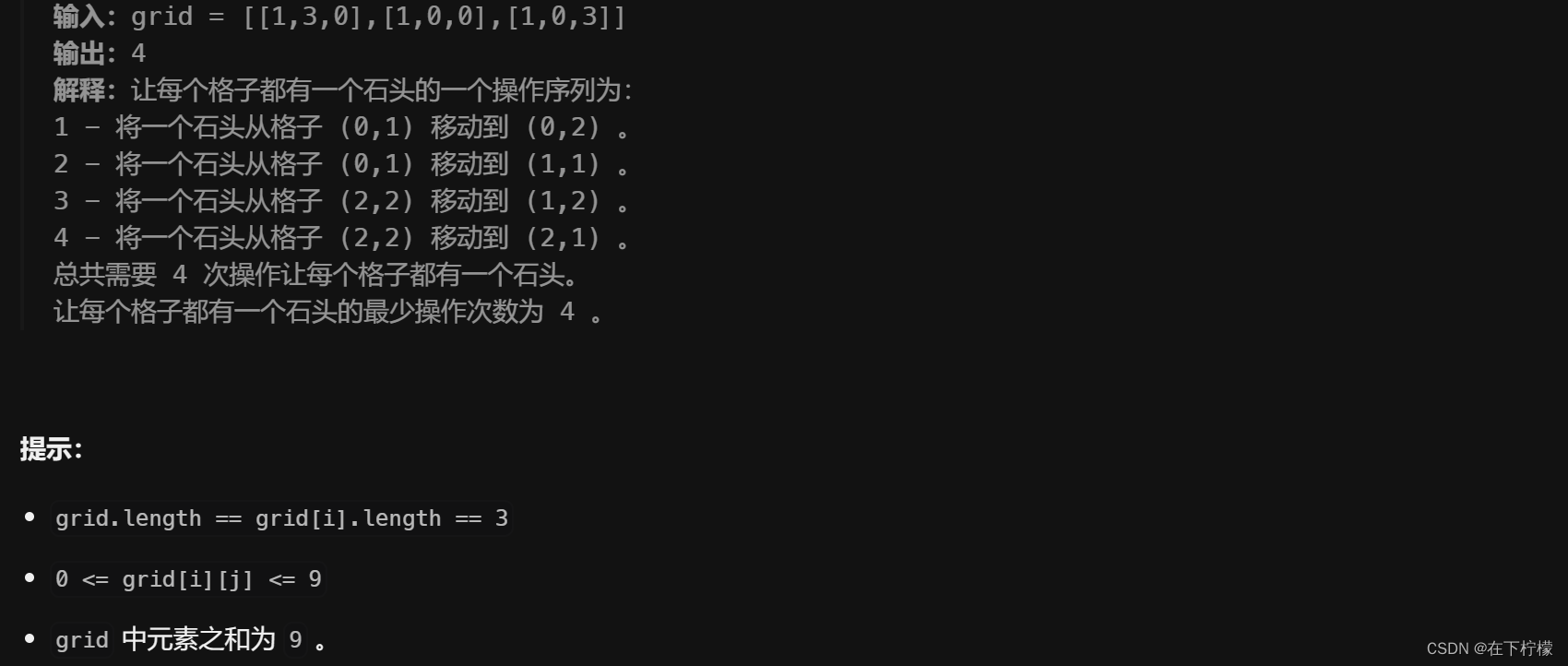
在这里插入图片描述

这个题最初打算先对矩阵预处理，分别记录石头多的和缺石头的，然后缺石头的从距离最近处取石头
还有另外一种解法，首先预处理，石头多的，多几次就记录几次，如下
- [[0 1] [0 1] [2 2] [2 2]] : [[0 2] [1 1] [1 2] [2 1]]
然后求石头多的全排列，分别和缺石头的对应，计算距离，如此难点就成了计算全排列

func minimumMoves(grid [][]int) int {
    from := make([][]int, 0)
    to := make([][]int, 0)
    for i,arr := range grid{
        for j,x := range arr{
            if x>1{
                for c:=1; c<x; c+=1{
                    from = append(from, []int{i,j})
                }
            }else if x==0{
                to = append(to, []int{i,j})
            }
        }
    }
    fmt.Println(from," : ",to)
    // 枚举from的全排列，分别计算与to的移动次数
    ans := math.MaxInt
    permute(from, 0, func(){
        temp := 0
        for i,f := range from{
            temp += abs(f[0] - to[i][0]) + abs(f[1] - to[i][1])
        }
        ans = min(ans, temp)
    })
    return ans
}
func permute(arr [][]int, idx int, do func()){
    if idx==len(arr){
        do()
        return
    }
    permute(arr, idx+1, do)
    for j:=idx+1;j<len(arr);j+=1{
        arr[idx], arr[j] = arr[j], arr[idx]
        permute(arr, idx+1, do)
        arr[idx], arr[j] = arr[j], arr[idx]
    }
}
func abs(x int) int { if x < 0 { return -x }; return x }
func min(a, b int) int { if b < a { return b }; return a }

在全排列函数permute中，分别求首元素固定和首元素移动的情况

10、前缀最大值、后缀最大值

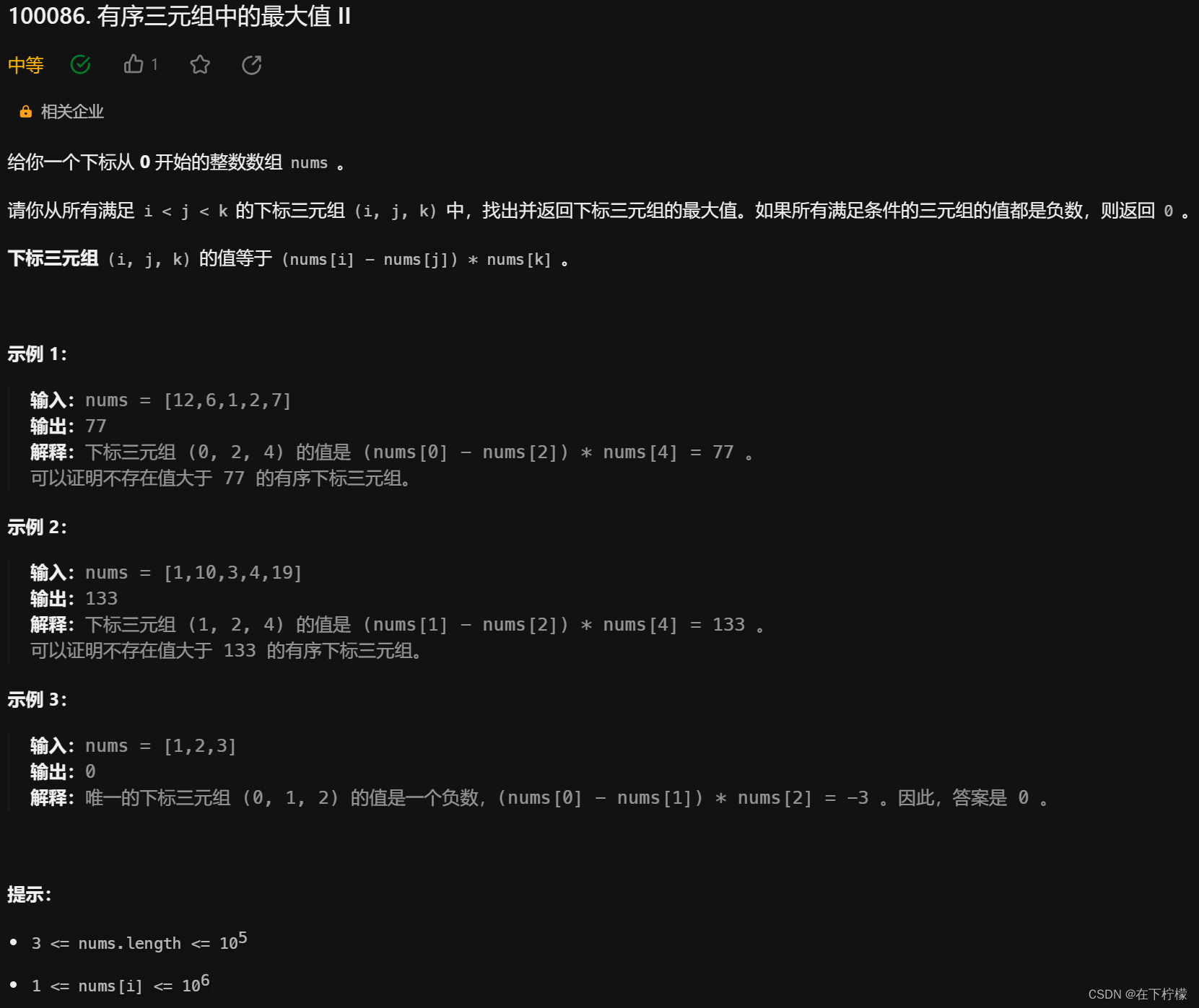
在这里插入图片描述

这道题我想复杂了，我想的是遍历找到最小的j，然后分别求两边最大的i和k，k使用map，i使用max
实际上直接遍历j，两边的最大值分别用数组的前缀最大值和后缀最大值来计算
还有一种一次遍历的方法，遍历k，同时维护max(nums[i]-nums[j])，以及max(nums[i])

方法一：

func maximumTripletValue(nums []int) int64 {
    // 分别计算前缀最大值和后缀最大值
    n := len(nums)
    pre := make([]int,n)
    pre[0] = nums[0]
    suf := make([]int,n)
    suf[n-1] = nums[n-1]
    for i:=0;i<n-1;i+=1{
        pre[i+1] = max(pre[i],nums[i+1])
    }
    for i:=n-1;i>0;i-=1{
        suf[i-1] = max(suf[i], nums[i-1])
    }
    // fmt.Println(pre, suf)
    res := 0
    for i,x := range nums[1:n-1]{
        res = max(res, (pre[i]-x)*suf[i+2])
    }
    return int64(res)
}
func max(i,j int)int{if i>=j{return i}else{return j}}

方法二：

func maximumTripletValue(nums []int) int64 {
    res := 0
    // 遍历k，维护一个max_diff，res=max_diff*nums[k]，而max_diff=max_pre-nums[k]
    max_diff := 0
    max_pre := 0
    for _,x := range nums{
        // 把k当做k
        res = max(res, max_diff*x)
        // 把k当做j
        max_diff = max(max_diff, max_pre-x)
        // 把k当做i
        max_pre = max(max_pre, x)
    }
    return int64(res)
}
func max(i,j int)int{if i>=j{return i}else{return j}}