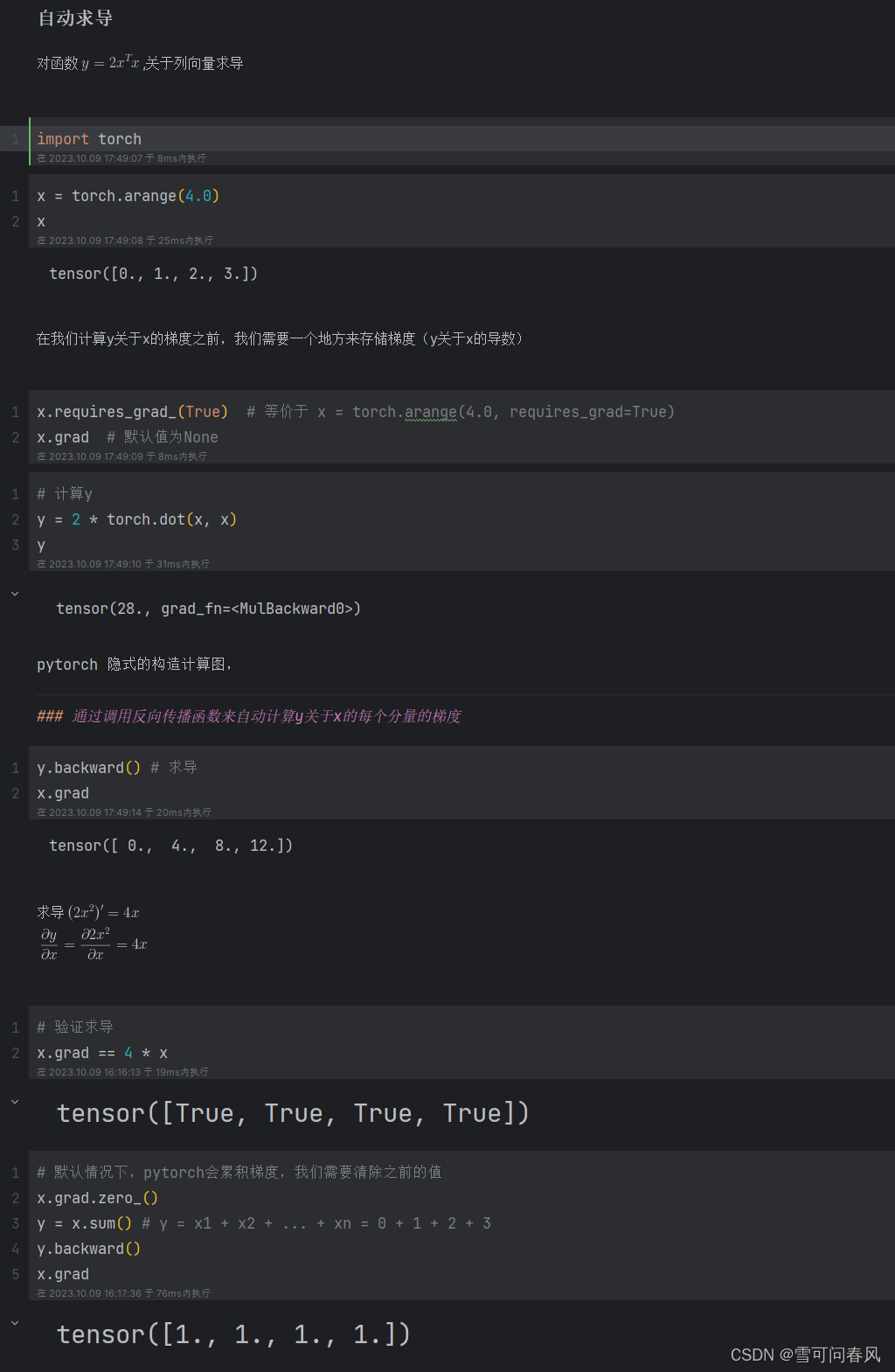
一、题目描述与要求

在二叉树中找到两个节点的最近公共祖先_牛客题霸_牛客网 (nowcoder.com)

题目描述

给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2，请找到 o1 和 o2 的最近公共祖先节点。

数据范围：树上节点数满足1≤n≤10的5次方  , 节点值val满足区间 [0,n)

要求：时间复杂度O(n)

注：本题保证二叉树中每个节点的val值均不相同。

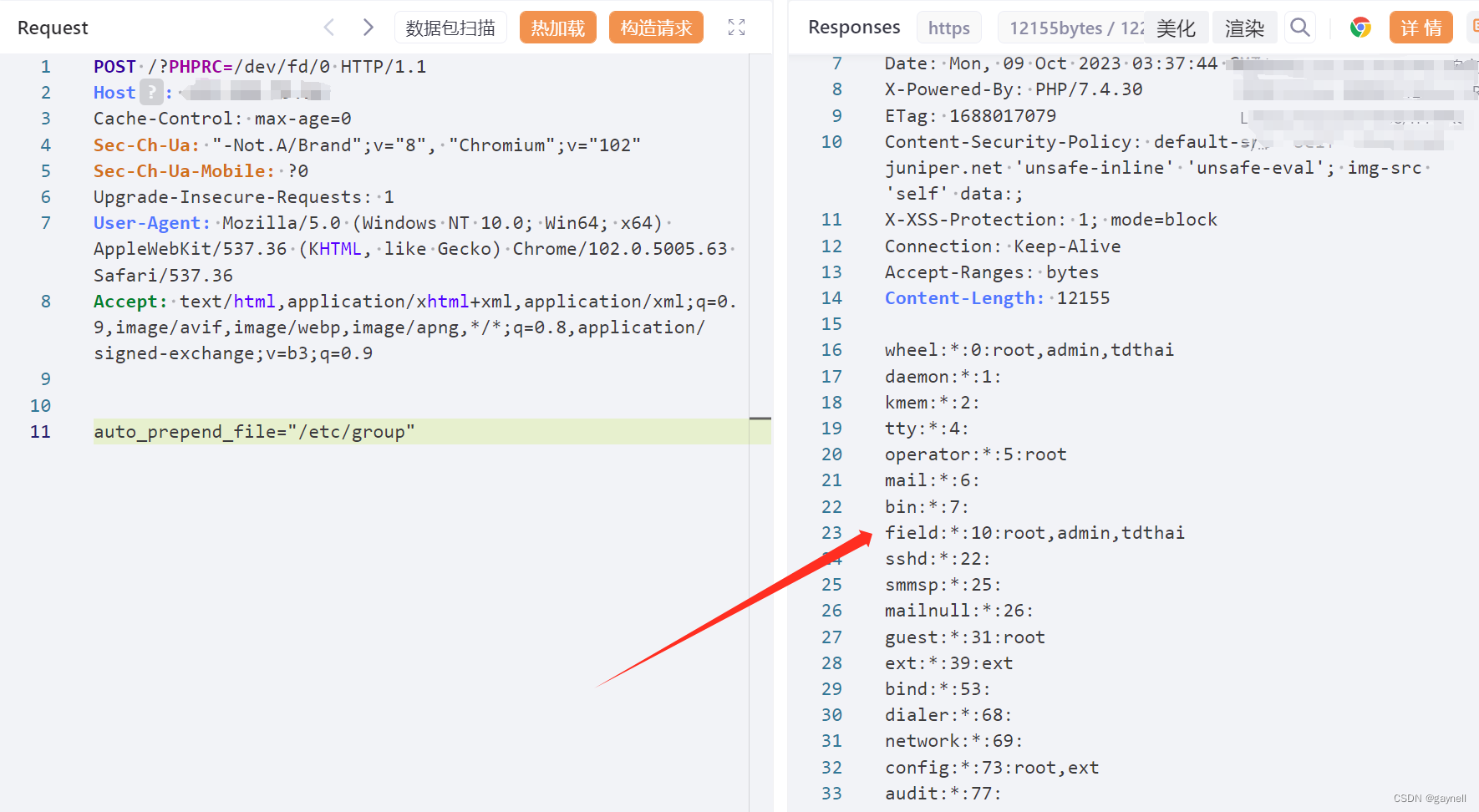
如当输入{3,5,1,6,2,0,8,#,#,7,4},5,1时，二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示：

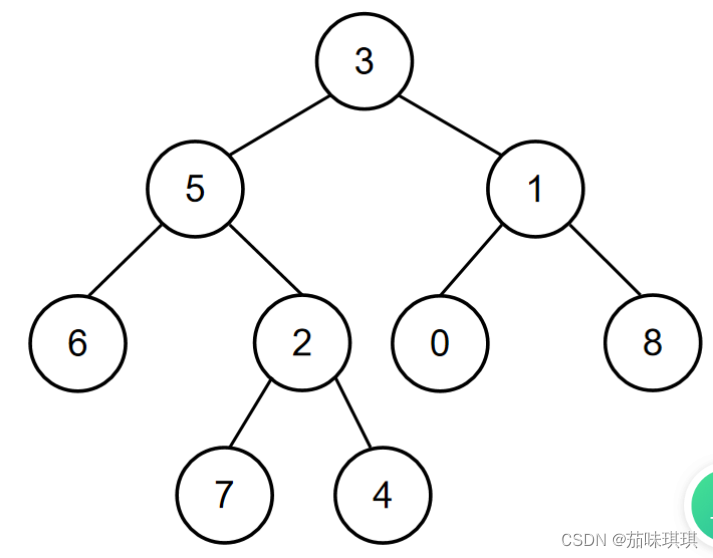
所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3，所以对应的输出为3。

节点本身可以视为自己的祖先

示例

示例1：

输入：{3,5,1,6,2,0,8,#,#,7,4},5,1

返回值：3

示例2：

输入：{3,5,1,6,2,0,8,#,#,7,4},2,7

返回值：2

---

二、解题思路

根据题目要求，我们需要找到二叉树中两个节点的最近公共祖先，与二叉搜索树不同的是二叉树中节点的排序是没有规律的，所以如果我们按照二叉搜索树的思路去解决这道题目的话，需要改变寻找路径的方法

对于二叉树我们想要找到从根节点到一个结点的路径，可以通过深度优先算法，也就是沿着根节点一直访问到叶子结点，同时在访问每个结点的时候判断其是否是所要找的结点并记录下路径，如果不是并且已经走到当前分支的最后，则回溯到上一个结点走下一条分支，直至将整个二叉树遍历完或者找到路径。

首先定义一个标志flag，用来判断是否找到对应路径，初始化为false，为全局变量;

接着定义存储两条路径的vector，然后就是调用dfs函数去寻找第一条路径；

找到第一条路径后重置标志为false，然后接着调用dfs函数去寻找第二条路径；

接着通过for循环来找到两条路径中最后一个相同的结点，返回结果即可。

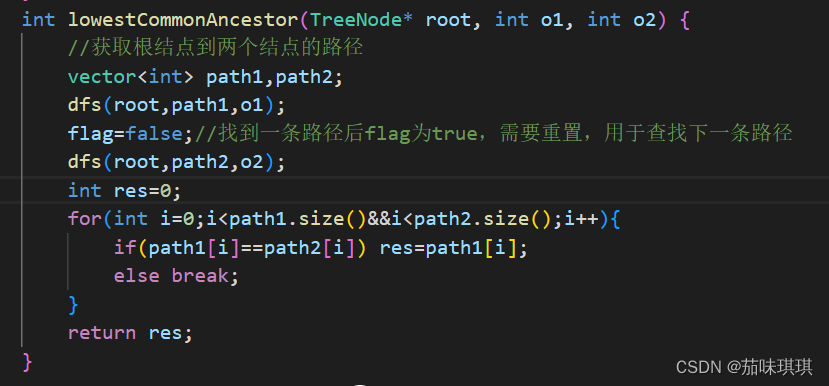
dfs函数实现，首先判断是否已经找到路径或者访问到叶子结点，是的话直接返回上一级；

否则将当前结点存入路径，判断当前结点是否就是目标结点，是的话更新标志并返回，否则递归遍历当前结点的左右子树；

如果找完了当前结点的子树没有目标结点，则弹出，回溯父结点。

---

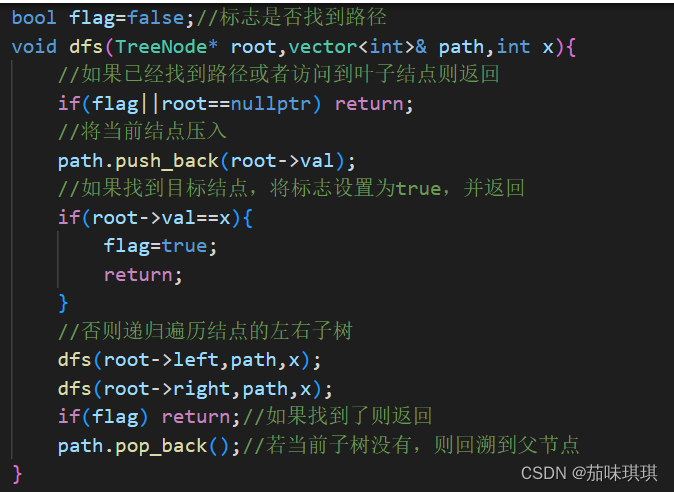
三、具体代码

#include <vector>
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param root TreeNode类 
     * @param o1 int整型 
     * @param o2 int整型 
     * @return int整型
     */
    bool flag=false;//标志是否找到路径
    void dfs(TreeNode* root,vector<int>& path,int x){
        //如果已经找到路径或者访问到叶子结点则返回
        if(flag||root==nullptr) return;
        //将当前结点压入
        path.push_back(root->val);
        //如果找到目标结点，将标志设置为true，并返回
        if(root->val==x){
            flag=true;
            return;
        }
        //否则递归遍历结点的左右子树
        dfs(root->left,path,x);
        dfs(root->right,path,x);
        if(flag) return;//如果找到了则返回
        path.pop_back();//若当前子树没有，则回溯到父节点
    }
    int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
        //获取根结点到两个结点的路径
        vector<int> path1,path2;
        dfs(root,path1,o1);
        flag=false;//找到一条路径后flag为true，需要重置，用于查找下一条路径
        dfs(root,path2,o2);
        int res=0;
        for(int i=0;i<path1.size()&&i<path2.size();i++){
            if(path1[i]==path2[i]) res=path1[i];
            else break;
        }
        return res;
    }
};