一.引言

前面提到的 K-means 是发现数据对应簇的硬聚类方法，即分配一个点其固定分配到某个簇，而高斯混合模型聚合提供了软聚类的方法，它给定数据属于 K 个簇中心的概率或可能性度量，下面介绍下高斯混合模型 Guassion Mixture Modeling 即 GMM。

二.高斯混合模型理论

1.高斯模型 GM

在介绍高斯混合模型之前，有必要先介绍下高斯模型。高斯分布是一个在数学、物理以及工程领域非常重要的概率分布，在统计学方面有很大的影响力。它指的是若随机变量 X 服从一个数学期望为 μ，方差为 σ^2 的高斯分布则记为 N(μ, σ^2)。概率密度函数为高斯分布的期望值 μ 决定了分布的位置，标准差 σ 定义了分布的幅度。最常见的分布为 N(0,1) 的正态分布：

高斯分布的数学表达公式如下：

$f(x)=\frac{1}{\sqrt{2\pi }\sigma}exp(-\frac{(x-\mu)^2}{2\sigma ^2})$

这里 μ 和 σ 都是用以表示分布的位置。高斯分布在应用上常用于图像处理、数据归纳和模式识别等方面，在对图像噪声的提取、特征分布的鉴定等方面有重要的功能。以高斯分布为基础的单高斯分布聚类模型的原理就是考察已有数据建立一个分布模型，之后通过代入样本数据计算其值是否在一个阈值范围之内。

换句话说，对于每个样本数据考察其与先构建的高斯分布模型的匹配程度，若一个数据向量在一个高斯分布模型计算的阈值之内，则认为它与高斯分布相匹配，如果不符合阈值则认为不属于该模型的聚类。

2.高斯混合模型 GMM

下面介绍多维高斯分布模型，其公式如下：

$G(x,\mu ,\sigma )=\frac{1}{\sqrt{2\pi}}exp(-\frac{(x-\mu)^{n-1})}{2\sigma})$

其中 x 是一条样本数据，μ 和 σ 分别为样本的期望和方差。通过代入计算很容易判断样本是否属于整体模型。高斯分布模型通过训练已有的数据得到，并通过更新减少认为干扰，从而实现自动对数据进行聚类计算。

为什么要提出高斯混合模型，以为内单一模型与实际数据的分布严重不符，但是几个模型混合后却能很好的描述和预测数据。就像复杂的曲线用一阶模型很难预测，但是使用多项式就能很好地拟合曲线。混合高斯模型就是在单一高斯模型的基础上发展起来的，其中每个高斯模型都代表一个类，即一个簇中心 cluster。用样本中的数据在几个高斯模型上投影，就会分别得到样本在各个类即高斯模型上的概率，然后就可以选取概率最大的类作为聚类的判定结果。

可以看到如果使用单一高斯模型，对于过度重叠的数据无法严谨区分，这时候如果有混合高斯模型，就能解决问题。高斯混合模型的原理可以用简单的一句话表述，任何样本的聚类都可以使用多个高斯模型来表示。

$Pr(x) = \sum \pi G(x,\mu ,\sigma )$

公式中 G(x,μ,σ) 是混合高斯模型的聚类中心，我们需要做的就是在样本数据已知的情况下训练获得模型参数。这里使用的是极大似然估计，用到了 EM 算法，有很多大佬都做了推导验证，这里不就做多介绍了。

三.高斯混合模型实践

1.数据准备

    val spark = SparkSession
      .builder      //创建spark会话
      .master("local")  //设置本地模式
      .appName("GaussianMixtureExample")  //设置名称
      .getOrCreate()   //创建会话变量

    // 读取数据
    val dataset = spark.read.format("libsvm").load("/Users/xudong11/sparkV3/src/main/scala/org/example/Cluster/sample_kmeans_data.txt")

数据以 libsvm 格式给出，三维数据 (x,y,z)，由于数据简单，这里肉眼可见 (1,1,1) 附近属于距离点 0,1,2 较近，而 (9,9,9) 距离点 3,4,5 较近：

0 1:0.0 2:0.0 3:0.0
1 1:0.1 2:0.1 3:0.1
2 1:0.2 2:0.2 3:0.2
3 1:9.0 2:9.0 3:9.0
4 1:9.1 2:9.1 3:9.1
5 1:9.2 2:9.2 3:9.2

2.模型训练

    // 训练 Gaussian Mixture Model，并设置参数
    val gmm = new GaussianMixture()
      .setK(2)
    val model = gmm.fit(dataset)

主要参数就是 setK 设置聚类中心，实际场景下可以随机采样一些数据 plot 出来看看大致分几类，如果数据维度较高可以使用降维的方法，关于降维之前也写过：embedding 向量的降维与可视化，大家可以参考。下面看下 GMM 的参数：

aggregationDepth - 建议的树聚合深度（>=2) (default: 2)

featuresCol - 要素列名称 (default: features)

k：混合模型中独立高斯数。必须大于1。(default: 2, current: 2)

maxIter：最大迭代次数（>=0）(default: 100)

predictionCol:预测列名称 (default: prediction)

probabilityCol：预测类条件概率的列名。注意：并非所有模型都能输出经过良好校准的概率估计值！这些概率应被视为置信度，而不是精确的概率 (default: probability)

seed：随机种子 (default: 538009335)

tol：迭代算法的收敛容差（>=0）(default: 0.01)

weightCol：权重列名称。如果未设置或为空，则将所有实例权重视为1.0 (undefined)

3.获取多个 GM

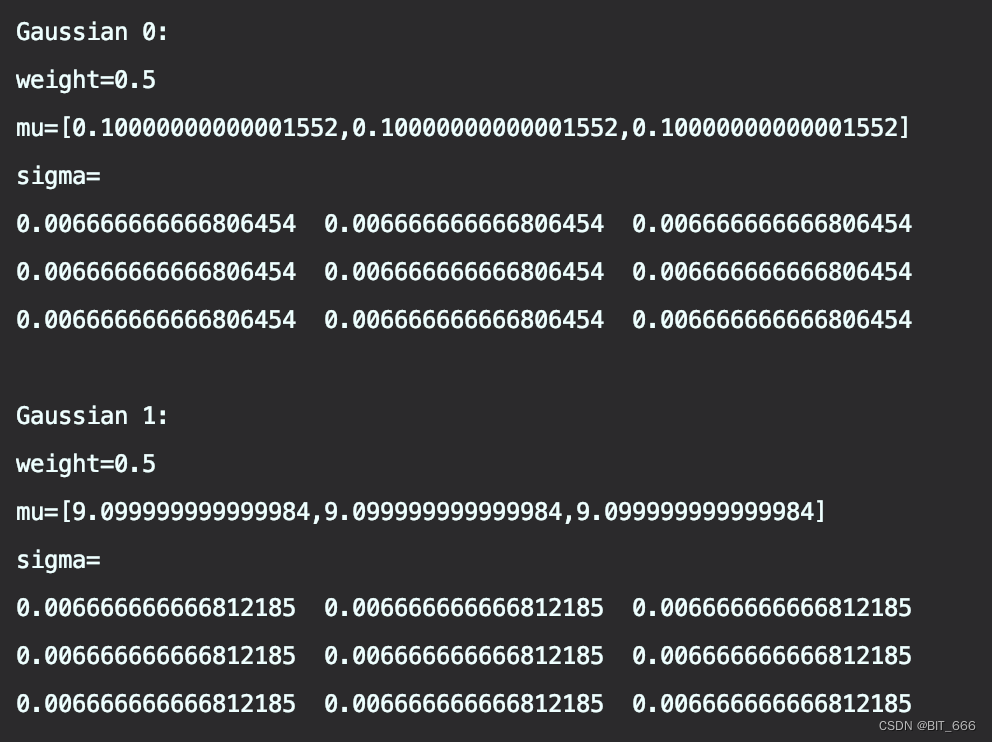
    // 逐个打印单个模型
    for (i <- 0 until model.getK) {
      println(s"Gaussian $i:\nweight=${model.weights(i)}\n" +
          s"mu=${model.gaussians(i).mean}\nsigma=\n${model.gaussians(i).cov}\n")
    }

    spark.stop()

拥有多个 GM 后，我们可以获取样本在不同聚类中心的概率值，取概率最高者作为样本对应 Cluster 即可。