【最新技术：grokking】机器学习模型是记忆还是泛化？

Do Machine Learning Models Memorize or Generalize? (pair.withgoogle.com)

机器学习模型是记忆还是泛化？

作者：Adam Pearce、 Asma Ghandeharioun、 Nada Hussein、 Nithum Thain、 Martin Wattenberg 和 Lucas Dixon

2023 年 <> 月

2021 年，研究人员在训练一系列用于玩具任务的微型模型时取得了惊人的发现。[1].他们发现了一组模型，这些模型在训练更长时间后突然从记忆训练数据转变为正确概括看不见的输入。这种现象——泛化似乎在拟合训练数据后很久突然发生——被称为grokking，并引发了一连串的兴趣。[2, 3, 4, 5, 6].

更复杂的模型在经过更长时间的训练后是否也会突然泛化？大型语言模型当然看起来对世界有丰富的理解，但它们可能只是在重复所记忆的大量文本的训练内容 [7, 8]。我们如何判断他们是在概括还是在记忆？

在本文中，我们将检查一个微型模型的训练动态，并对它找到的解决方案进行逆向工程，并在此过程中提供机械可解释性这一令人兴奋的新兴领域的说明 [9, 10]。虽然目前尚不清楚如何将这些技术应用于当今最大的模型，但随着我们逐步回答有关大型语言模型的这些关键问题，从小处开始可以更容易地发展直觉。

一、Grokking 模块化加法（Grokking Modular Addition）

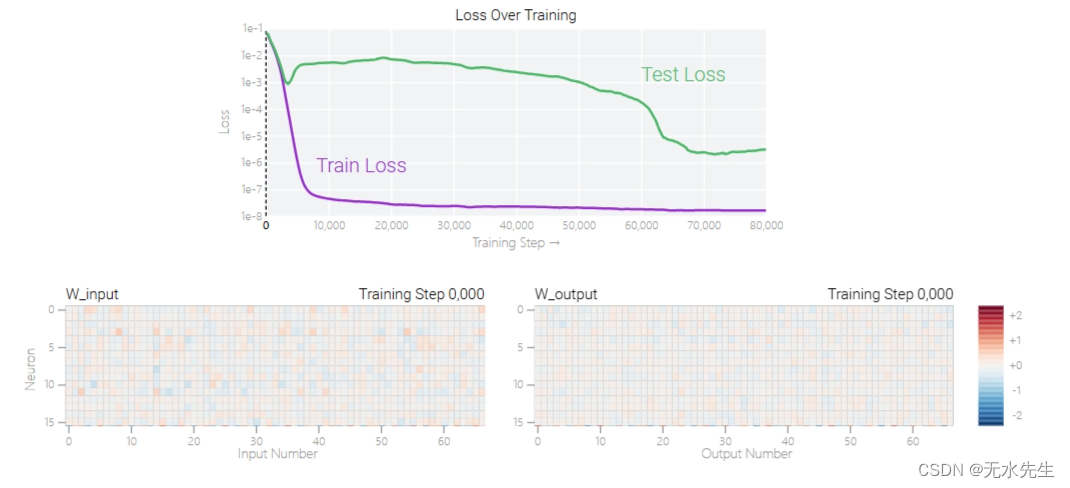
模加法本质上是 grokking 的果蝇。1 上面的折线图来自一个经过训练的预测模型a+b mod 67。我们首先随机划分所有a，b配对成测试和训练数据集。经过数千个训练步骤，训练数据用于调整模型以输出正确答案，而测试数据仅用于检查模型是否学会了通用解决方案。

https://arxiv.org/abs/2301.02679

该模型的架构同样简单： ——具有 24 个神经元的单层 MLP。模型的所有权重均显示在下面的热图中；您可以通过将鼠标悬停在上面的折线图上来查看它们在训练期间如何变化。

该模型通过选择与输入 a 和 b 相对应的 $W_{input}$ 输入的两列，然后将它们加在一起以创建由 24 个独立数字组成的向量来进行预测。接下来，它将向量中的所有负数设置为 0，最后输出 $W_{output }$ 中最接近更新向量的列。

模型的权重最初非常嘈杂，但随着测试数据的准确性增加并且模型切换到泛化，开始表现出周期性模式。训练结束时，随着输入数从 0 增加到 66，每个神经元（热图的每一行）都会在高值和低值之间循环多次。

如果我们按照神经元在训练结束时循环的频率对它们进行分组，并将每个神经元绘制成单独的线，就更容易看出：

周期性模式表明该模型正在学习某种数学结构；当模型开始解决测试示例时发生这种情况，这一事实暗示它与模型泛化有关。但为什么模型会放弃记忆解决方案呢？通用的解决方案是什么？

二、用 1 和 0 进行概括

同时解决这两个问题是很困难的。让我们做一个更简单的任务，我们知道泛化解决方案应该是什么样子，并尝试理解为什么模型最终会学习它。

我们将采用 30 个 1 和 0 的随机序列并训练我们的模型来预测前三位数字中是否有奇数个 1。例如000110010110001010111001001011 为 0，而 010110010110001010111001001011 为 1——基本上是一个稍微棘手的 XOR，带有一些干扰噪声。泛化模型应该只使用序列的前三位数字；如果模型正在记忆训练数据，它还会使用后续的分散注意力的数字 [5, 11]。

我们的模型又是一个单层 MLP，在 1,200 个序列的固定批次上进行训练。4 起初，只有训练准确度有所提高——模型会记住训练数据。与模运算一样，测试精度本质上是随机的，然后随着模型学习通用解决方案而急剧上升。

在记忆 ⏵ 时，模型看起来密集且嘈杂，大量高量级权重（显示为深红色和蓝色方块）分布在下图中 - 该模型正在使用所有输入来进行预测。随着模型概括 ⏵ 并获得完美的测试准确性，我们看到与分散注意力的数字相关的所有权重都以非常低的值显示为灰色，并且模型专注于前三位数字 - 反映了我们预期的广义结构！5

通过这个简化的示例，可以更容易地理解为什么会发生这种情况：我们推动模型在训练期间做两件事 - 输出正确标签的高概率（称为最小化损失 6）并具有低幅度的权重（称为权重衰减） 7).在模型泛化之前，训练损失实际上会略有增加，因为它交换了与输出正确标签相关的损失以具有较低的权重。

测试损失的急剧下降使得模型看起来像是突然转向泛化。但是，如果我们查看模型在训练过程中的权重，大多数模型都会在两个解决方案之间平滑地进行插值。当与分散注意力的数字相连的最后一个权重通过权重衰减被修剪时，快速泛化就会发生。

三、格罗克什么时候发生？

值得注意的是，摸索是一种偶然现象——如果模型大小、权重衰减、数据大小和其他超参数不合适，摸索就会消失。如果权重衰减太少，模型就无法避免对训练数据的过度拟合。8 添加更多的权重衰减会促使模型在记忆后进行泛化。权重衰减的增加会导致测试和训练损失同时下降；该模型直接进行概括。如果权重衰减过多，模型将无法学到任何东西。

下面，我们使用不同的超参数针对 1 和 0 任务训练了 1000 多个模型。训练过程充满噪音，因此针对每组超参数训练了九个模型。

我们可以对这个有点做作的 1 和 0 任务进行记忆和泛化——但是为什么模加法会发生这种情况呢？首先让我们更多地了解单层 MLP 如何通过构建可解释的泛化解决方案来解决模加法。

四、具有五个神经元的模块化加法

回想一下我们的模算术问题 $a+b \; mod\; 67$ 自然是周期性的，如果总和超过 67，答案就会环绕。从数学上讲，这可以通过将总和视为环绕来反映a和b绕一圈。泛化模型的权重也具有周期性模式，表明该解决方案可能会使用此属性。

我们可以训练一个更简单的模型，在问题上先行一步，构建一个嵌入矩阵，将A和B通过计算在圆上cos余弦和sin正弦对于每个可能的输入数字 $i \in \{ 0,1,...66\}$

然后我们训练 $W_{in\_proj}$ 和 $W_{out\_proj}$ 在这个单层 MLP 中.

该模型仅用五个神经元就可以完美准确地找到解决方案。

观察训练后的参数，所有神经元都收敛到大致相等的范数。如果我们直接绘制他们的正弦和余弦组件，它们基本上均匀分布在一个圆圈周围：

连接相邻的神经元 $W_{in\_proj}$ 圆圈和一个有趣的模式出现了： $W_{put\_proj}$ 绕圆旋转的速度是 $W_{in\_proj}$ 。

该解决方案如何工作的细节并不重要——请查看附录 A，了解双倍旋转如何允许模型映射输入，例如 $1+0\; mod\; 67$ 和 $2+55\; mod\; 67$ 到同一个地方——但我们找到了一个 20 个参数的结构来解决模加法。我们能否找到隐藏在我们开始的 3,216 个参数模型中的相同算法？为什么较大的模型在记忆后会切换到泛化解？

五、到处星

这是 $a+b\; mod\; 67$ ，我们开始使用的模型——它是从头开始训练的，没有内置的周期性。

与构造的解决方案不同，其中 $W_{embed}$ 绕一圈旋转一次，这个模型有很多不同的频率。

下面，我们使用离散傅里叶变换 (DFT) 隔离了频率。10 这将学习到的输入周期模式分解出来，使我们得到相当于 $W_{in\_proj}$ 和 $W_{put\_proj}$
从构造的解决方案。对于每个神经元，这给出了cos 和sin从 1 到 33 的每个可能的周期频率的值。我们上面显示的波形图使用它通过找到神经元的最大频率来将神经元分组为频率cos 和sin 所有频率的值。

就像在 1 和 0 任务中一样，随着模型泛化 ⏵ ，权重衰减会促使这种表示变得更加稀疏。

按最终训练频率对神经元进行分组，并绘制 cos和sin对于每个神经元的 DFT 组件，我们看到构建的解决方案中出现了相同的星形。

这个经过训练的模型使用与我们构建的解决方案相同的算法！下面显示了每个频率下神经元生成的输出的贡献，我们可以看到它们在计算 $cos\frac{2\pi (a+b)freq}{67}$ .12

请注意，当测试损失在 45,000 步的短暂稳定期后有所改善时，频率为 7 的神经元组会发生什么——它们开始转变为星形，并且它们的输出更接近于波。

为了在不使用更高权重的情况下降低损失（这将受到权重衰减的惩罚），该模型利用相长干扰，使用多个频率。 [10]频率 4、5、7 和 26 并没有什么神奇之处——点击下面的其他训练运行可以看到学到的该算法的变体。

六、开放性问题

虽然我们现在对单层 MLP 用于解决模加法的机制以及它们在训练过程中出现的原因有了深入的了解，但仍然存在许多关于记忆和泛化的有趣的悬而未决的问题。

6.1 哪种模型约束最有效？

- 即使增加了权重衰减，实际上也不会导致模算术的泛化。至少必须分解一个矩阵：

我们观察到，采用离散傅里叶变换后，泛化解是稀疏的，但折叠矩阵具有高范数。这表明直接权重衰减 $W_{output}$ 和 $W_{output}$ 没有为任务提供正确的归纳偏差。

从广义上讲，权重衰减确实会导致多种模型不再记忆训练数据 [12, 13]。其他有助于避免过度拟合的技术包括 dropout、较小的模型，甚至数值不稳定的优化算法 [14]。这些方法以复杂、非线性的方式相互作用，使得很难先验预测最终导致泛化。

崩溃 $W_{embed}$ $W_{in\_proj}$ 代替， $W_{out\_proj}$ , $W_{embed}^T$ 例如，对某些设置有帮助，但对另一些设置有害：

6.2 为什么记忆比概括更容易？

一种理论：记忆训练集的方法可能比泛化解决方案多得多。因此从统计上看，记忆应该更有可能首先发生，特别是如果我们没有或很少进行正规化的话。正则化技术（例如权重衰减）将某些解决方案优先于其他解决方案，例如，优先选择“稀疏”解决方案而不是“密集”解决方案。

最近的工作表明泛化与结构良好的表示相关[15]。然而，这不是必要条件；一些没有对称输入的 MLP 变体在求解模加法时学习的“循环”表示较少 [4]。我们还观察到，结构良好的表示并不是泛化的充分条件。这个小模型（没有权重衰减的情况下训练）开始泛化，然后切换到使用周期性嵌入进行记忆。

甚至可以找到模型开始泛化的超参数，然后切换到记忆，然后再切换回泛化！

6.3 更大的型号怎么样？

摸索是否会发生在接受现实世界任务训练的较大模型中？早期的观察报道了小型 Transformer 和 MLP 算法任务中的 grokking 现象 [1,10,4]。随后，Grokking 被发现可以用于涉及特定超参数范围内的图像、文本和表格数据的更复杂的任务 [2, 16]。能够执行多种类型任务的最大模型也有可能在训练期间以不同的速度处理许多事情[17]。

在摸索发生之前进行预测也取得了有希望的结果。尽管有些需要泛化解决方案 [10] 或整体数据域 [18] 的知识，但有些仅依赖于训练损失的分析 [19]，并且也可能适用于更大的模型 - 希望我们能够构建工具以及可以告诉我们模型何时重复记忆的信息以及何时使用更丰富的模型的技术。

理解模块化加法的解决方案并非易事。我们有希望理解更大的模型吗？一条前进的道路——就像我们离题到 20 参数模型和更简单的布尔奇偶校验问题一样——是：1）用更多的归纳偏差和更少的移动部件训练更简单的模型，2）用它们来解释更大模型中难以理解的部分有效，3）根据需要重复。我们相信，这可能是一种富有成效的方法，可以更好地理解更大的模型，并且可以补充旨在使用更大的模型来解释更小的模型的努力以及解开内部表征的其他工作[20,21,22]。此外，这种机械的可解释性方法最终可能有助于识别模式，这些模式本身可以简化或自动揭示神经网络学习的算法。

制作人员
感谢 Ardavan Saeedi、Crystal Chen、Emily Reif、Fernanda Viégas、Kathy Meier-Hellstern、Mahima Pushkarna、Minsuk Chang、Neel Nanda 和 Ryan Mullins 对本文的帮助。