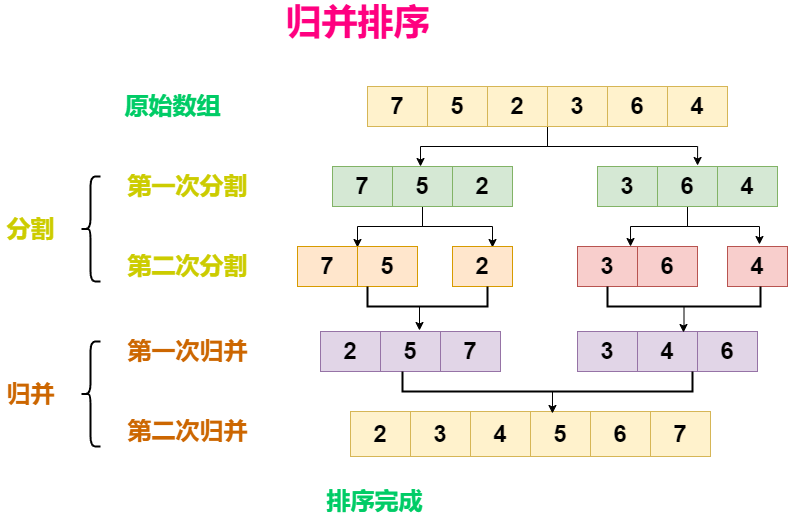
假设Level 0为内存中的Buffer,容量为 B B B,层与层之间的条目数量差 T T T 倍
Tiered
- Level 1共有 T T T 个runs,每个run的容量均为 B B B
- Level 2共有 T T T 个runs,每个run的容量均为 T ⋅ B T\cdot B T⋅B
- Level n共有 T T T 个runs,每个run的容量均为 T n − 1 ⋅ B T^{n-1}\cdot B Tn−1⋅B
合并的过程:当Level 0满时,层内排序后写入Level 1。若Level 1此刻也满了,将整个Level 1归并排序后写入Level 2
合并的触发时机: 新的run加入后level满容量时(即runs的数量达到上限时)
操作代价
point query
O
(
L
⋅
T
⋅
e
−
M
f
i
l
t
e
r
s
N
)
O(L\cdot T\cdot e^{-\frac{M_{filters}}{N}})
O(L⋅T⋅e−NMfilters),其中
L
L
L 为层数,
e
−
M
f
i
l
t
e
r
s
N
e^{-\frac{M_{filters}}{N}}
e−NMfilters 是假阳率
解释:每层有
T
T
T 个runs,runs之间范围可能重合,因此每个run都要读取,而每个run通过读取栅栏指针来确定目标Key所在的页面,因此每个run最多涉及2次I/O,也就是
O
(
1
)
O(1)
O(1)。布隆过滤器帮助减少一次I/O
update
O
(
L
P
)
O(\frac{L}{P})
O(PL),其中
P
P
P 表示一个页面能够存储的条目数量
解释:一个被更新的条目从Level 0到与最后一层的旧条目合并,共经历了
L
L
L 次复制(读取、写回),但每次I/O共有
P
P
P 个条目,因此可以均摊
Leveled
- Level 1共有 1 个run,容量为 T ⋅ B T\cdot B T⋅B
- Level 2共有 1 个run,容量为 T 2 ⋅ B T^2\cdot B T2⋅B
- Level n共有 1 个run,容量为 T n ⋅ B T^{n}\cdot B Tn⋅B
合并的过程:当Level 0满时,与Level 1进行层间归并排序后写入Level 1,若Level 1此刻也满了,继续将Level 1和Level 2归并排序
合并的触发时机: 上一层满时
操作代价
point query
(
L
⋅
e
−
M
f
i
l
t
e
r
s
N
)
(L\cdot e^{-\frac{M_{filters}}{N}})
(L⋅e−NMfilters)
解释:每层只有 1 个run
update
O
(
T
⋅
L
P
)
O(\frac{T\cdot L}{P})
O(PT⋅L)
解释:每层的run会在与上一层合并
T
T
T 次后满,而每次合并都会产生复制
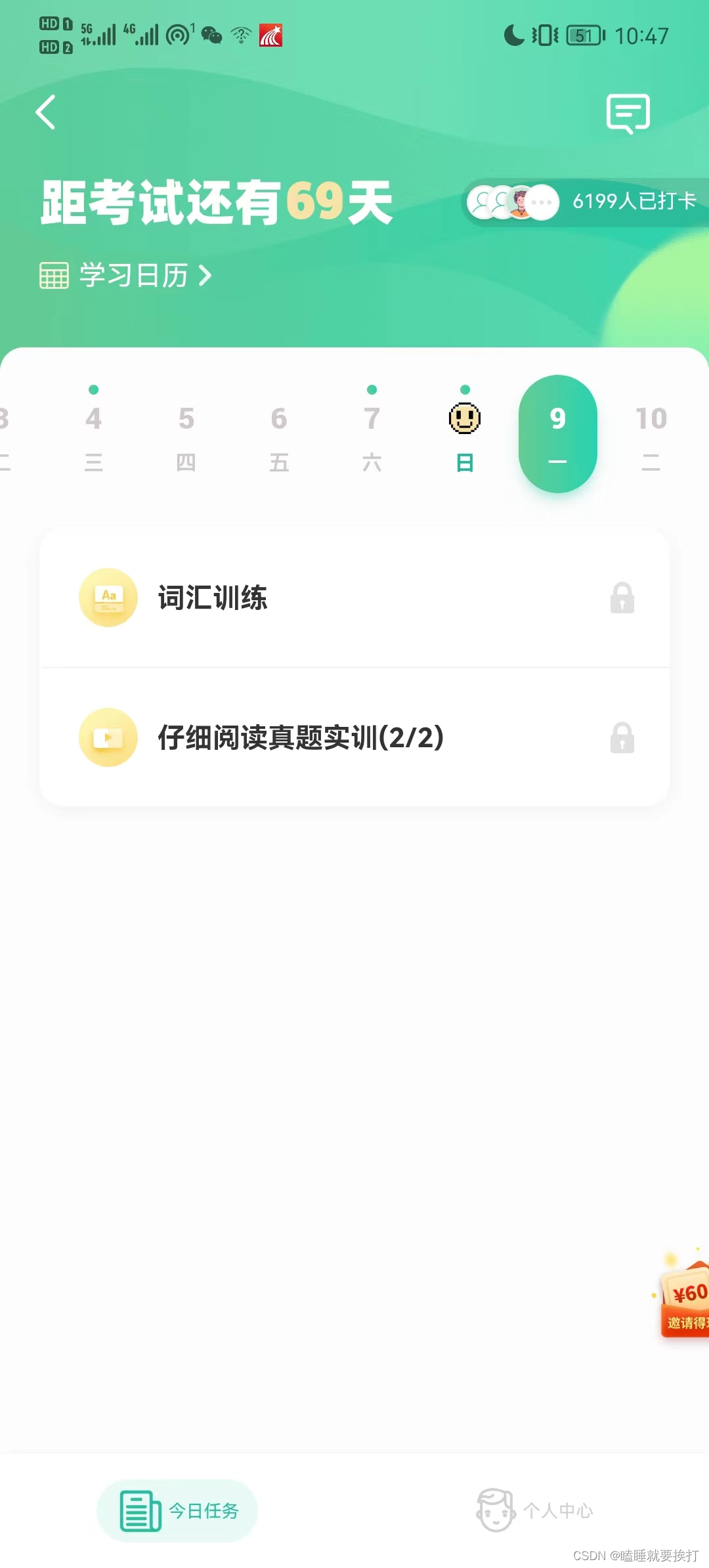
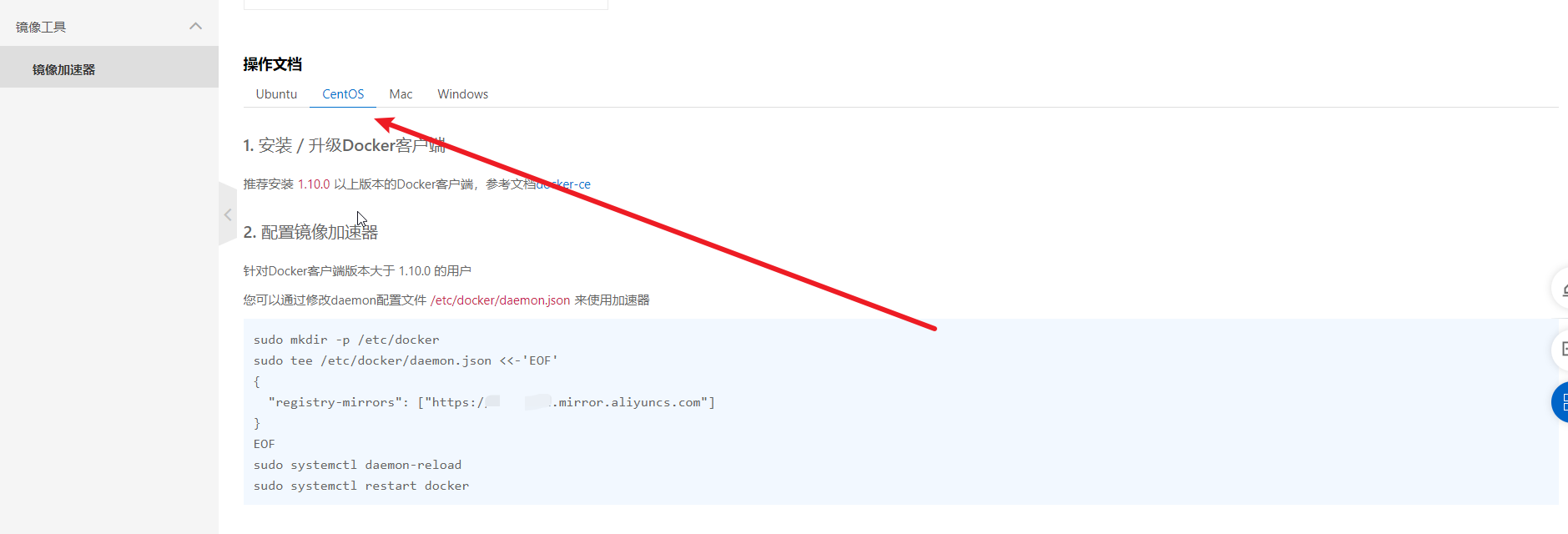
示意图






![[NewStarCTF 2023 公开赛道] week1 Crypto](https://img-blog.csdnimg.cn/6e6aba16652347f2881a2605a48caf6b.png)