Deep learning of free boundary and Stefan problems论文阅读复现
- 摘要
- 1. 一维一相Stefan问题
- 1.1 Direct Stefan problem
- 1.2 Inverse Type I
- 1.3 Inverse Type II
- 2. 一维二相Stefan问题
- 2.1 Direct Stefan problem
- 2.2 Inverse Type I
- 2.3 Inverse Type II
- 3. 二维一相Stefan问题
- 参考
摘要
在这项工作中,作者提出了一个基于物理信息神经网络的多网络模型,来解决一类一般的正和逆自由边界问题,称为Stefan问题。具体地说,用两个深度神经网络来近似未知解以及任何移动边界。作者提供了三个案例研究(一维一相Stefan问题,一维二相Stefan问题,二维一相Stefan问题),每个案例分别研究了正问题和两个逆问题,相关代码可以在https://github.com/PredictiveIntelligenceLab/DeepStefan获得。
复现代码环境:
conda create -n tensorflow1x python=3.6
conda activate tensorflow1x
pip install tensorflow==1.15.5 -i https://pypi.tuna.tsinghua.edu.cn/simple
pip install pandas -i https://pypi.tuna.tsinghua.edu.cn/simple
pip install seaborn -i https://pypi.tuna.tsinghua.edu.cn/simple
pip install scipy -i https://pypi.tuna.tsinghua.edu.cn/simple
pip install matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple
1. 一维一相Stefan问题

- Direct Stefan problem: 已知 u 0 , g ( t ) , s 0 , h 1 ( t ) , h 2 ( t ) u_0, g(t), s_0, h_1(t), h_2(t) u0,g(t),s0,h1(t),h2(t) ,求解 u ( x , t ) : Ω → R . u(x,t):\Omega \rightarrow \mathbb{R}. u(x,t):Ω→R.
- Inverse Type I: 希望找到满足方程(3.1),(3.2),(3.5),(3.6)的温度分布 u ( x , t ) u(x,t) u(x,t) ,也希望当移动边界 s ( t ) s(t) s(t)已知时重构 Dirichlet 和 Neumann 边界条件。
- Inverse Type II: 给出域 Ω \Omega Ω 中的一些温度测量值,试图找到满足方程 (3.1),(3.4),(3.5) 的温度解 u ( x , t ) u(x,t) u(x,t),并确定移动边界 s(t) 的未知位置。

1.1 Direct Stefan problem
方程 (3.1)-(3.6) 中已知变量由 (3.7)-(3.8) 表示,(3.9) 和 (3.10) 分别是该问题的精确解和移动边界的解。
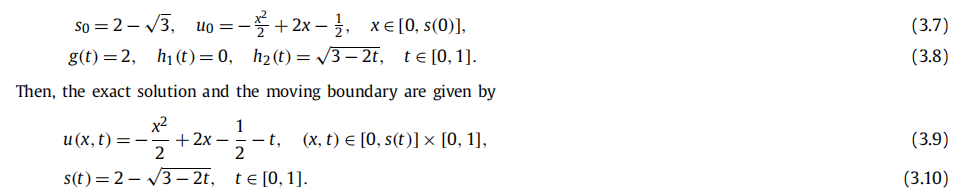
文章作者使用两个独立的神经网络近似潜在的
u
(
x
,
t
)
u(x,t)
u(x,t) 和
s
(
t
)
s(t)
s(t),训练40000epoch,一个epoch从初始条件
x
=
0
,
x=0,
x=0, 边界条件
t
=
0
,
t=0,
t=0, 和内部
Ω
∈
Ω
∗
=
[
0
,
1
]
×
[
0
,
1
]
\Omega \in \Omega^*=[0,1]\times[0,1]
Ω∈Ω∗=[0,1]×[0,1] 中各随机选择一个batch_size(128)数据点进行训练,没有用到真解。由于
s
(
t
)
s(t)
s(t) 在我们的问题设置中是未知的,所以我们不能简单地在
(
0
,
s
(
t
)
×
(
0
,
t
)
(0,s(t)\times(0,t)
(0,s(t)×(0,t) 中进行采样点。处理这一技术问题的一种方法是对整个计算域
Ω
∗
\Omega^*
Ω∗ 中的配置点进行采样,这是先验已知的,但然后通过将预测解
u
θ
(
x
,
t
)
u_{\theta}(x,t)
uθ(x,t) 限制在域
(
0
,
s
β
(
t
)
×
(
0
,
t
)
(0,s_{\beta}(t)\times(0,t)
(0,sβ(t)×(0,t) 来关注物理解。损失函数如下:
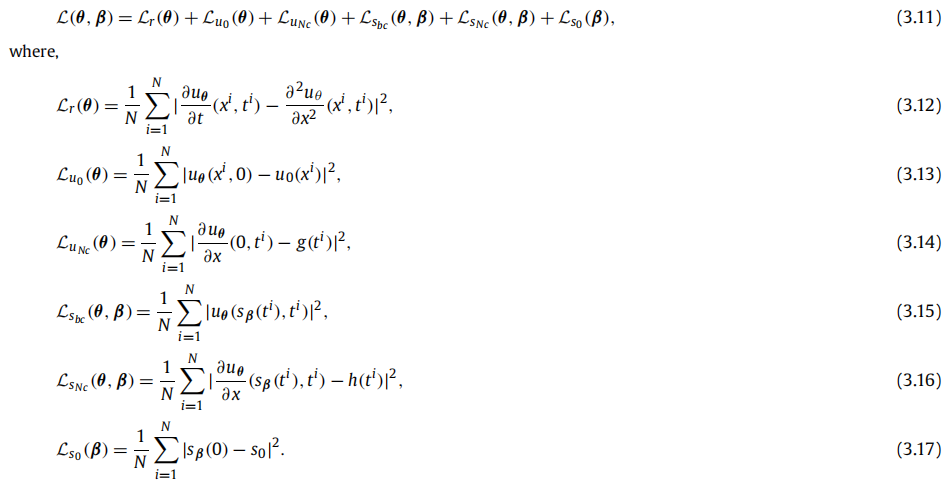
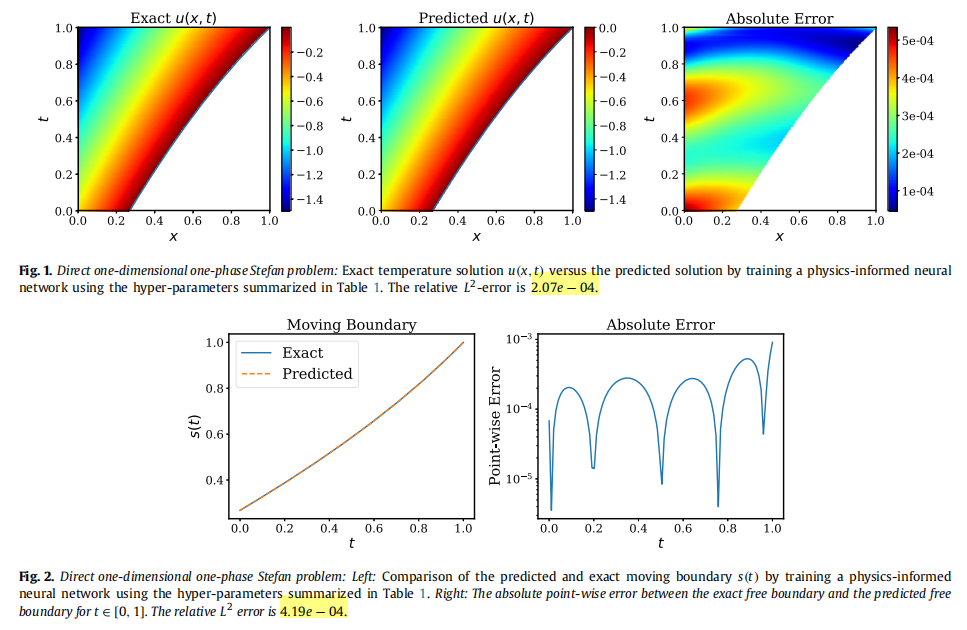
论文中实验结果:
复现的实验结果:

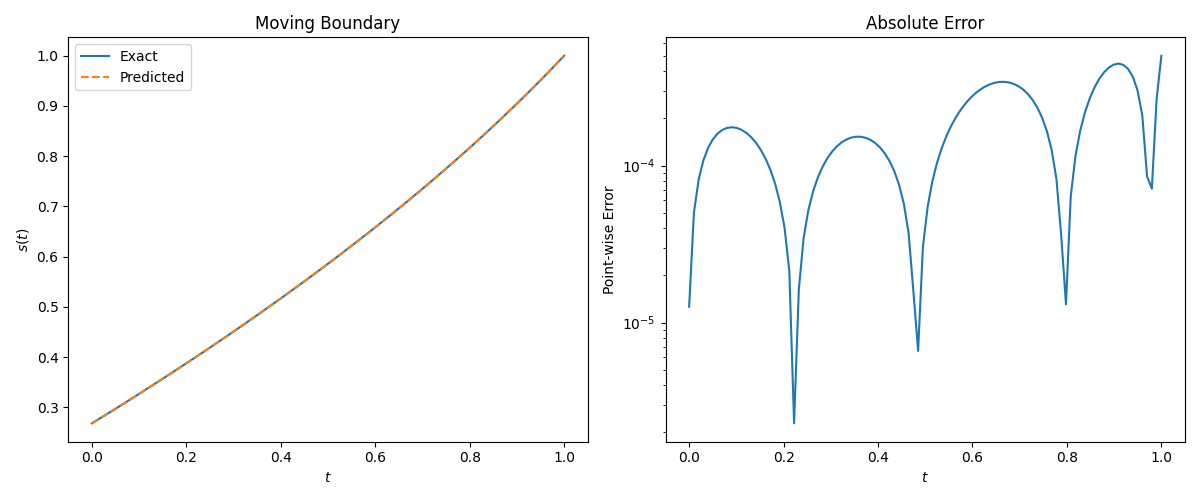
The u(x,t) relative
L
2
L_2
L2-error is 4.64e-04.
The s(t) relative
L
2
L_2
L2-error is 3.32e-04.
1.2 Inverse Type I
这种类型的逆问题也叫移动边界设计问题,这里的目标是找到满足方程 (3.1)-(3.6) 的解,并在给定自由边界
s
(
t
)
s(t)
s(t) 信息的情况下恢复狄利克雷和诺伊曼边界条件
(
3.18
)
(3.18)
(3.18) 。

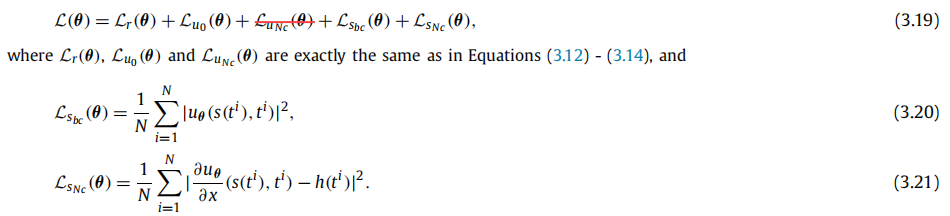
论文中实验结果:

复现实验结果:
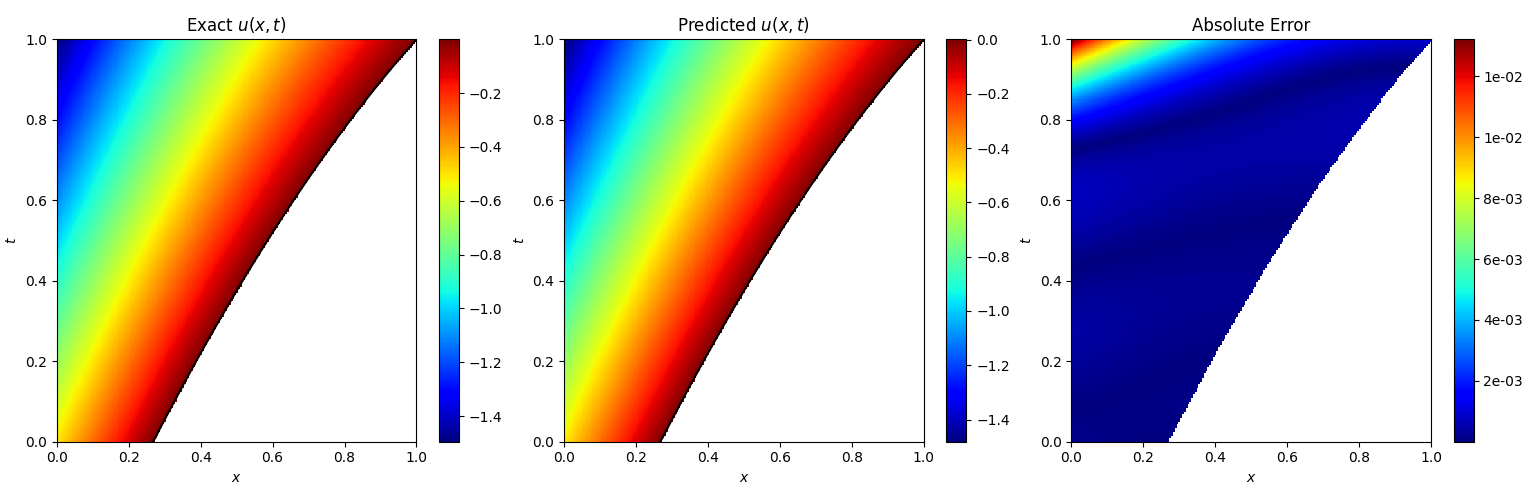
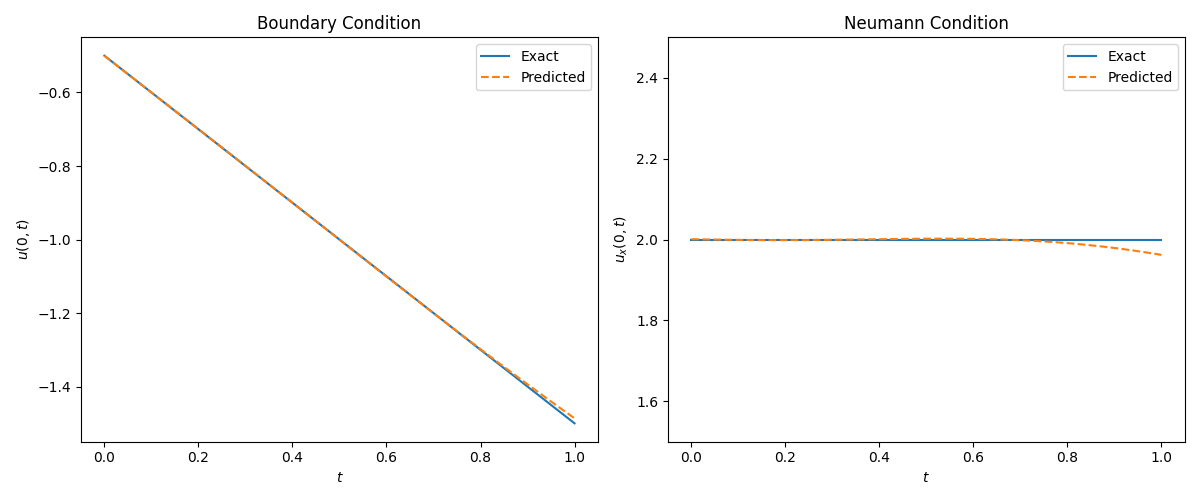
The u(x,t) relative
L
2
L_2
L2-error is 2.48e-03.
The
u
θ
u_{\theta}
uθ(0,t) relative
L
2
L_2
L2-error is 3.32e-03.
The
∂
u
θ
∂
x
\frac{\partial u_{\theta}}{\partial x}
∂x∂uθ(0,t) relative
L
2
L_2
L2-error is 5.39e-03.
1.3 Inverse Type II
给定少量测试点 { u ( x d a t a j , t d a t a j ) } j = 1 M \{u(x_{data}^j, t_{data}^j)\}_{j=1}^M {u(xdataj,tdataj)}j=1M,我们想得到在域 Ω \Omega Ω 上符合热方程(3.1)的 u ( x , t ) u(x,t) u(x,t),以及未知边界符合(3.4)-(3.6)的 s ( t ) s(t) s(t),这样不需要任何初始或边界条件,这是接近许多现实的应用,这样的信息可能难以获得。为了解决这个问题,依然用两个神经网络 u θ ( x , t ) , s β ( t ) u_{\theta}(x,t),s_{\beta}(t) uθ(x,t),sβ(t) 近似 u ( x , t ) , s ( t ) u(x,t),s(t) u(x,t),s(t)。损失函数如下所示:
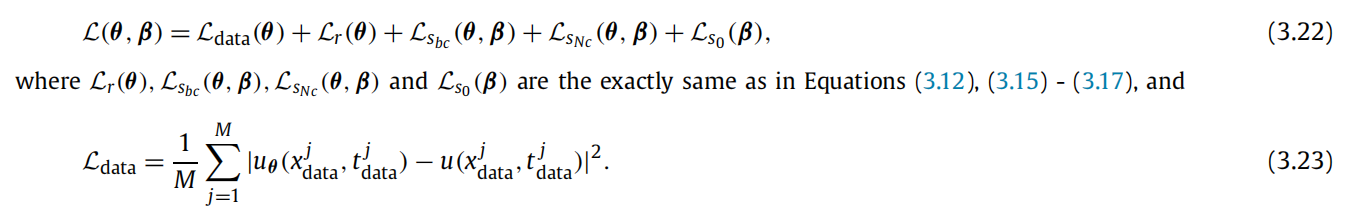
论文中实验结果:
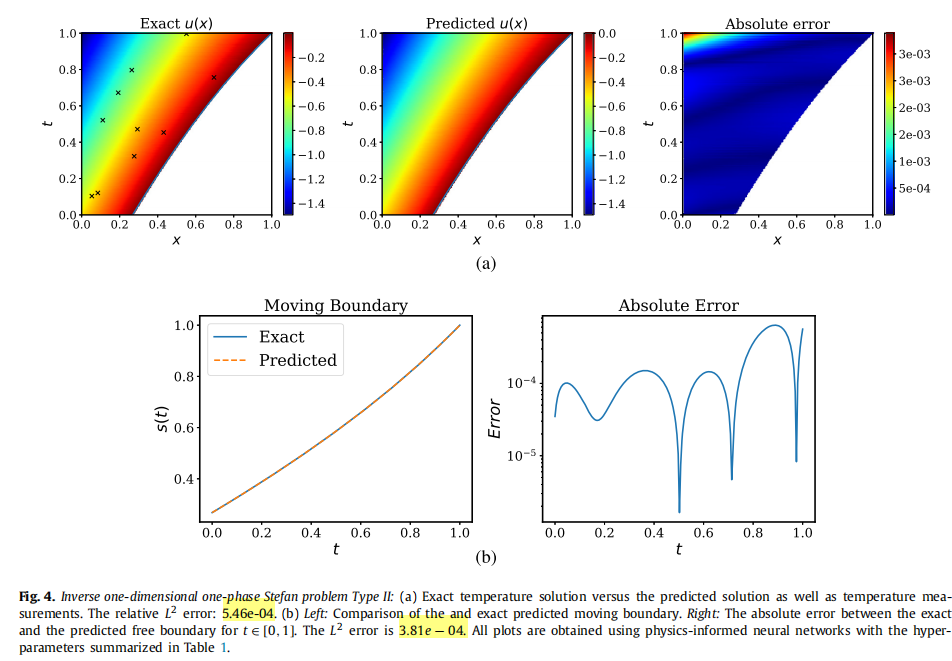
复现实验结果:
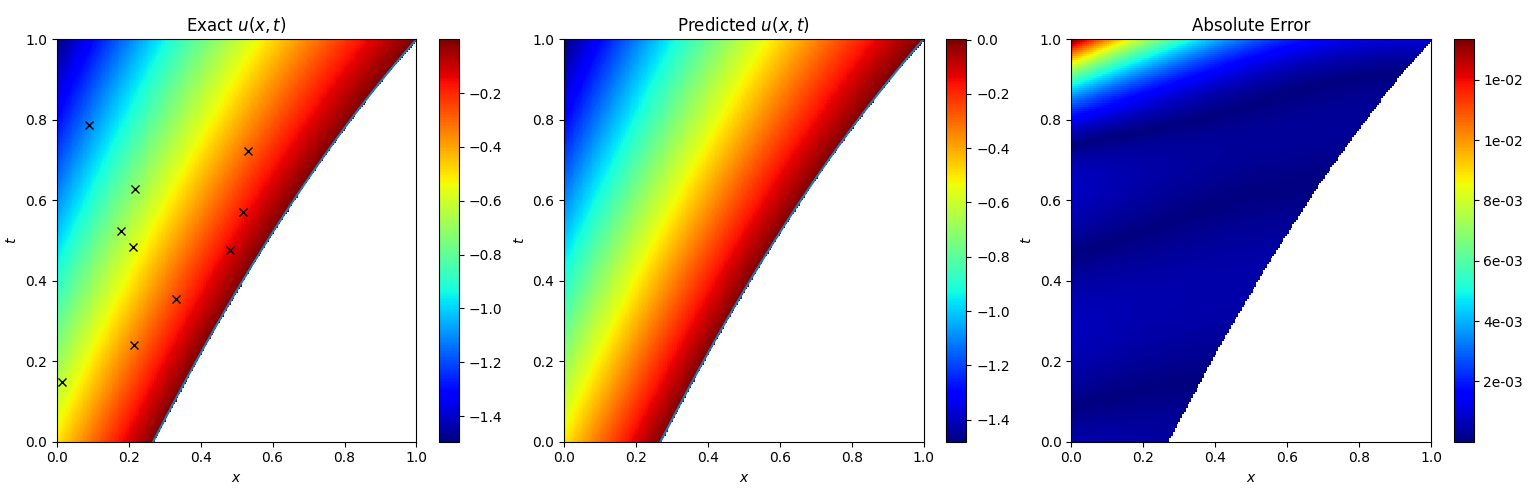
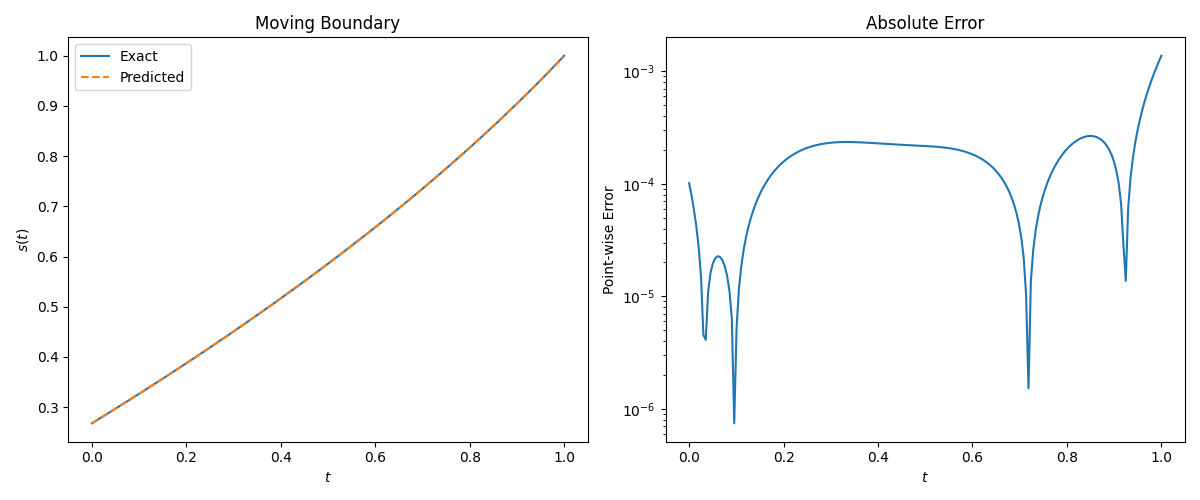
The u(x,t) relative
L
2
L_2
L2-error is 2.83e-03.
The s(t) relative
L
2
L_2
L2-error is 4.11e-04.
2. 一维二相Stefan问题
2.1 Direct Stefan problem
复现实验结果:
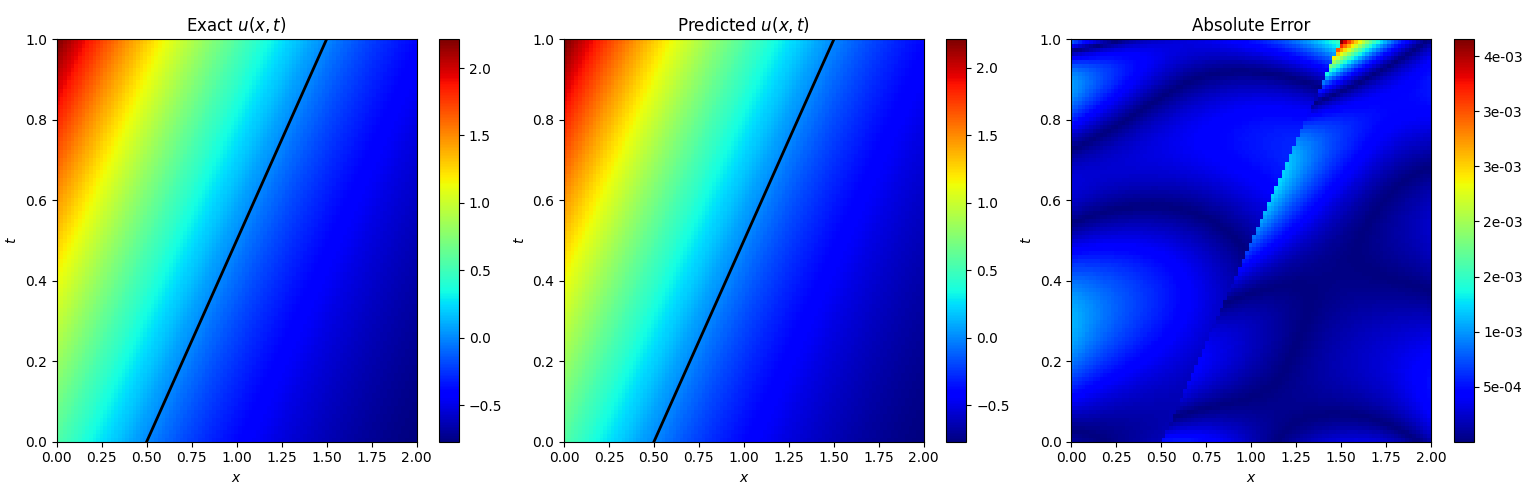
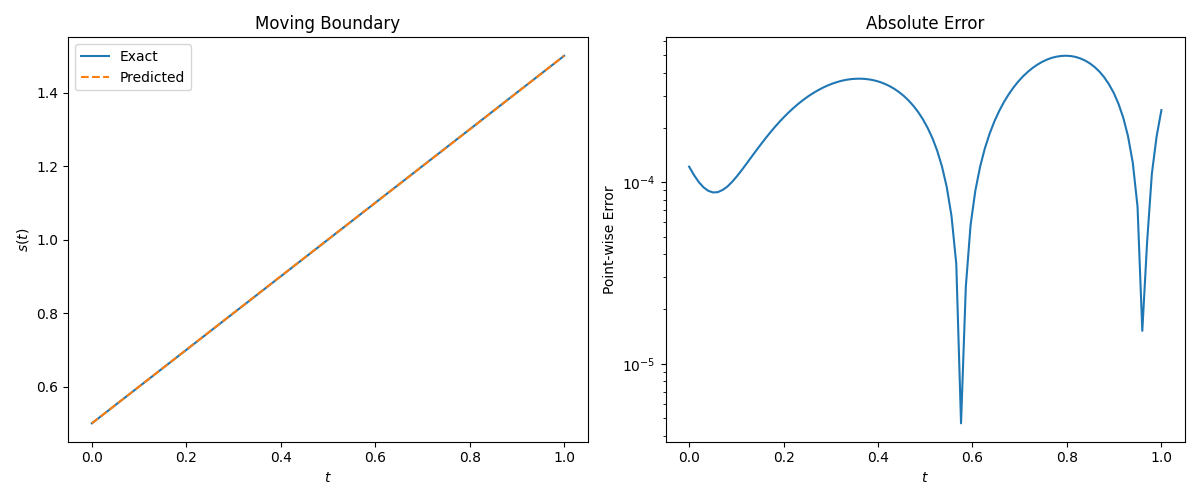
The u(x,t) relative
L
2
L_2
L2-error is 6.35e-04.
The s(t) relative
L
2
L_2
L2-error is 2.78e-04.
2.2 Inverse Type I
复现实验结果:
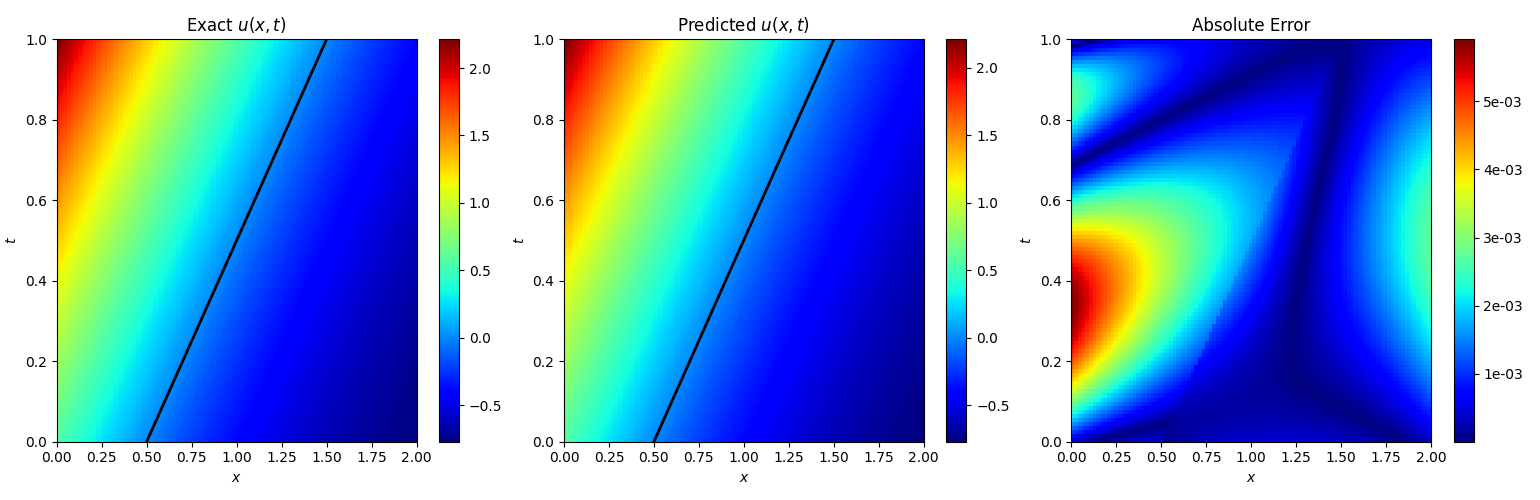
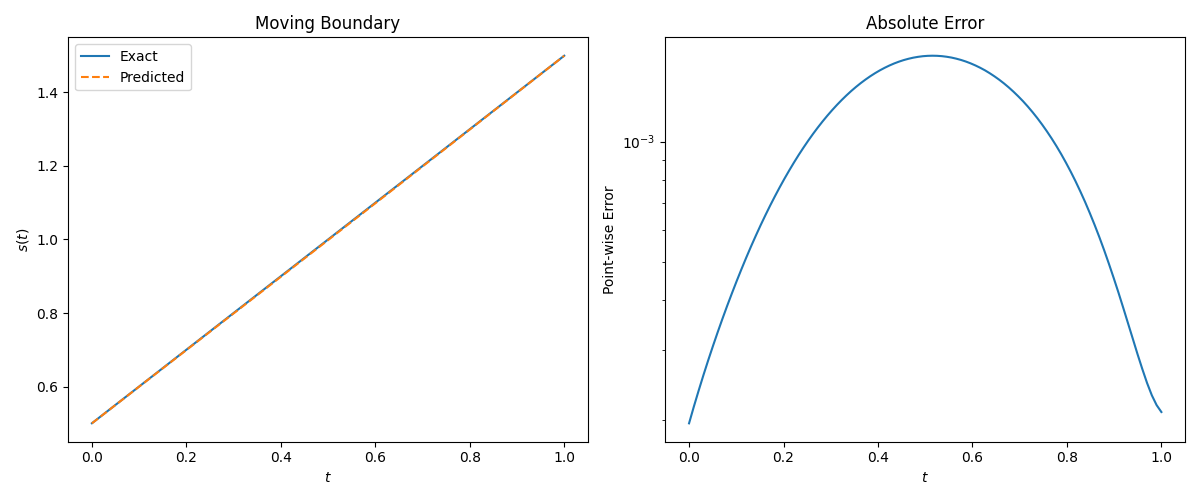
The u(x,t) relative
L
2
L_2
L2-error is 2.71e-03.
The s(t) relative
L
2
L_2
L2-error is 1.06e-03.
2.3 Inverse Type II
复现实验结果:
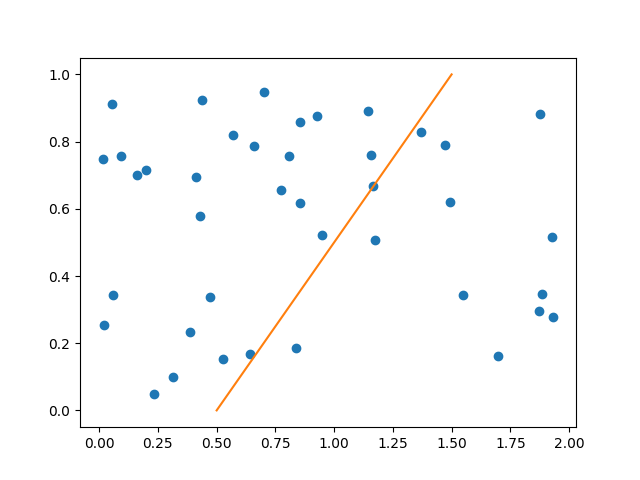
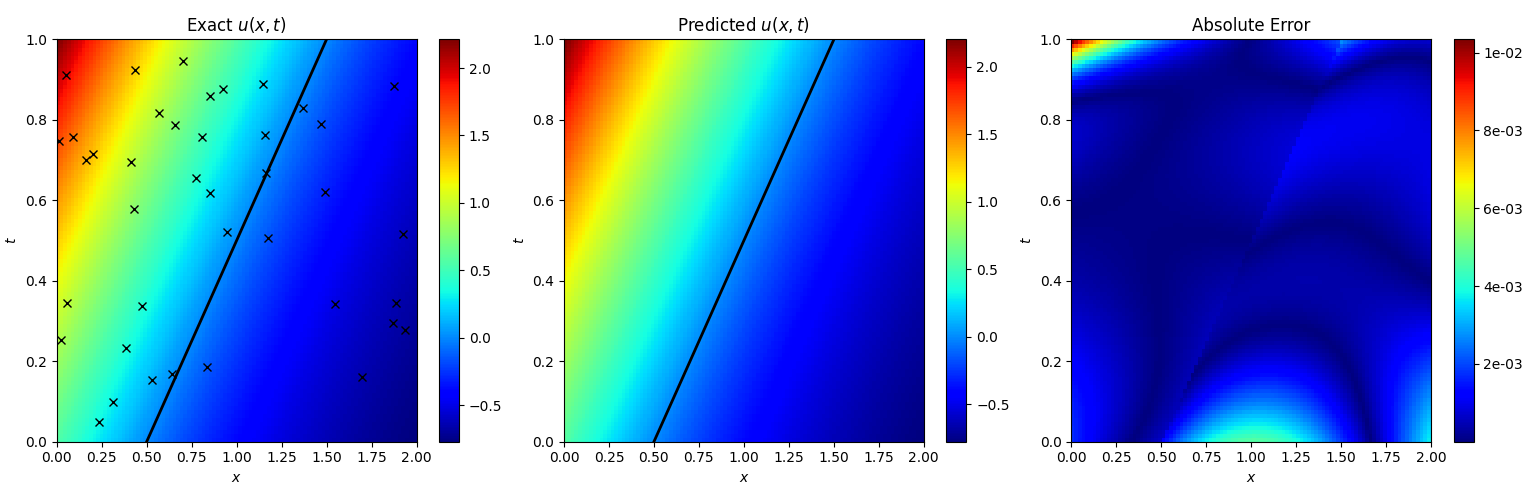
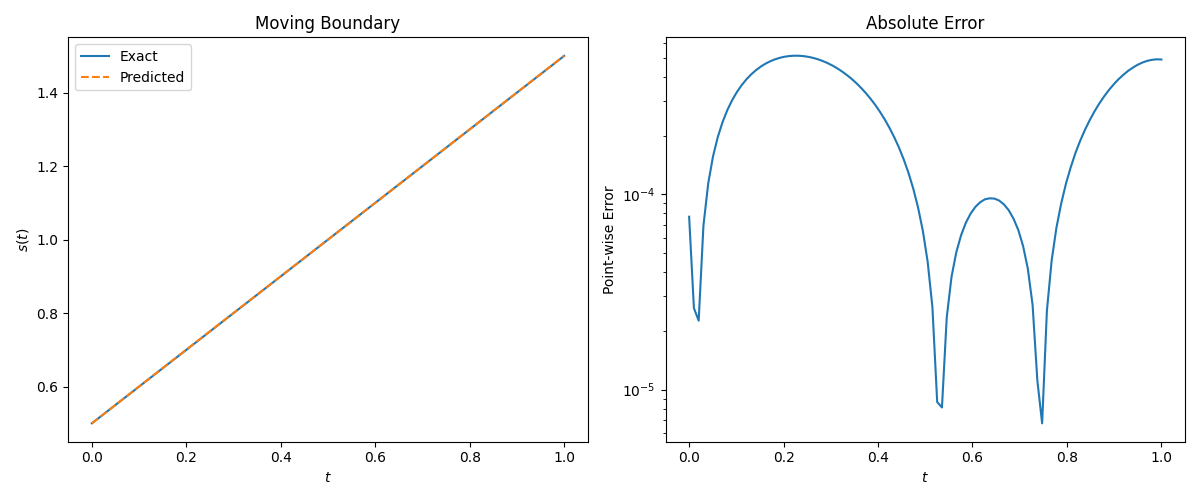
The u(x,t) relative
L
2
L_2
L2-error is 1.71e-03.
The s(t) relative
L
2
L_2
L2-error is 2.94e-04.
3. 二维一相Stefan问题
略
参考
[1] Deep learning of free boundary and Stefan problems
[2] https://github.com/PredictiveIntelligenceLab/DeepStefan