Eastern Exhibition【中位数 距离和的最小值】
题意翻译
二维平面上有 n 个点，要找一个点，使得所有点到它的曼哈顿距离（ x 和 y 的坐标差距之和）之和最小。请问有几个满足该要求的点？
输入输出样例
输入 #1
6
3
0 0
2 0
1 2
4
1 0
0 2
2 3
3 1
4
0 0
0 1
1 0
1 1
2
0 0
1 1
2
0 0
2 0
2
0 0
0 0
输出 #1
1
4
4
4
3
1

说明/提示
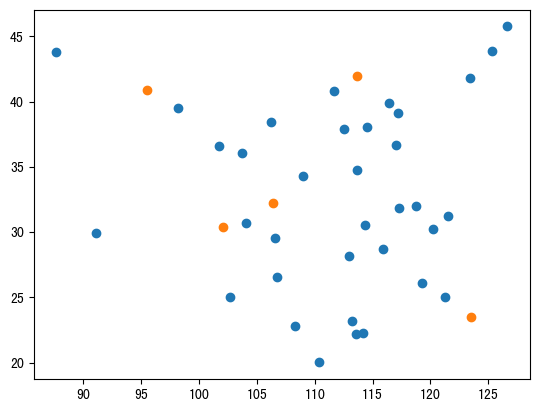
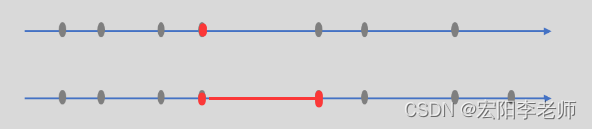
下面是示例测试用例的图像。蓝点代表房屋，绿点代表展览的可能位置。
第一个测试案例。

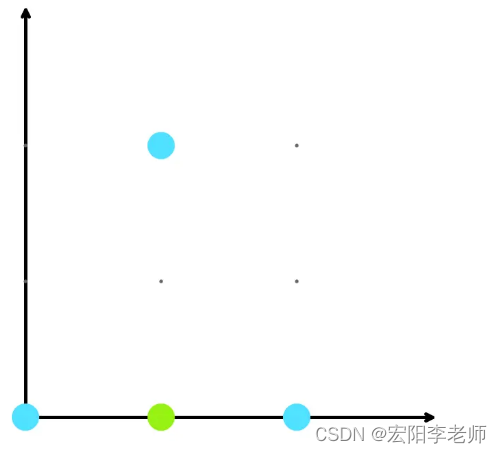
第二个测试案例。

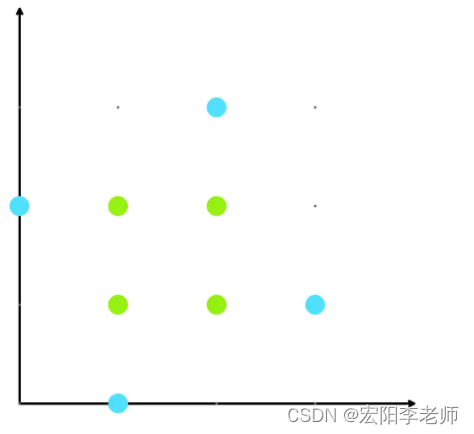
第三个测试案例。

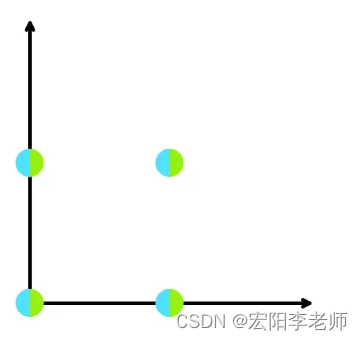
第四个测试案例。

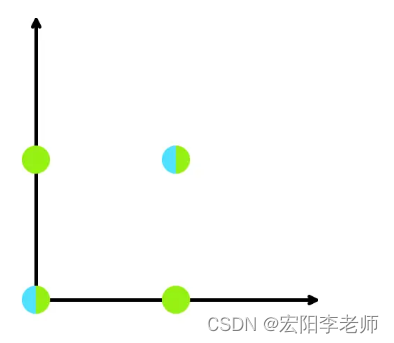
第五个测试案例。

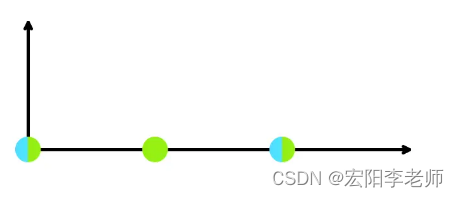
第六个测试案例。这里两座房子都位于(0,0)(0,0)。

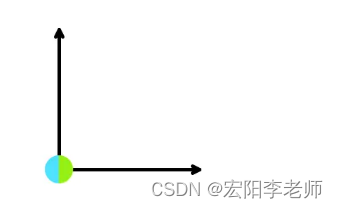
解题思路分析：
遇到二维问题时可以先看看能不能将其转化为一维问题。
可以发现，当改变 × 坐标时，y坐标的距离和不变，因此可以将其转化为一维问题，即分别求出x轴和y轴最优点的数量，然后将其相乘就是答案。
x=a[n/2]-a[(n-1)/2]+1
y=b[n/2]-b[(n-1)/2]+1
ans=x*y

#include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int k,n,a[N],b[N];
int main()
{	
	cin>>k;
	long long x,y;
	while(k--){
		cin>>n;
		for(int i=0;i<n;i++) 
			cin>>a[i]>>b[i];
		sort(a,a+n);
		sort(b,b+n);
		x=a[n/2]-a[(n-1)/2]+1;
		y=b[n/2]-b[(n-1)/2]+1;
		cout<<x*y<<endl;
	}
    return 0;
}