【数据结构与算法】二叉树的实现以及二叉排序数的实现

news2024/11/25 2:35:50

目录

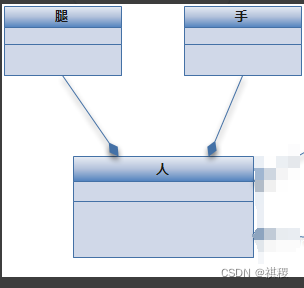
通过数组实现二叉树

通过链表实现二叉树

排序二叉树的实现

通过数组实现二叉树

该实现方式只能用于完全二叉树，因为如果是普通二叉数的话，数组中会出现空隙，会导致空间的利用率会降低。

实现思路：

        因为假设一个父节点的下标为parentIndex，那么他的左子节点的下标就为2parentIndex，他的右子节点的下标就为2parentIndex+1。

        所以想要获取一个左子节点时只需将她父节点的下标通过<<1即可（相当于* 2）获得左子节点的下标，获取右子节点时与之相同，不过在<<1的同时在+1。

        而将一个数组直接转换为二叉树只需将数组下标向右移一位即可，下标从1开始。

/**
 * @author CC
 * @version 1.0
 * @since2023/10/7
 * 使用数组实现二叉树
 */
public class BinaryToArrayTree<E> {
    private Object[] elementData = null;

    /**
     * 有参构造 直接将一个数组变为二叉树
     * @param elements
     */
    public BinaryToArrayTree(E[] elements) {
        elementData = new Object[elements.length + 1];

        for (int i = 0, index = 1; i < elements.length; i++, index++) {
            elementData[index] = elements[i];
        }
    }

    /**
     * 获取该下标的值
     * @param index
     * @return
     */
    public E get(int index){
        return (E) elementData[index];
    }

    /**
     * 获取该下标的左子节点的值
     * @param index
     * @return
     * @throws Exception
     */
    public E left(int index) throws Exception {
        if ((index<<1)>=elementData.length){
            throw new Exception("左孩子节点不存在！");
        }
        return (E) elementData[index<<1];
    }

    /**
     * 获取该下标的右子节点的值
     * @param index
     * @return
     * @throws Exception
     */
    public E right(int index) throws Exception {
        if (((index<<1)+1)>=elementData.length){
            throw new Exception("右孩子节点不存在！");
        }
        return (E) elementData[(index<<1)+1];
    }
 }

测试

public class BATest {
    public static void main(String[] args) throws Exception {
        String[] array ={"A","B","C","D","E","F","G","H"};
        BinaryToArrayTree<String> binaryTree =new BinaryToArrayTree<>(array);
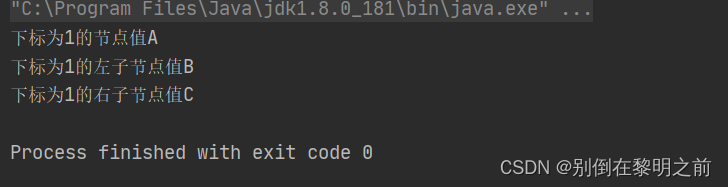
        System.out.println("下标为1的节点值"+binaryTree.get(1));
        System.out.println("下标为1的左子节点值"+binaryTree.left(1));
        System.out.println("下标为1的右子节点值"+binaryTree.right(1));
    }
}

测试结果

通过链表实现二叉树

/**
 * @author CC
 * @version 1.0
 * @since2023/10/7
 * 使用链表实现二叉树
 */
public class BinaryToListTree<E> {
    TreeNode<E> root;//根节点

    public BinaryToListTree(E val) {
        root = new TreeNode<E>(val);
    }

    /**
     * 存入左节点
     * @param parent 父节点
     * @param val 左节点的值
     * @return
     */
    public TreeNode<E> left(TreeNode<E> parent, E val) {
        TreeNode<E> newNode = new TreeNode<>(val);
        parent.left = newNode;
        return newNode;
    }

    /**
     * 存入右节点
     * @param parent 父节点
     * @param val 右节点的值
     * @return
     */
    public TreeNode<E> right(TreeNode<E> parent, E val) {
        TreeNode<E> newNode = new TreeNode<>(val);
        parent.right = newNode;
        return newNode;
    }

    /**
     * 先序遍历
     * @param root 根节点
     */
    public void preOrder(TreeNode root){
        if (root==null){
            return;
        }
        System.out.print(root.data);
        preOrder(root.left);
        preOrder(root.right);
    }

    /**
     * 中序遍历
     * @param root 根节点
     */
    public void inOrder(TreeNode root){
        if (root==null){
            return;
        }
        inOrder(root.left);
        System.out.print(root.data);
        inOrder(root.right);
    }

    /**
     * 后序遍历
     * @param root 根节点
     */
    public void postOrder(TreeNode root){
        if (root==null){
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.data);
    }


    /**
     * 层序遍历
     * @param root 根节点
     */
    public void levelOrder(TreeNode root){
        if (root ==null){
            return;
        }
        Queue<TreeNode> queue =new LinkedList<>();
        queue.offer(root);
        while (true){
            TreeNode cur = queue.poll();
            if (cur==null){
                return;
            }

            System.out.print(cur.data);
            if (cur.left!=null){
                queue.offer(cur.left);
            }
            if (cur.right!=null){
                queue.offer(cur.right);
            }
        }
    }


    /**
     * 节点类
     * @param <E>
     */
    public static class TreeNode<E> {
        E data;//数据
        TreeNode<E> left;//左节点
        TreeNode<E> right;//右节点

        public TreeNode() {
        }

        public TreeNode(E val) {
            this.data = val;
        }
    }
}

测试

public class BLTest {
    public static void main(String[] args) {
        BinaryToListTree<String> tree =new BinaryToListTree<>("A");

        //将B C 分别存入A 的左右节点
        BinaryToListTree.TreeNode<String> b= tree.left(tree.root, "B");
        BinaryToListTree.TreeNode<String> c= tree.right(tree.root, "C");

        //将D E 分别存入B 的左右节点
        BinaryToListTree.TreeNode<String> d= tree.left(b, "D");
        BinaryToListTree.TreeNode<String> e= tree.right(b, "E");

        //将F G 分别存入C 的左右节点
        BinaryToListTree.TreeNode<String> f= tree.left(c, "F");
        BinaryToListTree.TreeNode<String> g= tree.right(c, "G");

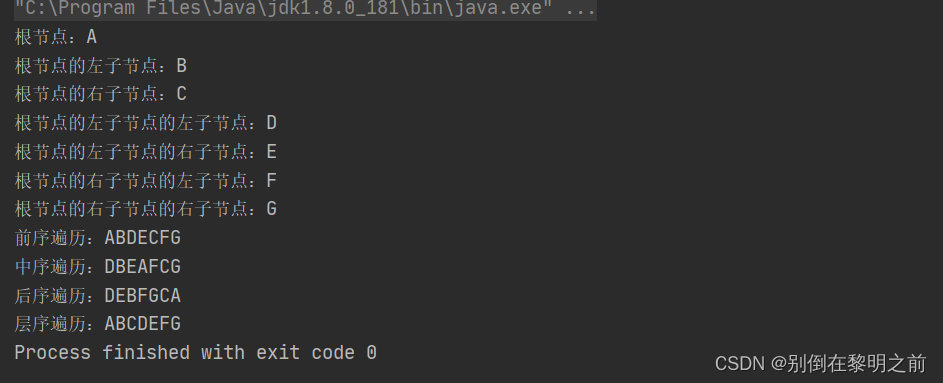
        System.out.println("根节点："+tree.root.data);
        System.out.println("根节点的左子节点："+tree.root.left.data);
        System.out.println("根节点的右子节点："+tree.root.right.data);
        System.out.println("根节点的左子节点的左子节点："+tree.root.left.left.data);
        System.out.println("根节点的左子节点的右子节点："+tree.root.left.right.data);
        System.out.println("根节点的右子节点的左子节点："+tree.root.right.left.data);
        System.out.println("根节点的右子节点的右子节点："+tree.root.right.right.data);


        System.out.print("前序遍历：");
        tree.preOrder(tree.root);
        System.out.println();

        System.out.print("中序遍历：");
        tree.inOrder(tree.root);
        System.out.println();

        System.out.print("后序遍历：");
        tree.postOrder(tree.root);
        System.out.println();

        System.out.print("层序遍历：");
        tree.levelOrder(tree.root);

    }

}

测试结果

排序二叉树的实现

实现思路：

二叉排序数他的实现思路是父节点的左子节点一定小于父节点，而父节点的右子节点一定大于父节点，所以排序二叉树的中序遍历就是就是该二叉树节点从小到大的排序。他的最大值就是根节点的最右子节点，而最小值就是根节点的最左子节点。

/**
 * 二叉排序树
 * @author CC
 * @version 1.0
 * @since2023/10/8
 */
public class BinarySortTree {

    TreeNode root;//根节点

    /**
     * 初始化方法
     * @param arr
     */
    public void init(int[] arr){
        for (int i : arr) {
            insert(new TreeNode(i));
        }
    }

    /**
     * 中序遍历
     * @param node
     */
    public void inOrder(TreeNode node){
        if (node==null){
            return;
        }
        inOrder(node.left);
        System.out.print(node.data+" ");
        inOrder(node.right);
    }


    /**
     * 插入节点
     * @param newNode
     */
    public void insert(TreeNode newNode){
        TreeNode currentNode =this.root;//查找过程中的当前节点
        TreeNode parent =null;//插入节点的父节点

        //查找新节点的插入位置
        while (currentNode !=null){
            parent =currentNode;
            if (newNode.data<currentNode.data){
                currentNode =currentNode.left;
            }else {
                currentNode = currentNode.right;
            }
        }

        //查找到的最终节点作为新节点的父节点
        newNode.parent =parent;

        //如果该该树为空 没有父节点
        if (parent==null){
            this.root =newNode;
        }else {
            if (newNode.data<parent.data){
                parent.left =newNode;
            }else {
                parent.right=newNode;
            }
        }
    }

    /**
     * 通过节点值和节点查找
     * @param currentNode
     * @param data
     * @return
     */
    private TreeNode search(TreeNode currentNode,Integer data){
        if (currentNode==null){
            return null;
        }
        if (data<currentNode.data){
            return search(currentNode.left,data);
        }else if (data>currentNode.data){
            return search(currentNode.right,data);
        }else {
            return currentNode;
        }
    }

    /**
     * 通过节点值查找查找 默认从根节点开始查找
     * @param data
     * @return
     */
    public TreeNode search(Integer data){
        TreeNode resultNode =search(this.root,data);
        return resultNode;
    }


    /**
     * 查找最大值
     * @param currentNode
     * @return
     */
    public TreeNode max(TreeNode currentNode){
        if (currentNode==null){
            return null;
        }
        TreeNode parent =null;

        while (currentNode!=null){
            parent =currentNode;
            currentNode=currentNode.right;
        }
        return parent;
    }


    /**
     * 查找最小值
     * @param currentNode
     * @return
     */
    public TreeNode min(TreeNode currentNode){
        if (currentNode ==null){
            return null;
        }
        TreeNode parent =null;

        while (currentNode!=null){
            parent=currentNode;
            currentNode =currentNode.left;
        }
        return parent;
    }

    /**
     * 节点类
     */
    static class TreeNode{
        Integer data; //节点数据
        TreeNode left; //左子节点
        TreeNode right; //右子节点
        TreeNode parent; //父节点

        public TreeNode(){
        }

        public TreeNode(Integer val){
            this.data =val;
        }
    }
}

测试

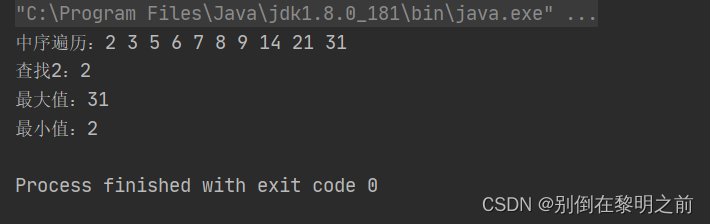
public class BSTest {
    public static void main(String[] args) {
        BinarySortTree bst =new BinarySortTree();
        bst.init(new int[] {2,8,6,9,31,3,5,21,7,14});

        System.out.print("中序遍历：");
        bst.inOrder(bst.root);
        System.out.println();

        BinarySortTree.TreeNode node = bst.search(2);
        System.out.println("查找2："+node.data);

        System.out.println("最大值："+bst.max(bst.root).data);
        System.out.println("最小值："+bst.min(bst.root).data);
    }
}

测试结果

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1071221.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

原码反码补码移码的介绍和计算

原码反码补码移码的介绍和计算

1.原码 原码的定义&#xff1a;十进制数据的二进制表示形式就是原码。 &#xff08;1&#xff09;原码的最左边那位是符号位&#xff0c;其他位为数据位&#xff0c;符号位是0则为正数&#xff0c;符号位是1则为负数。 &#xff08;2&#xff09;一个byte有8bit&#xff0c;最…
阅读更多...
Node-RED系列教程-25node-red获取天气

Node-RED系列教程-25node-red获取天气

安装节点：node-red-contrib-weather 节点图标如下： 使用说明：node-red-contrib-weather (node) - Node-RED 流程图中填写经度和纬度即可。 演示： json内容： {
阅读更多...
jmeter 请求发送加密参数

jmeter 请求发送加密参数

最近在做http加密接口&#xff0c;请求头的uid参数及body的请求json参数都经过加密再发送请求&#xff0c;加密方式为&#xff1a;ase256。所以&#xff0c;jmeter发送请求前也需要对uid及json参数进行加密。我这里是让开发写了个加密、解密的jar&#xff0c;jmeter直接调用这个…
阅读更多...
CRM系统如何自动分配线索

CRM系统如何自动分配线索

分配线索是销售部门很重要的一项工作&#xff0c;大量的线索中潜藏着许多企业未来的忠实客户。如果将大把的线索通过手工的方式分配给多个销售人员是一件棘手的事&#xff0c;就要借助CRM系统自动分配线索。 你的企业是否也面临这些难题&#xff1a; 1.渠道多线索多&#xff…
阅读更多...
点击、拖拉拽开发可视化大屏，网友直呼不可思议

点击、拖拉拽开发可视化大屏，网友直呼不可思议

可视化大屏既足够炫酷&#xff0c;又能快速整合多业务系统数据&#xff0c;可视化分析数据&#xff0c;是一种可运用于博览中心、会议中心、监控中心、企业大屏看板等场景的常用数据可视化分析形式。但可视化大屏虽然好用&#xff0c;在开发制作上却难倒了不少人&#xff0c;直…
阅读更多...
汇编实现点灯实验

汇编实现点灯实验

.text .global _start _start: 设置GPIOF寄存器的时钟使能LDR R0,0X50000A28LDR R1,[R0]ORR R1,R1,#(0x1<<5)STR R1,[R0]设置GPIOE寄存器的时钟使能LDR R0,0X50000A28LDR R1,[R0] 从r0为起始地址的4字节数据取出放在R1ORR R1,R1,#(0x1<<4) 第4位设置为1STR R1,[…
阅读更多...
vue3 + typescript + vite + naive ui + tailwindcss + jsx 仿苹果桌面系统

vue3 + typescript + vite + naive ui + tailwindcss + jsx 仿苹果桌面系统

基于 vue3.x typescript vite naive ui tailwindcss jsx vue-router pinia&#xff0c;项目使用 tsx 作为模版输出&#xff0c;全程没有使用vue提供的SFC&#xff0c; 仿macos桌面前端项目&#xff0c;开源免费模版&#xff0c;希望减少工作量和学习新技术&#xff0c;希…
阅读更多...
javascript制作简单的富文本，基本功能都实现，除了上传图片只能用URL

javascript制作简单的富文本，基本功能都实现，除了上传图片只能用URL

//所有的图标用的字符&#xff0c;以后可以换成网上的css-icon图标库的图标&#xff0c;再设置一下css样式即可简单的使用 //这里所有的标签元素都是直接获取&#xff0c;没有使用委托&#xff0c;如果使用委托性能会更好&#xff0c;这里只做了简单的清理&#xff0c;让内存回…
阅读更多...
操作系统对内存的管理：分配与回收，虚拟内存，内存容量的扩充，内存保护，补充（链接方式、装入方式）

操作系统对内存的管理：分配与回收，虚拟内存，内存容量的扩充，内存保护，补充（链接方式、装入方式）

内存&#xff1a;即内存条&#xff0c;也称主存储器&#xff08;简称主存&#xff09;&#xff0c;用于存放数据。 为了缓和CPU和外存&#xff08;磁盘&#xff09;的速度矛盾&#xff0c;外存的程序先放入内存才能被CPU处理。 内存地址从0开始&#xff0c;每个内存地址对应一…
阅读更多...
以太网基础学习（三）——UDP协议

以太网基础学习（三）——UDP协议

一、UDP协议概述 UDP&#xff08;User Datagram Protocol&#xff0c;用户数据报协议&#xff09;是一种无连接协议&#xff0c;它不像TCP协议那样需要在发送和接收数据前进行握手和释放&#xff0c;而是直接把数据发送出去&#xff0c;也不会对数据进行可靠传输和流量…
阅读更多...
ARM_汇编流水灯

ARM_汇编流水灯

ARM_汇编流水灯 .text .global _start _start: 设置GPIOE寄存器的时钟使能ldr r0,0x50000A28ldr r1,[r0] 从r0为起始地址的4字节数据取出存入r1orr r1,r1,#(0x01<<4) 第4位设置为1 表示开启时钟使能orr r1,r1,#(0x01<<5) 第5位设置为1 表示开启时钟使能str r1…
阅读更多...
求推荐好用的可视化大屏软件？强推奥威BI

求推荐好用的可视化大屏软件？强推奥威BI

在博览中心、会议中心、监控中心等场合下&#xff0c;经常看到很多炫酷的企业可视化大屏&#xff0c;将复杂的企业数据可视化展现&#xff0c;高大上、实用性一个不缺。那&#xff0c;可视化大屏做得好的软件有哪些&#xff1f;首推奥威BI软件。 奥威BI软件&#xff1a;零编程…
阅读更多...
ST表(RMQ问题)

ST表(RMQ问题)

ST表能够O(1)地解决区间[l,r]之间最值问题 1.建表&#xff0c;首先明白ST[i][j]&#xff0c;表示的是区间[i, i(1<<j)-1]的最值&#xff0c;区间大小为2^j。首先初始化ST[i][0]a[i]。 void init&#xff08;&#xff09;{for(int i1; i<n; i){ST[i][0]a[i];} } 因为…
阅读更多...
如何配置防火墙？看这篇就够了

如何配置防火墙？看这篇就够了

大家好&#xff0c;我是老杨。 在互联网时代&#xff0c;网络安全的问题不用多说了&#xff0c;配置防火墙是非常必要的。 在网络的世界里&#xff0c;要由防火墙过滤的就是承载通信数据的通信包。 防火墙是位于内部网和外部网之间的屏障&#xff0c;也是系统的第一道防线。…
阅读更多...
06.数据解析-xpath

06.数据解析-xpath

1、什么是xpath ​ XPath (XML Path Language) 是一门在 HTML\XML 文档中查找信息的语言&#xff0c;可用来在 HTML\XML 文档中对元素和属性进行遍历。 W3School官方文档&#xff1a;http://www.w3school.com.cn/xpath/index.asp 2、认识xml 知识点&#xff1a; html和xml…
阅读更多...
如何使用 Xunit 框架进行单元测试和集成测试

如何使用 Xunit 框架进行单元测试和集成测试

在软件开发过程中&#xff0c;测试是至关重要的一环。测试驱动开发&#xff08;Test-Driven Development&#xff0c;TDD&#xff09;是一种常用的开发方法论&#xff0c;它强调在编写代码之前先编写测试用例&#xff0c;然后通过不断迭代的方式来实现功能。为了帮助开发者更好…
阅读更多...
解决项目报错：@org.springframework.beans.factory.annotation.Autowired(required=true)

解决项目报错：@org.springframework.beans.factory.annotation.Autowired(required=true)

项目使用mybatis&#xff0c;启动时报错&#xff1a; Description: Field toolsDetailsService in com.cvit.applet.controller.ToolsDetailsController required a bean of type com.cvit.applet.mapper.ToolsDetailsMapper that could not be found. The injection point has…
阅读更多...
上门按摩小程序｜同城上门按摩软件开发｜上门按摩系统；

上门按摩小程序｜同城上门按摩软件开发｜上门按摩系统；

上门按摩小程序的开发具有许多优势&#xff0c;下面就给大家介绍下按摩小程序功能: 上门按摩小程序的优势 方便快捷&#xff1a;上门按摩小程序提供在线预约服务&#xff0c;用户可以通过手机随时随地预约按摩师上门服务&#xff0c;避免了传统预约方式的繁琐和不确定性。 个性…
阅读更多...
面向对象设计-UML六种箭头含义

面向对象设计-UML六种箭头含义

目录 UML概述UML语义UML表示法 六种常用关系标识方法泛化实现依赖关联聚合组合 本文参考文章 https://blog.csdn.net/qq_25091281/article/details/123801862 UML概述 UML (Unified Modeling Language)为面向对象软件设计提供统一的、标准的、可视化的建模语言。适用于描述以…
阅读更多...
Vue、js底层深入理解笔记

Vue、js底层深入理解笔记

文章目录 1. Vue中列表组件的key值有什么作用&#xff1f;2. [1, 2, 3].map(parseInt)结果 1. Vue中列表组件的key值有什么作用&#xff1f; 这个是修改数组的情况下 还有增删的情况下 删除12&#xff0c;添加67 结果 带key的dom节点发生改变&#xff0c;内容未改变 不带key…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023