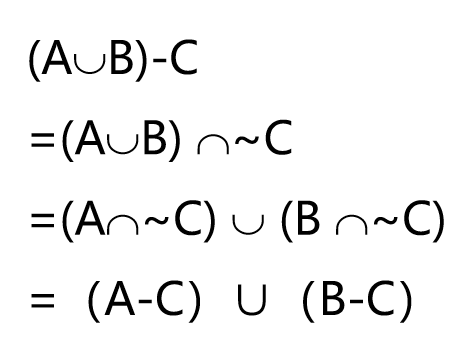集合的运算等式:


常用的集合运算不等式:
 、
、
试题
A,B,C是集合,证明:(A-B)-C=A-(B∪C)
【答案】
设A、B、C是集合,证明 (A∪B)-C=(A-C)∪(B-C)。
【答案】
已知A={1,2,3},A-B={1,2},则A∩~B=_______。
【答案】 {1,2}
设集合A={1,2,3,4,5,6},集合B={x丨x=n2+1,n∈N,x<20},则A∪B=________。
【答案】{1,2,3,4,5,6,10,17},
因为集合B={1,2,5,10,17},所以A∪B={1,2,3,4,5,6,10,17}。
对任意集合A、B、C,推导出下列集合等式成立的充要条件
(1)(A-B)∪(A-C)=A
(2)(A-B)∪(A-C)=∅【答案】
(1)
(A-B)∪(A-C)
=(A∩~B)∪(A∩~C)
= A∩(~B∪~C)
= A∩~(B∩C)
= A-(B∩C)
因此,当且仅当A∩B∩C=∅时,(A-B)∪(A-C)=A。(2)由(1)可知:
(A-B)∪(A-C)=∅
<=> A-(B∩C) = ∅
<=> A⊆(B∩C)
因此,充要条件为 A⊆(B∩C)