今年较火的扩散模型Diffusion Model

🚀 作者 ：“码上有钱”
🚀 文章简介 ：AI-扩散算法
🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬

项目

扩散模型加噪去噪过程

原理

高斯噪声

在深度学习中，高斯噪声通常指的是一种服从高斯分布（正态分布）的随机噪声。它可以用来模拟真实世界数据中的噪声，并用于数据增强、数据生成和对抗训练等任务中。

在深度学习中，高斯噪声通常被添加到输入数据中，以模拟真实世界中存在的噪声。例如，在图像分类任务中，为了增强模型的鲁棒性，可以给输入图片添加高斯噪声，并通过训练使网络能够去除这些噪声而正确分类图像。又比如，在生成对抗网络（GAN）中，生成器网络在生成图片时，也会利用高斯噪声来增加图片的多样性和真实感。

高斯噪声的形式可以表示如下：

$\sigma * N(0, 1) + \mu$

其中， $N (0, 1)$ 表示均值为0，方差为1的标准正态分布。 $\sigma$ 控制噪声的幅度， $\mu$ 表示噪声的均值。

在深度学习中，我们可以将高斯噪声加到输入数据上，也可以将其加到网络参数上。具体来说，当将高斯噪声添加到输入数据时，我们可以将噪声视为一种正则化机制，它有助于减小模型对输入的过拟合。而当将高斯噪声添加到网络参数时，我们可以将噪声视为随机搜索的一种策略，帮助模型在训练过程中跳出局部极小值。

具体应用中，我们常使用均值为0、标准差为1的标准正态分布生成随机数作为噪声
$\epsilon \sim N(0, 1)$

然后通过一个线性变换使得其满足我们要求的分布形状。这样生成的高斯噪声可以用来增强输入数据或者是网络参数。

扩散现象

在数学和物理学中，扩散是指粒子从一个区域向其它区域的传递。这个过程可以描述为一个颗粒从初始位置开始随机移动，直到某个时刻停止。在此过程中，粒子以很高速度在一个方向上移动并与其他粒子发生碰撞，最终达到平衡状态。

在自然界中，扩散是一种非常普遍的现象，比如风经过树叶的摩擦会造成树叶的运动，污染物在空气中的传播也可以用扩散模型来解释。

在化学反应中，扩散是指物质由浓度较高的地方向浓度较低的地方传输。扩散是许多重要现象的基础，例如气体的扩散、电解质溶液的扩散等。
扩散现象

贝叶斯公式

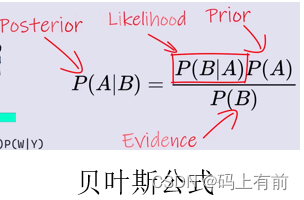
贝叶斯公式是应用在概率论和统计学中的。在机器学习中，我们经常使用贝叶斯公式来计算后验概率。

设有两个事件A和B，其中B不为0，则有
$\frac{P(B|A) \cdot P(A)}{P(B)}$

其中， $P (A ∣ B)$ 表示给定事件B发生的情况下，事件A发生的概率，称为后验概率。 $P (B ∣ A)$ 表示给定事件A发生的情况下，事件B发生的概率，称为似然度。 $P (A)$ 和 $P (B)$ 分别是事件A和B的边缘概率分布。

对于分类问题，我们假设输入样本 $x$ 属于类别 $C_{k}$ 的概率与日期 $t$ 无关；即 $P (y ∣ x, t) = P (y ∣ x)$ ， $y\in\{1,2.....K\}$ ， $t\in T$ ，其中 $T$ 是时间序列。

根据贝叶斯公式，后验概率可以表述如下：
\begin{equation}\label{eq:bayes}
P(y|x)=\frac{P(x|y)P(y)}{P(x)}
\end{equation}

假设存在一个集合 $T$ ，包含了一些期望的某一特性或性质。具体说来，对于每一个观察到的点 $x_t$ ，我们希望计算概率 $P(x_t|H)$ ，这里 $H$ 为假设。显然，在有限数据集的情况下，我们不能够取遍所有可能的 $H$ ，但是可以通过给定一些先验概率及常识假设来选择一个最可能的 $H$ 。接下来，我们通常通过最大化后验概率获得参数 $\theta_{\text{MAP}}^{(k)}$ 的推断。

$\theta_{\text{MAP}}^{(k)} = \argmax_{\theta_k}\left(P(\theta_k|D_1,..., D_n)=\frac{P(D_1, ..., D_n|\theta_k)P(\theta_k)}{P(D_1, ..., D_n)}\right)$

最大似然法与期望极大算法

在实际应用中，最小化损失函数的过程往往比较复杂，缺乏闭式解。一个替代方案是使用贝叶斯公式定义的误差函数。它被称为对数损失函数（log loss function），或交叉熵损失函数（cross-entropy loss function）。对于二分类问题，可以使用如下形式来定义：
$f(\mathbf{x})) = -(y\log{\hat{y}} + (1 - y)\log{(1 - \hat{y})})$
其中 $y$ 为样本的真实类别， $\hat{y}$ 为模型预测的类别。对于多分类问题，可以应用softmax函数，将其转化为一系列二分类问题：
$f(\mathbf{x})) = -\sum_{c \in C} y_c \log{\hat{y}_c}$
其中 $C$ 表示所有可能的类别。

在求解最优参数时，我们通常不会直接使用这些损失函数，而是使用它们的平均值或者总和。例如，给定训练样本 $x_1, y_1)$ 、 $x_2, y_2)$ 、…、 $x_n, y_n)$ ，我们要试图最小化下式：

$\frac{1}{n}\sum_{i=1}^n L(y_i, f(x_i))$

其中 $L(y_i, f(x_i))$ 是针对每个样本点的“损失（loss）”函数， $n$ 是样本数

神经网络中的梯度下降

当模型不断调整时，损失函数也在变化，我们需要找到一个方法来计算目标函数的导数，以便能够确定是否达到了最佳状态或者最低点。Stanford大学的教授Andrew Ng曾经描述过使用梯度下降算法寻找函数最小值的方法：

随机初始化参数 $W_1,b_1,W_2,b_2$ 。
不断重复以下操作，直至满足停止条件：
- 计算损失函数关于参数的梯度。
- 更新参数 $W_1,b_1,W_2,b_2$ 。

这一方法被称为“随机梯度下降（Stochastic Gradient Descent）”。在每次安装数据计算梯度时，我们从训练集中随机选择一个样本，并基于此样本来进行梯度更新。这种方法之所以起作用是因为它使用了足够大的训练集，足够小的学习率和足够的迭代次数，使得最终的模型达到收敛。

对于正则化，对于L2范数惩罚而言，有可微的简化公式：
$\frac{\partial}{\partial w}(1/2\parallel w \parallel_{2}^{2}) = w$

对于L1范数惩罚而言，则有：
$\frac{\partial}{\partial w}(\parallel w \parallel_{1}) = sgn(w)$

对于整个目标函数，最后的形式是：
$J(\theta)=\sum_{i=1}^{m}( y^{(i)}log(h_{\theta}(x^{(i)})) + (1 - y^{(i)})log(1 - h_{\theta}(x^{(i)}))) + \frac{\lambda}{2}\sum_{j=1}^{n}w_j^2$

逻辑回归损失函数的导数

根据逻辑回归函数的定义：
$\begin{aligned} h_{\theta}(x^{(i)}) &= g(\theta^T x^{(i)}) \\ g(z)& = \frac{1}{1+e^{-z}} \end{aligned}$

我们接下来计算 $\delta$ 代表误差值:
$\delta = -\frac{\partial}{\partial z} \sum_{i=1}^{m}( y^{(i)}log(h_{\theta}(x^{(i)})) + (1 - y^{(i)})log(1 - h_{\theta}(x^{(i)})))$

对 $\delta$ 做一些变换就可以得到：
$\delta = -\sum_{i=1}^{m}(y^{(i)} - h_{\theta}(x^{(i)})) = (\hat{y} - Y)$

即误差项为： $\hat{y} - Y$

对于上述公式，我们可以发现 $P (Y = y ∣ X)$ 可以解出：
$y_i | X) = \frac{\exp^{(W \cdot x)}}{\sum_{j=1}^{k}\exp^{(W_j \cdot x)}}$

用代码实现如下：

class LogisticRegression:

    def __init__(self, learning_rate=0.1, iterations=100):
        self.learning_rate = learning_rate #learning rate
        self.iterations = iterations #num of iterations in GD
    
    def fit(self, X, y):
        self.X_train = X
        self.y_train = y
        self.n_samples, self.n_features = X.shape
        self.W = np.zeros(self.n_features + 1)   #Add 1 to the shape for bias term
        self.costs = []
        X = np.column_stack((np.ones((self.n_samples,1)), X))
        m = self.n_samples

        for i in range(self.iterations):
            h = self.sigmoid(np.dot(X, self.W)) 
            self.grad =(1 / m) * X.T @ (h - y)
            self.W -= self.learning_rate * self.grad
            if i % 100 == 0:
                cost = self.cost_function(X, y)
                self.costs.append(cost)
                print(f"Cost at iteration {i}", cost)

    def sigmoid(self, z):
        return 1 / (1 + np.exp(-z))

    def cost_function(self, X, y):
        h = self.sigmoid(np.dot(X, self.W))
        epsilon = 1e-5
        errors = y*np.log(h+epsilon) + (1-y)*np.log(1-h+epsilon)
        J = - np.sum(errors)
        return J

    def predict_proba(self, X):
        X = np.column_stack((np.ones((X.shape[0],1)), X))
        return self.sigmoid(np.dot(X,self.W))

    def predict(self, X, threshold=0.5):
        X = np.column_stack((np.ones((X.shape[0],1)), X))
        return self.predict_proba(X) >= threshold
 
    def score

过程

扩散模型过程

前向加噪

图像有三个通道的RGB颜色组成，同时我们生成一个服从正太分布的高斯噪声，通过归一化将其放缩到[-1, 1]上，通过下面这个公式进行计算加噪后的新图像，这里面的β表示扩散快慢的程度，越大表示扩散越快。
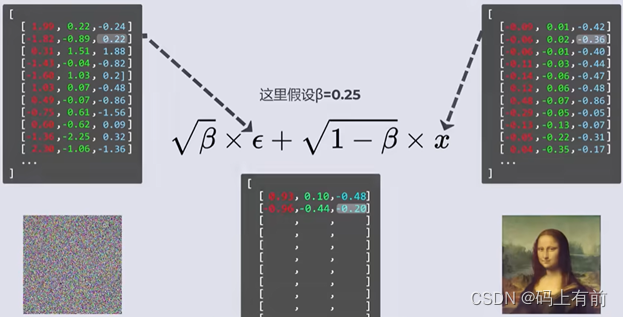
在这里插入图片描述
通过逐步加噪最终将图像变得完全模糊，在不断的迭代下逐渐模糊，但是发现一个问题，只能获得下一时刻加噪的图像。

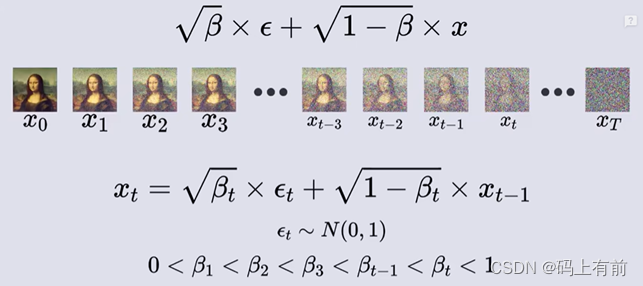
因此我们将1式代入2式再代入3式

令β = 1-α 可以得到一个t-2到t时刻的通式

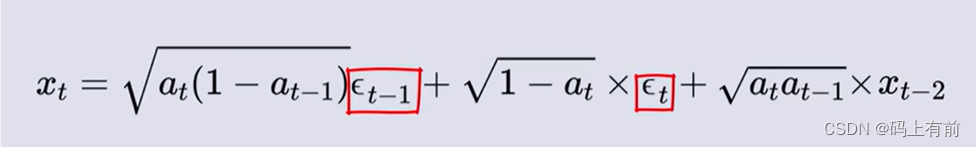
我们计算出上述标红所服从的概率，再通过重参数化技巧将其转化
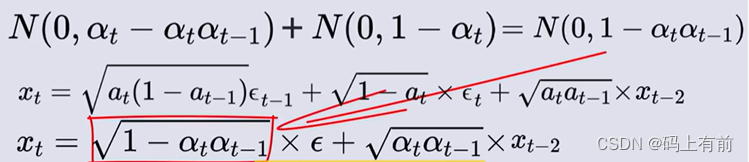
在这里插入图片描述
通过数学归纳法，就可以算出0时刻到任意t时刻的通式了

化简，令根号下多个α连乘为α拔，得到下面式子

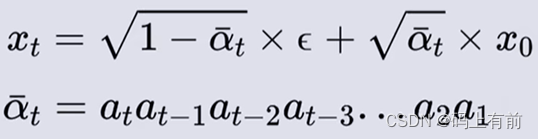
逆向去噪

逆向去噪是已知T时刻图像而求前一图像的过程，因此我们使用贝叶斯公式
在这里插入图片描述
同样我们计算出右式中每个概率服从的概率密度，然后写出写出他们的概率密度函数代入到式中

代入右式

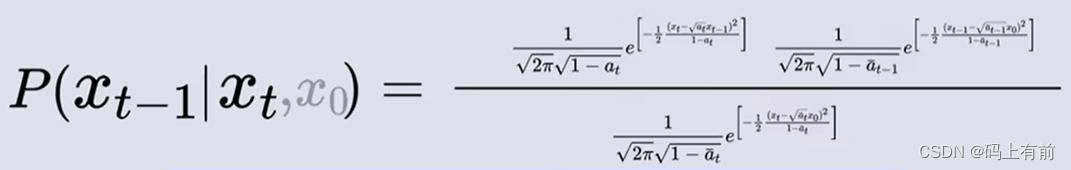
通过概率密度函数我们化简得到这个概率服从的概率密度

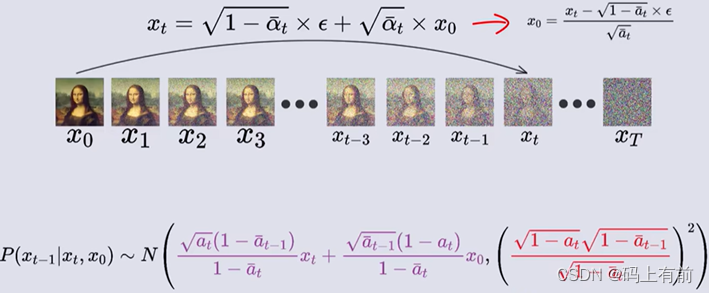
发现其中我们已知t时刻时求前一时刻的概率出现了0时刻的图像，但是我们又不知道0时刻的，陷入了死循环，这时我们将加噪过程中t时刻与0时刻的通式关系代入，化简，得到已知t时刻得到前一时刻图像服从的概率
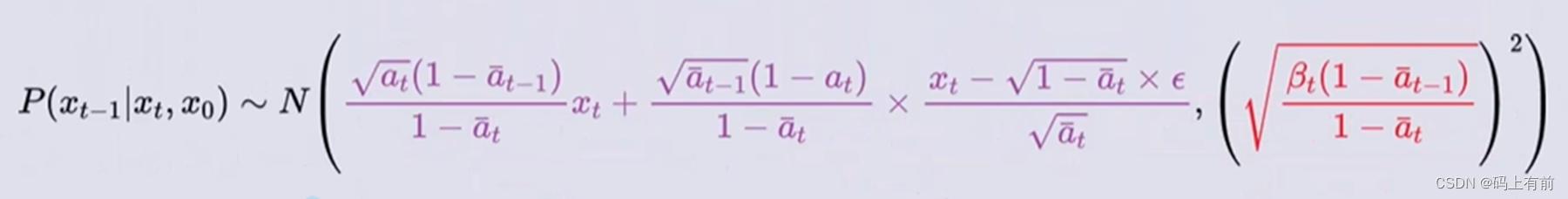
在这里插入图片描述
经过神经网络得到噪声的概率分布，经过随机采样得到t-1时刻的图像，经过不断迭代最终得到0时刻的图像，这就是整个过程，我们可以看到最后的α拔几乎为0，那么就得到t时刻的图像就为噪声了，服从标准正太分布。
在这里插入图片描述