垃圾插头DP，照着打都调了我一下午，淦！！！

学这个玩意纯粹是因为模拟赛考了一道，要不然碰都不会碰……

我觉得插头DP的主要难度在于实现，而不是理解算法原理……

不说废话了，进入正题。

解决的问题

学一个新知识点，肯定先要了解这个知识点能够解决什么样的问题。（废话）

其实插头DP就是一类特殊的状压DP，他解决的就是在小数据规模下连通性的问题，数据太大插头DP也不好做，毕竟本质还是状压。

举几个简单的例子，就比如说格点图的哈密顿路径计数，求棋盘的黑白染色方案满足相同颜色之间形成一个连通块的方案数，以及特定图的生成树计数等等，这些你看起来连暴力都不是很好搞的东西，插头DP就可以做。（说实话，就这复杂度，说暴力都有人信）

接下来我们先来了解几个概念。

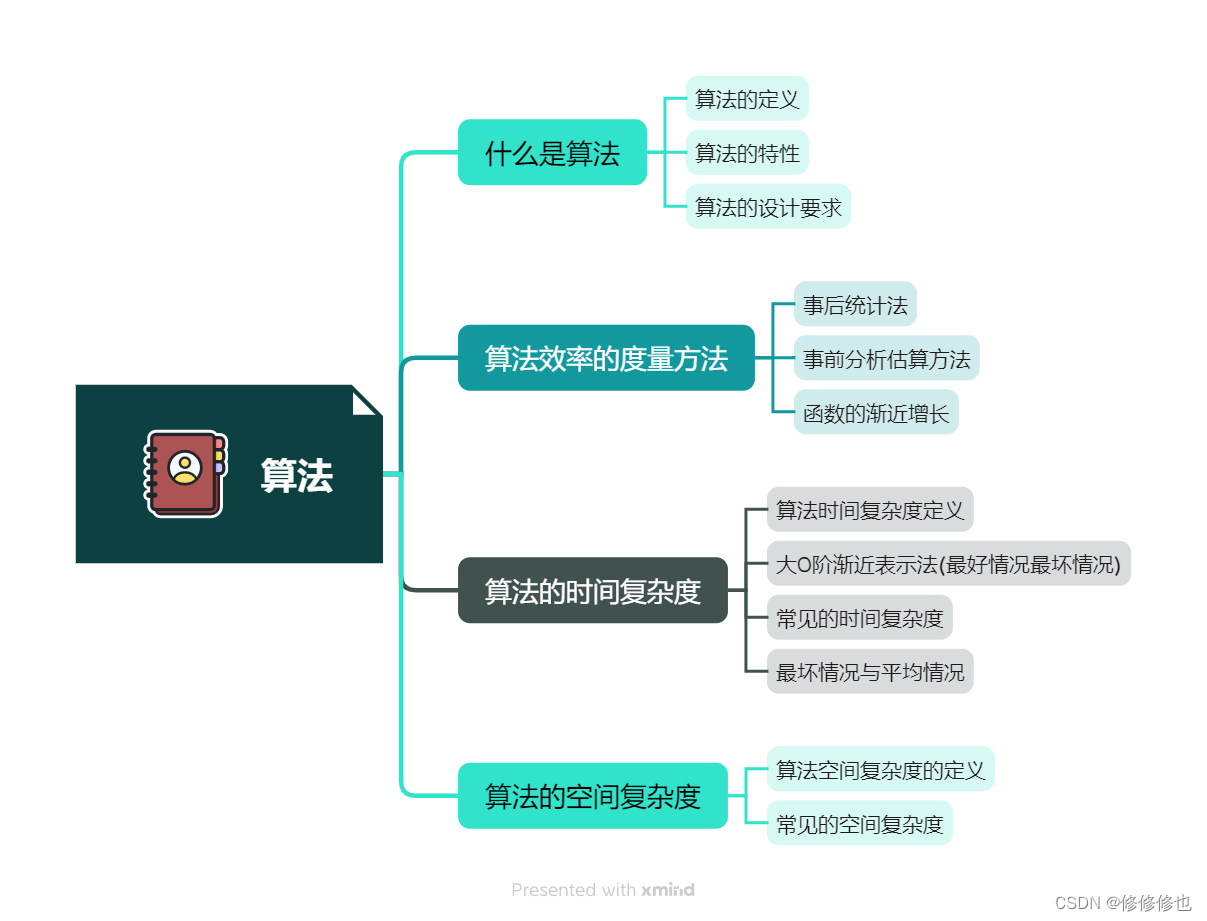
基本概念

---

插头

如果一个格子某个方向有插头，表示这个格子在这个方向与相邻格子是相连的。

简单点来说就是记录当前格子与相邻的格子是否连通。

轮廓线

就是已决策格子与未决策格子的分界线。（下图红色的线）

注意一下，这里分界线的边数是列数加一，别搞错了。

---

大概就这两个概念，我们现在来看看插头DP如何实现

实现

我们就借一道板题来说。

Luogu P5056 【模板】插头DP

因为数据较小，但是搜索过不了，于是考虑状压。（即插头DP）

可以逐格DP（某些题目可以逐行），设 $f_{i,j,state}$ 表示当前的方案数。

通常的 $state$ 有括号表示和最小表示，这里着重介绍泛用性更好的最小表示。我们用长度为 $m+1$ 的整形数组，记录轮廓线上每个插头的状态， $0$ 表示没有插头，并约定连通的插头用相同的数字进行标记。

由于要形成最小回路，可知最多只有两个插头互相连通，并且跟两组连通的插头之间不会交叉，既不会出现 $2121$ 的情况，并且每一个格子最多只有两个插头。

考虑如何转移。

对于上图黄色的格子，轮廓线为红色， 蓝色使我们DP完当前节点后的轮廓线（包括第一、二、四列的红线），我们分以下几种情况考虑。

• 跟上面和左边的格子都有插头，此时还要分两种情况。
  • 如果这两个插头没连通，则这个格子则不能有右插头和下插头，即新的两边轮廓线上没有任何插头。
  • 如果这两个插头连通了，若当前枚举的格子为最后一个格子，则直接连通，否则不能连通。（若连通则成为多个闭合回路了）
• 跟上面和左边的格子有一个插头，则此时跟下面和右边任意一个格子也有一个插头。
• 上面和左边都没有插头，则此时右边和下面都必须有插头。

注意考虑一下边界和障碍的条件。

当我们DP完一行时，轮廓线会变为下图形式：

此时我们在DP下一行之前记得将整个状态左移即可。

优化

对于普通的插头DP，时空复杂度也并不是非常优，此时就需要一点优化。

我们会发现由于他是闭合回路，它的状态会非常稀疏，于是我们可以用 hash 来优化。

但这个 hash 要用挂表法，即将你所有模数为 $x$ 的状态都挂到一起，可以用链式前向星维护。

你每次遇到一个新状态就将它存到哈希里面，然后查找状态则将那一条 hash 链枚举一遍即可。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200005, P = 9973, offset = 4, mask = (1 << offset) - 1;
int n, m, mp[20][20], ex, ey;
LL Val;
int in() {
    char ch = getchar();
    while (ch != '.' && ch != '*')
        ch = getchar();
    return ch == '*';
}
struct HashTable {//hash的实现
    int last[P], next[N], cnt;
    LL ans[N], state[N];
    void clear() {
        cnt = 0;
        memset(last, 0, sizeof(last));
    }
    void push(LL s) {
        LL x = s % P;
        for (int i = last[x]; i; i = next[i])
            if (state[i] == s) {
                ans[i] += Val;
                return ;
            }
        cnt++, state[cnt] = s, ans[cnt] = Val;
        next[cnt] = last[x], last[x] = cnt;
    }
    void roll() {
        for (int i = 1; i <= cnt; i++)
            state[i] = state[i] << offset;
    }
} H[2], *H0, *H1;
int bb[25], b[25];
LL encode() {//这是将数组加码成状态
    LL s = 0;
    memset(bb, -1, sizeof(bb));
    int bn = 1;
    bb[0] = 0;
    for (int i = m + 1; i; i--) {
        if (!~bb[b[i]])
            bb[b[i]] = bn++;
        s <<= offset;
        s |= bb[b[i]];
    }
    return s;
}
void decode(LL s) {//这是将状态解码成数组
    for (int i = 1; i <= m + 1; i++) {
        b[i] = s & mask;
        s >>= offset;
    }
}
void push(int j, int down, int right) {//将状态改变，然后往下DP
    b[j] = down, b[j + 1] = right;
    H1 -> push(encode());
}
void PlugDP() {//DP
    H0 = H, H1 = H + 1;
    H1 -> clear(), Val = 1, H1 -> push(0);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            swap(H0, H1), H1 -> clear();
            for (int l = 1; l <= (H0 -> cnt); l++) {
                decode(H0 -> state[l]);
                Val = H0 -> ans[l];
                int left = b[j], up = b[j + 1];
                //上面和左边的插头类型
                bool down = i != n, right = j != m;;
                //这两个变量即是判断是否处于边界位置，能否有右插头和下插头
                if (mp[i][j] == 1) {//如果当前格子为障碍
                    if (!left && !up) {//如果上面和左边都没有插头，则可以转移成下面和右边也都没有插头
                        push(j, 0, 0);
                    }
                }
                else if (left && up) {//上面和左边都有插头
                    if (left == up) {//两个插头连通
                        if (i == ex && j == ey)
                            push(j, 0, 0);
                    }
                    else {//两个插头不连通
                        for (int t = 1; t <= m + 1; t++)
                            if (b[t] == left)
                                b[t] = up;
                        push(j, 0, 0);
                    }
                }
                else if (left || up) {//上面和左边只有一个插头
                    int t = left | up;
                    if (down)
                        push(j, t, 0);
                    if (right)
                        push(j, 0, t);
                }
                else if (down && right)//两边都没有插头并且下面和右边都可以有插头
                    push(j, m, m);
            }
        }
        H1 -> roll();//即全部右移
    }
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) {
            mp[i][j] = in();
            if (!mp[i][j])
                ex = i, ey = j;
        }
    PlugDP();
    cout << (H1 -> cnt == 1 ? H1 -> ans[1] : 0) << endl;
    return 0;
}