高斯消元法的基本原理是通过一系列行变换将线性方程组的增广矩阵转化为简化行阶梯形式,从而得到方程组的解。其核心思想是利用矩阵的行变换操作,逐步消除未知数的系数,使得方程组的求解变得更加简单。
首先,给定系数矩阵A和常数向量b,将它们合并为增广矩阵a。然后确定增广矩阵的行数n和列数m。
接下来,使用两个嵌套的循环,依次进行消元计算。外层循环i从1到n遍历每一行,内层循环j从m递减到i遍历当前行的每个元素。在每次循环中,将当前行的第j个元素除以第i个元素,即将主元归一化为1。
然后,通过两个嵌套的循环,对i+1到n的行进行消元计算。内层循环k从m递减到i遍历当前行的每个元素,将当前行的第k个元素减去第j行的第i个元素乘以第i行的第k个元素,即利用消元操作将当前列的下面各行的对应元素都消为0。
然后,使用一个逆序的循环,从第n-1行开始回代求解未知数。在每次循环中,内层循环j从i递减到1,将当前行的最后一个元素减去第i+1行的第m个元素乘以第j行的第m个元素,即通过回代操作求解未知数。
实际上就是两个三层循环,消元一个三层循环和回代一个三层循环,即算法的复杂度为O(n3)。
A=[1,1,2,1;1,2,0,1;1,4,2,1;1,8,2,4];
b=[2;0;2;3];
A_b=[A,b];
[n,m]=size(A_b);
for i=1:n
for j=m:-1:i
A_b(i,j)=A_b(i,j)/A_b(i,i);
end
for j=i+1:n
for k=m:-1:i
A_b(j,k)=A_b(j,k)-A_b(j,i)*A_b(i,k);
end
end
fprintf('第%d次消元\n',i);
disp(rats(A_b));
end
for i=n-1:-1:1
for j=i:-1:1
A_b(j,m)=A_b(j,m)-A_b(j,i+1)*A_b(i+1,m);
A_b(j,i+1)=0;
end
fprintf('第%d次回代\n',n-i);
disp(rats(A_b));
end
在高斯消去法中,如果一个列中的主元很小,那么在后续的计算过程中,将会产生较大的误差。这是因为在消元过程中,除法运算会引入数值误差,而被除数过小可能导致舍入误差放大。
通过进行列主元选取,即选择当前列中绝对值最大的元素所在的行作为主元行,可以有效地避免除数过小的情况。选择绝对值最大的元素作为主元,能够减小舍入误差的累积,从而提高计算过程的稳定性。它可以减少舍入误差对计算结果的影响,保证所得到的解更加精确和可靠。
% A=[1,1,2,1;1,2,0,1;1,4,2,1;1,8,2,4];
% B=[0.0001,1,2,1;1,2,0,1;1,4,2,1;1,8,2,0.0004];
% b=[2;0;2;3];
A_b=[A,b];
[n,m]=size(A_b);
for i=1:n
[~,maxIndex]=max(abs(A_b(i:n,i:i)));
maxIndex=i+maxIndex-1;
if i~=maxIndex
A_b([i,maxIndex],:)=A_b([maxIndex,i],:);
end
for j=m:-1:i
A_b(i,j)=A_b(i,j)/A_b(i,i);
end
for j=i+1:n
for k=m:-1:i
A_b(j,k)=A_b(j,k)-A_b(j,i)*A_b(i,k);
end
end
fprintf('第%d次消元\n',i);
disp(rats(A_b));
end
for i=n-1:-1:1
for j=i:-1:1
A_b(j,m)=A_b(j,m)-A_b(j,i+1)*A_b(i+1,m);
A_b(j,i+1)=0;
end
fprintf('第%d次回代\n',n-i);
disp(rats(A_b));
end
x=A_b(:,end:end);
fprintf('高斯列主元消去法\n');
disp(rats(x));
fprintf('matlab内置函数求逆求解\n');
xx=A^(-1)*b;
disp(rats(xx));
diff=x-xx;
stem(1:100,diff);与matlab内置求逆的解相比 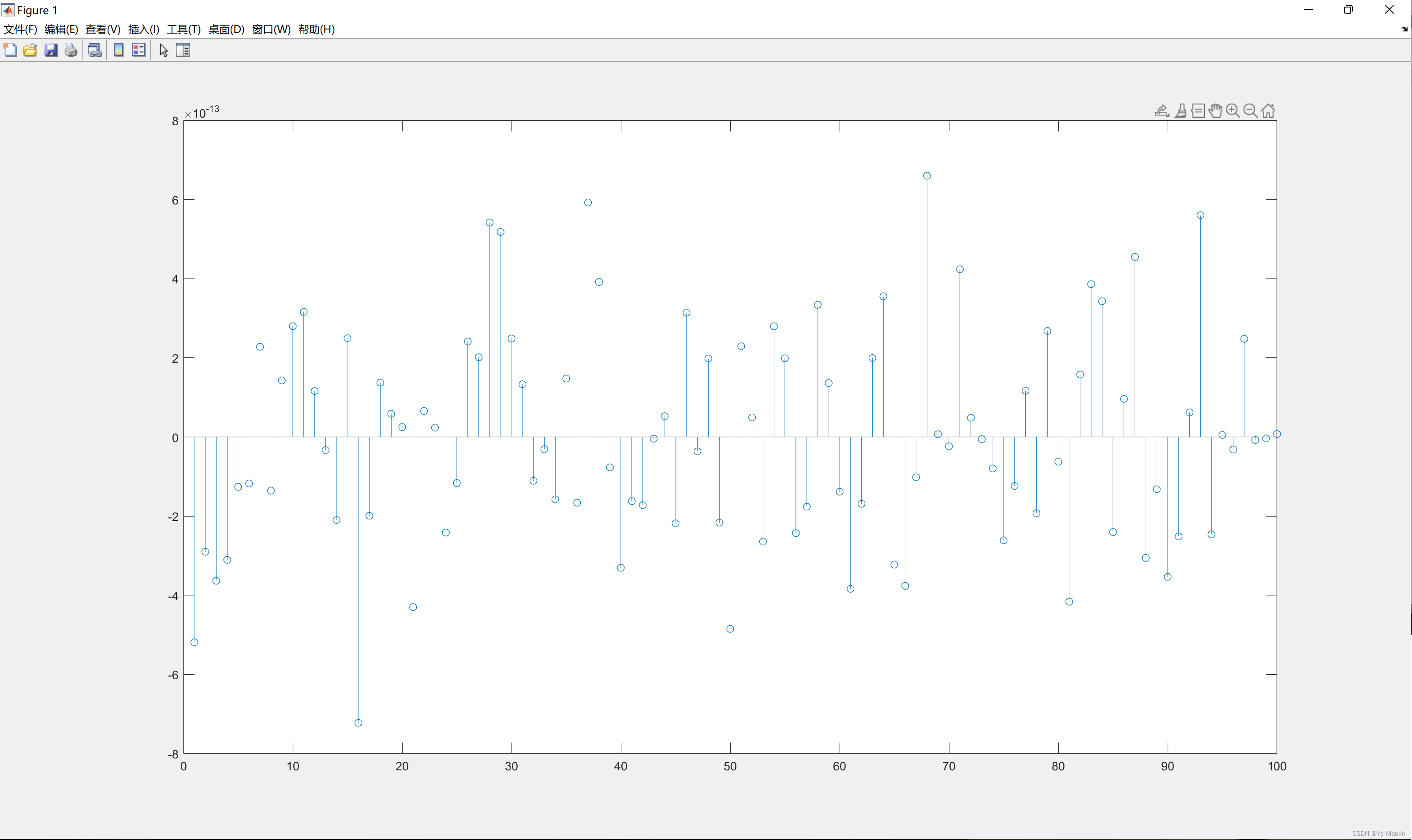





![[鹏城杯 2022]简单的php - 无数字字母RCE+取反【*】](https://img-blog.csdnimg.cn/f86d1776abe04b54a02d7d21e9fd56e2.png)