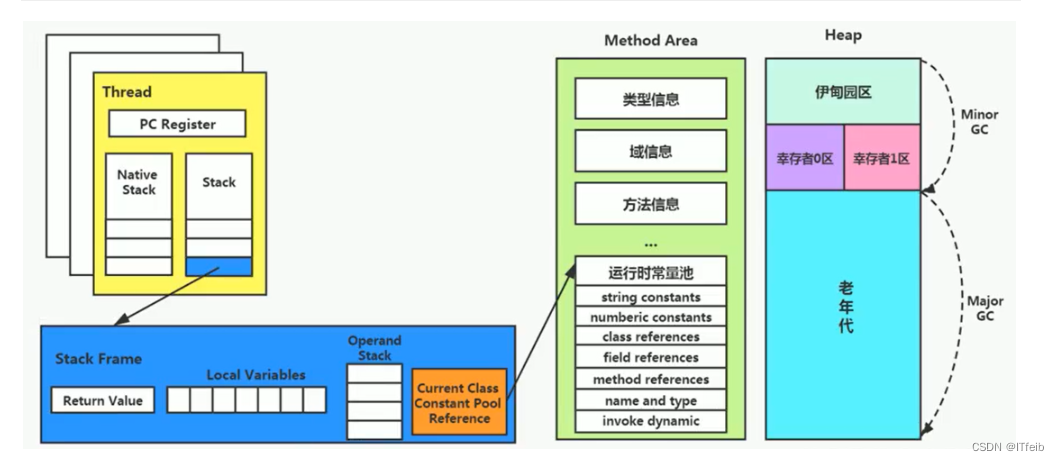
Description
一个无限行的数字三角形,第 i 行有 i 个数。第一行的第一个数是 1 ,其他的数满足如下关系:如果用 F[i][j] 表示第 i 行的第 j 个数,那么 F[i][j]=A∗F[i−1][j]+B∗F[i−1][j−1] (不合法的下标的数为 0 )。 当 A=2,B=3 时的数字三角形的前 5 行为: 1 2 3 4 12 9 8 36 54 27 16 96 216 216 81 现在有 T 次询问,求 A=a,B=b 时数字三角形的第 n 行第 m 个数的值模 10^9+9 的结果。
Input
第一行为一个整数 T 。 接下一共 T 行,每行四个整数 a,b,n,m
Output
一共 T 行,每行一个整数,表示那个位置上的数的值。
Sample Input
2 2 3 3 3 3 1 4 1
Sample Output
9 27
Hint
n,t<=1e5;1<=m<=n; 0<=a,b<=1e9;
思路:
看例子:
1
A B
A^2 2*A*B B^2
A^3 3*A^2*B 3*A*B^2 B^3
我们可以看出答案是:
对于,分母我们利用费马小定理求逆元。
代码:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<unordered_map>
#include<map>
using namespace std;
#define LL long long
const long long mod = 1e9 + 9;
const int N = 1e5 + 100;
LL xia[N];
LL quick(LL a, LL b, LL p)//根据a^(p-1)%p=1求a的逆元a^(p-2)%p;
{
LL res = 1;
while (b)
{
if (b & 1) res = (res * a) % p;
b >>= 1;
a = (a * a) % p;
}
return res;
}
LL seek(LL x, LL y)
{
LL e = 1;
while (y)
{
if (y & 1)
e = e * x % mod;
x = x * x % mod;
y = y >> 1;
}
return e;
}
int main()
{
int T;
LL a, b, n, m;
xia[0] = 1;
for (int i = 1; i <=1e5; i++)
xia[i] = (xia[i-1] * i) % mod;
scanf("%d", &T);
while (T--)
{
LL ans = 1;
scanf("%lld%lld%lld%lld", &a, &b, &n, &m);
ans = (ans*seek(a, n - m))%mod;
ans = (ans*seek(b, m-1))%mod;
ans = (ans * xia[n-1]) % mod;
ans = (ans * quick(xia[m-1], mod - 2, mod)) % mod;
ans= (ans * quick(xia[n-m], mod - 2, mod)) % mod;
printf("%lld\n",(ans % mod + mod) % mod);
}
return 0;
}