http://cplusoj.com/d/senior/p/SS231007D

分析题目性质，有：

1. 按编号顺序最短路必然为连续段
2. 边只会在连续段内和相邻连续段之间连
3. $i$ 段 连 $i+1$ 段，$i+1$ 段中每个点恰有1条来自 $i$ 的边

然后肯定是考虑 $f(l,r)$ 表示最后一段为 $[l,r]$ 的答案，考虑由 $f(k,l-1)$ 转移

我们可以求出 $[k,l-1]$ 中有多少个3度点，多少个2度点。然后记 $g(i,x,y)$ 表示下一层有 $i$ 个点，这层有 $x$ 个2，$y$ 个3度点的方案数。可以用类似递归的方法来推：

$g(i,x,y)=x\times g(i-1,x-1,y)+y\times g(i-1,x+1,y-1)$，也就是考虑最后一个点用2度点还是3度点

所以就有 $f(l,r)={\sum }_{k<l}f(k,l-1)g(r-l+1,S2(k,l-1),S3(k,l-1))$
。
我们刚刚计算 $g$ 是只考虑块直接的贡献，我们现在要考虑块内的贡献，我们可以计算到 $g(0,x,y)$ 里。如果只考虑块内，每个点只能为1度或2度点。我们发现只能长成这个形式：

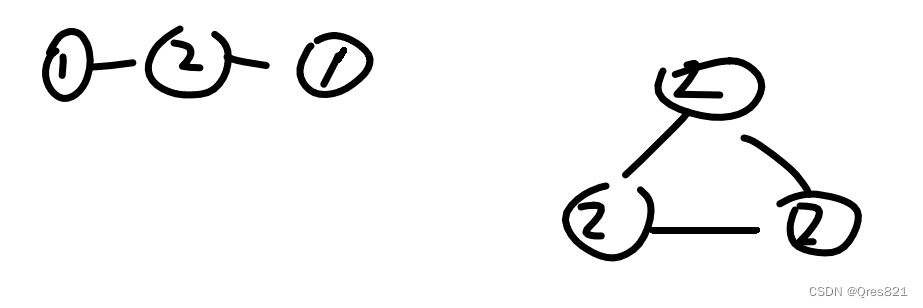
我们可以分块统计，枚举多少个2成环，记为 $h_i$。我们可以枚举最后一个点所在环的大小，然后乘上一个圆排列。
$h_i=\sum h_j\frac{(i-j-1)!}{2}\left(\genfrac{}{}{0ex}{}{i-1}{j}\right)$

首先对1要量量匹配，方案有 $\frac{x!}{\frac{x}{2}!2^{\frac{x}{2}}}$。然后剩下的2直接插板。也就是 $g_{0,x,y}={\sum }_{i=0}^y\frac{x!}{\frac{x}{2}!2^{\frac{x}{2}}}\left(\genfrac{}{}{0ex}{}{y}{i}\right)h_i\left(\genfrac{}{}{0ex}{}{y-i+\frac{x}{2}-1}{\frac{x}{2}-1}\right)$

然后往前套即可。

最后一段不会向后连边，所以

$ans={\sum }_{i=1}{f}_{i,n}{g}_{0,s2[i:n],s3[1:n]}$

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//#define M
#define mo (int)(1e9+7)
#define N 310
int pw(int a, int b) {
	int ans=1; 
	while(b) {
		if(b&1) ans*=a; 
		a*=a; b>>=1; 
		ans%=mo; a%=mo; 
	}
	return ans; 
}
int fac[N<<2], inv[N<<2], ifac[N<<2]; 
void init(int n) {
	int i; 
	for(i=fac[0]=1; i<=n; ++i) fac[i]=fac[i-1]*i%mo; 
	ifac[n]=pw(fac[n], mo-2); 
	for(i=n-1; i>=0; --i) ifac[i]=ifac[i+1]*(i+1)%mo; 
    for(i=1; i<=n; ++i) inv[i]=ifac[i]*fac[i-1]%mo; 
}
int C(int n, int m) {
	if(m>n) return 0;
	return fac[n]*ifac[m]%mo*ifac[n-m]%mo; 
}
void Add(int &a, int b) {
	a+=b; if(a>=mo || a<=-mo) a%=mo; 
    if(a<0) a+=mo; 
}
const int iv2=pw(2, mo-2); 


int n, m, i, j, k, T;
int s1[N], s2[N], f[N][N], g[N][N][N], h[N], d[N], ans, l, r, x, y;  

int S1(int l, int r) {
	return s1[r]-s1[l-1]; 
}

int S2(int l, int r) {
	return s2[r]-s2[l-1]; 
}

signed main()
{
//	freopen("in.txt", "r", stdin);
//	freopen("out.txt", "w", stdout);
	freopen("graph.in", "r", stdin);
	freopen("graph.out", "w", stdout);
//	srand(time(NULL));
//	T=read();
//	while(T--) {
//
//	}
	n=read(); init(1200); 
	for(i=1; i<=n; ++i) d[i]=read()-1; ++d[1]; 
	for(i=1; i<=n; ++i) if(d[i]==2) ++s2[i]; else ++s1[i]; 
	partial_sum(s1+1, s1+n+1, s1+1); 
	partial_sum(s2+1, s2+n+1, s2+1); 
	h[0]=g[0][0][0]=1; 
	for(i=3; i<=n; ++i) {
		h[i]=fac[i-1]*iv2%mo; 
		for(j=3; j<=i-3; ++j)
			Add(h[i], h[j]*C(i-1, j)%mo*fac[i-j-1]%mo*iv2%mo); 
		g[0][0][i]=h[i]; 
//		printf("h[%lld]=%lld\n", i, h[i]); 
	}
	for(x=2; x<=n; x+=2) 
		for(y=0; y<=n; ++y) {
			k=fac[x]*ifac[x/2]%mo*pw(pw(2, x/2)%mo, mo-2)%mo; 
			for(i=0; i<=y; ++i) {
				Add(g[0][x][y], k*h[i]%mo*C(y, i)%mo*C(y-i+x/2-1, x/2-1)%mo*fac[y-i]%mo); 
//				if(x==4 && y==10) printf("%lld %lld %lld %lld %lld\n", h[i], C(y, i), )
			}
				
//			printf("g [ 0 %lld %lld ] =%lld %lld\n", x, y, g[0][x][y], k); 
		}
	for(i=1; i<=n; ++i) 
		for(x=0; x<=n; ++x) 
			for(y=0; y<=n; ++y) {
				if(x) Add(g[i][x][y], x*g[i-1][x-1][y]%mo); 
				if(y) Add(g[i][x][y], y*g[i-1][x+1][y-1]%mo); 
//				printf("g[%lld][%lld][%lld]=%lld\n", i, x, y, g[i][x][y]); 
			}
	f[2][d[1]+1]=1; 
	for(l=d[1]+2; l<=n; ++l) 
		for(r=l; r<=n; ++r) {
			for(k=1; k<l; ++k) {
				Add(f[l][r], f[k][l-1]*g[r-l+1][S1(k, l-1)][S2(k, l-1)]%mo); 
//				printf("f[%lld][%lld]=%lld %lld %lld(%lld %lld)\n", l, r, f[l][r], f[k][l-1],
//						 g[r-l+1][S1(k, l-1)][S2(k, l-1)], S1(k, l-1), S2(k, l-1)); 
			}
//				printf("f[%lld][%lld]=%lld\n", l, r, f[l][r]); 
		}
	for(i=1; i<=n; ++i) {
		Add(ans, f[i][n]*g[0][S1(i, n)][S2(i, n)]%mo); 
//		printf("[%lld %lld] %lld %lld %lld %lld\n", i, n, f[i][n], S1(i, n), S2(i, n), g[0][S1(i, n)][S2(i, n)]); 
	}
	printf("%lld", (ans%mo+mo)%mo); 
	return 0;
}