文章目录
- 前言
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
前言
本专栏文章为《代码随想录》书籍的刷题题解以及读书笔记,如有侵权,立即删除。
一、题目
1、原题链接
209. 长度最小的子数组
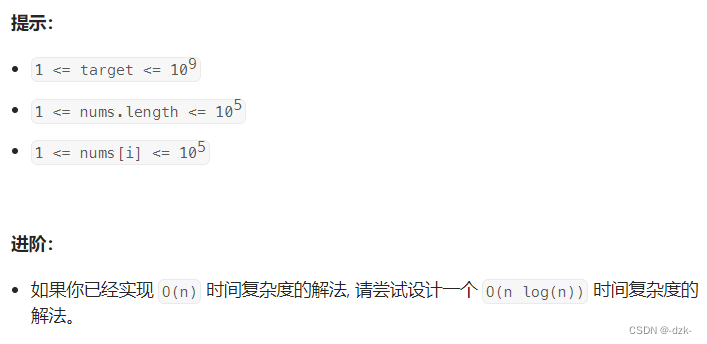
2、题目描述
二、解题报告
1、思路分析
- 暴力解法
利用两层循环,第一层循环枚举子数组的起点位置,第二层循环枚举子数组的终点位置,第二层循环中可以同时来统计当前子数组的和,如果符合题目条件则更新length,否则继续循环,直至两层循环结束,返回题目要求的值,算法结束。 - 滑动窗口
利用两个指针,i指向窗口起始位置,j指向窗口的终止位置。初始时i和j均指向数组中第一个元素,指针j不断向后遍历,当区间[i,j]中数组元素和大于等于target时(只要满足这个条件就执行后面操作,即为while循环),根据当前子数组的长度来确定是否更新length,向后移动i指针(原因:因为区间[i,j]中的元素和已经大于等于target,如果此时i指针不动,j指针继续向后遍历,之后的区间一定满足元素和大于等于target,但是数组长度一定不比当前[i,j]区间的长度短,即此时i指针不动,j向后遍历到的各个位置与i组成的区间[i,j]一定不是答案,所以此时已经没有必要让i再待在当前位置了,故需要移动i到下一个位置),直至j遍历完所有位置,返回题目要求的值,算法结束。
2、时间复杂度
暴力解法时间复杂度O(n^2)
滑动窗口时间复杂度O(n)
3、代码详解
暴力解法代码(TLE、力扣无法AC)
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
//将长度初始化为整型最大值
int length = INT_MAX;
for (int i = 0; i < nums.size(); i++) {
int sum = 0;
for (int j = i; j < nums.size(); j++) {
sum += nums[j];
//j-i+1表示当前满足条件的数组长度
if (sum >= target && j - i + 1 < length) {
length = j - i + 1;
}
}
}
//如果length没有被更新说明不存在符合条件的子数组
return length == INT_MAX ? 0 : length;
}
};
滑动窗口代码
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int length = INT_MAX;
//nowLength记录当前符合条件的子数组长度
int nowLength = 0;
//sum记录当前子数组的元素之和
int sum = 0;
int i = 0;
for (int j = 0; j < nums.size(); j++) {
sum += nums[j];
while (sum >= target) {
nowLength = j - i + 1;
length = length > nowLength ? nowLength : length;
//窗口缩小:因为当前[i,j]之间已经是最优答案,没有再以i开头的区间比当前结果更优
sum -= nums[i++];
}
}
return length == INT_MAX ? 0 : length;
}
};
三、知识风暴
INT_MAX或INT32_MAX表示整型的最大值- 滑动窗口