一、简介
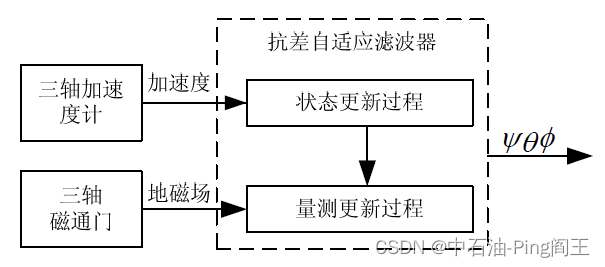
抗差自适应滤波:利用等价权函数和自适应因子合理的分配信息,有效地滤除钻具振动对动态姿态测量的影响。、
针对导向钻井工具动态测量受钻具振动的影响而导致测量不准确的问题,提出一种抗差自适应滤波的动态空间姿态测量方法。通过分析钻具振动对姿态测量的影响,并吸收抗差估计和自适应滤波的优点,利用抗差等价权矩阵自适应的确定量测信息,通过自适应因子调整状态模型信息对状态参数的整体贡献,从而消除钻具振动对动态姿态测量的影响,获得实时性强、精度高的姿态参数,提高钻井效率,降低钻井风险。
在实际钻井过程中,钻头切削岩层、钻柱与井壁的碰撞等会使钻具产生横向振动、纵向振动和扭转振动等,这些振动严重的影响了测量传感器输出信号的正确性。
抗差自适应滤波的基本思想是:当观测值存在异常时,对观测值采用抗差估计原则,能够控制观测异常的影响;当动力学模型存在异常误差时,将动力学模型信息作为一个整体,采用统一的自适应因子调整动力学模型信息对状态参数的整体贡献。
二、测量系统建模
方位角
ψ
\psi
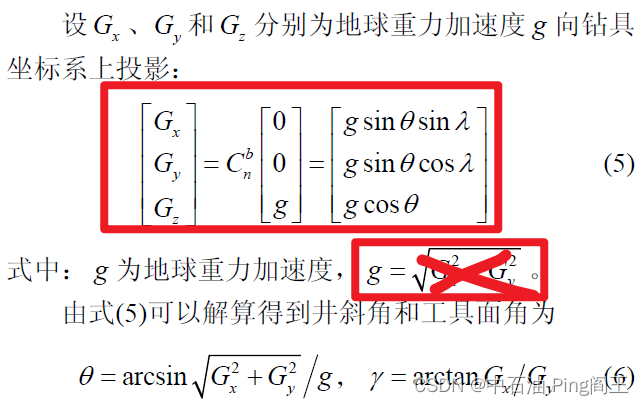
ψ为磁北方向沿逆时针方向到Z 轴在水平面的投影间的夹角,其范围在0°~360°之间,井斜角
θ
\theta
θ为钻进轴Z 轴与水平面所成的夹角,规定向下为正,反之为负,其范围为-90°~90°,工具面向角
γ
\gamma
γ 则为钻孔横截面内由钻孔高边到Y 轴所成的角度,范围在0°~360°之间。这样,我们就准确的定义了井下钻具的方位角
ψ
\psi
ψ 、井斜角
θ
\theta
θ 和工具面向角
γ
\gamma
γ ,且角度的正向都符合右手系原则。
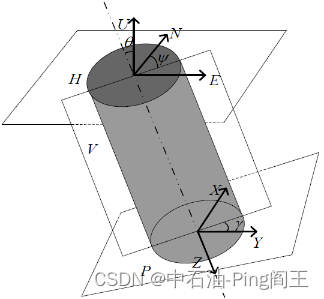
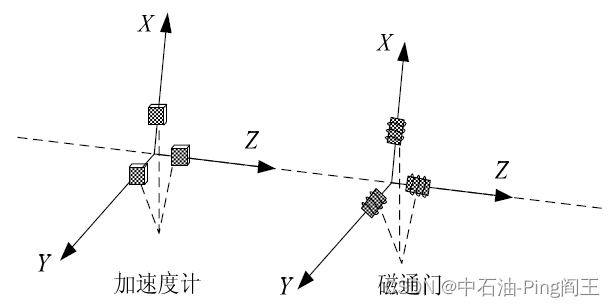
加速度计和磁通门安装如下:
根据上述理论,建立导向钻井工具姿态测量的动
态数学模型,给出状态方程和量测方程:
x
k
^
=
Φ
k
,
k
−
1
x
k
−
1
+
w
k
\hat{x_k} = \Phi_{k,k-1}x_{k-1}+w_{k}
xk^=Φk,k−1xk−1+wk
x
k
x_k
xk 和
x
k
−
1
x_{k-1}
xk−1分别为
t
k
t_k
tk 和
t
k
−
1
t_{k-1}
tk−1时刻的n 维状态参数向量,
Φ
k
,
k
−
1
\Phi_{k,k-1}
Φk,k−1为n× n维状态转移矩阵;
w
k
w_k
wk 为p 维动力学模型误差向量,其数学期望为0,协方差矩阵为:
∑
w
k
w
i
=
{
∑
w
k
,
k
=
i
0
,
k
≠
i
\sum_{wkwi}= \begin{cases}\sum_{wk},\quad &k=i\\0,\quad &k\neq i\end{cases}
wkwi∑={∑wk,0,k=ik=i
w
k
wk
wk为高斯白噪声序列。
设
t
k
t_k
tk时刻的量测方程为
y
k
=
H
k
x
k
+
v
k
y_k=H_kx_k+v_k
yk=Hkxk+vk
y
k
y_k
yk 为
t
k
t_k
tk时刻的m维观测向量;
H
k
H_k
Hk为m× n维测量矩阵,也称为观测矩阵;
v
k
v_k
vk为m维观测误差向量,其数学期望为0,协方差矩阵为
∑
v
k
v
i
=
{
∑
v
k
,
k
=
i
0
,
k
≠
i
\sum_{vkvi}= \begin{cases}\sum_{vk},\quad &k=i\\0,\quad &k\neq i\end{cases}
vkvi∑={∑vk,0,k=ik=i
v
k
v_k
vk为高斯白噪声序列。在
i
=
k
i=k
i=k时,
w
k
w_k
wk 和
v
k
v_k
vk的协方差矩阵分别为
∑
w
k
\sum_{wk}
∑wk和
∑
v
k
\sum_{vk}
∑vk,这里
w
k
w_k
wk,
w
i
w_i
wi,
w
k
w_k
wk,
v
i
v_i
vi互不相关。
状态向量为:
X
=
[
ψ
,
θ
,
γ
]
T
X=\begin{bmatrix}\psi,\theta,\gamma\end{bmatrix}^T
X=[ψ,θ,γ]T,表明直接将钻具姿态参数作为状态向量,而
非姿态误差作为状态。
三、动态姿态测量
X
‾
k
=
Φ
k
,
k
−
1
X
k
−
1
^
\overline{X}_{k} = \Phi_{k,k-1}\hat{X_{k-1}}
Xk=Φk,k−1Xk−1^为系统的状态预测方程。
X
‾
k
\overline{X}_{k}
Xk为
t
k
t_k
tk的状态预测方程,
X
k
−
1
^
\hat{X_{k-1}}
Xk−1^为
t
k
−
1
t_{k-1}
tk−1为状态估计向量。设状态预测向量
X
‾
k
\overline{X}_k
Xk的误差方程为:
V
X
‾
k
=
X
^
k
−
X
‾
k
=
X
^
k
−
Φ
k
,
k
−
1
X
^
k
−
1
V_{\overline{X}_k} = \hat{X}_k-\overline{X}_k=\hat{X}_k-\Phi_{k,k-1}\hat{X}_{k-1}
VXk=X^k−Xk=X^k−Φk,k−1X^k−1
V
X
‾
k
V_{\overline{X}_k}
VXk为
t
k
t_k
tk时刻状态预测向量
X
^
k
\hat{X}_k
X^k的残差向量。
残差向量和新息向量(也称为预测残差向量)分别为:
V
k
=
H
k
X
^
k
−
Y
k
V_k=H_k\hat{X}_k-Y_k
Vk=HkX^k−Yk
V
‾
k
=
H
k
X
‾
k
−
Y
k
\overline{V}_k=H_k\overline{X}_k-Y_k
Vk=HkXk−Yk
V
k
V_k
Vk和
V
‾
k
\overline{V}_k
Vk的协方差矩阵为:
∑
V
k
=
∑
k
−
H
k
∑
X
^
k
H
k
T
\sum_{V_k} = \sum_{k}-H_k\sum_{\hat{X}_k}H^T_k
Vk∑=k∑−HkX^k∑HkT
∑
V
‾
k
=
∑
k
+
H
k
∑
V
‾
k
H
k
T
\sum_{\overline{V}_k} = \sum_{k}+H_k\sum_{\overline{V}_k}H^T_k
Vk∑=k∑+HkVk∑HkT
合理地选择自适应因子不但能够自适应地平衡动力学模型预测信息与量测信息的权比,而且能够控制动力学模型扰动异常对滤波解的影响。基于预测残差误差判别统计量的抗差自适应因子函数为:
等价权矩阵为:
上式中,
P
‾
k
\overline{P}_k
Pk为观测向量的等价权矩阵,
P
k
=
∑
k
−
1
{P}_k=\sum_{k}^{-1}
Pk=∑k−1,
P
X
‾
k
=
∑
X
‾
k
−
1
P_{\overline{X}_k}=\sum_{\overline{X}_k}^{-1}
PXk=∑Xk−1
α
k
\alpha_k
αk ≤1 ,其它符号意义同前。

K
k
=
(
H
k
T
P
‾
k
H
k
+
α
k
P
X
‾
k
)
−
1
H
k
T
P
‾
k
K_k=(H^T_k\overline{P}_kH_k+\alpha_kP_{\overline{X}_k})^{-1}H_k^T\overline{P}_k
Kk=(HkTPkHk+αkPXk)−1HkTPk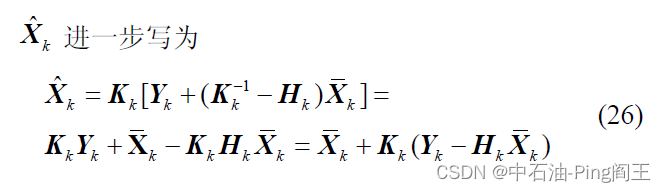
式中:
K
k
K_k
Kk 为增益矩阵,根据矩阵恒等式,可表示为:
K
k
=
α
k
P
X
‾
k
H
k
T
(
H
k
α
k
P
X
‾
k
H
k
T
+
P
‾
k
)
−
1
K_k=\alpha_kP_{\overline{X}_k}H_k^T(H_k\alpha_kP_{\overline{X}_k}H_k^T+\overline{P}_k)^{-1}
Kk=αkPXkHkT(HkαkPXkHkT+Pk)−1
对量测信息采用抗差估计,自适应的确定观测噪声协方差矩阵,并利用自适应因子调节状态噪声的协方差矩阵,因此,可以有效的控制量测异常和动态模型噪声异常对空间状态参数估值的影响。
四、实验结果
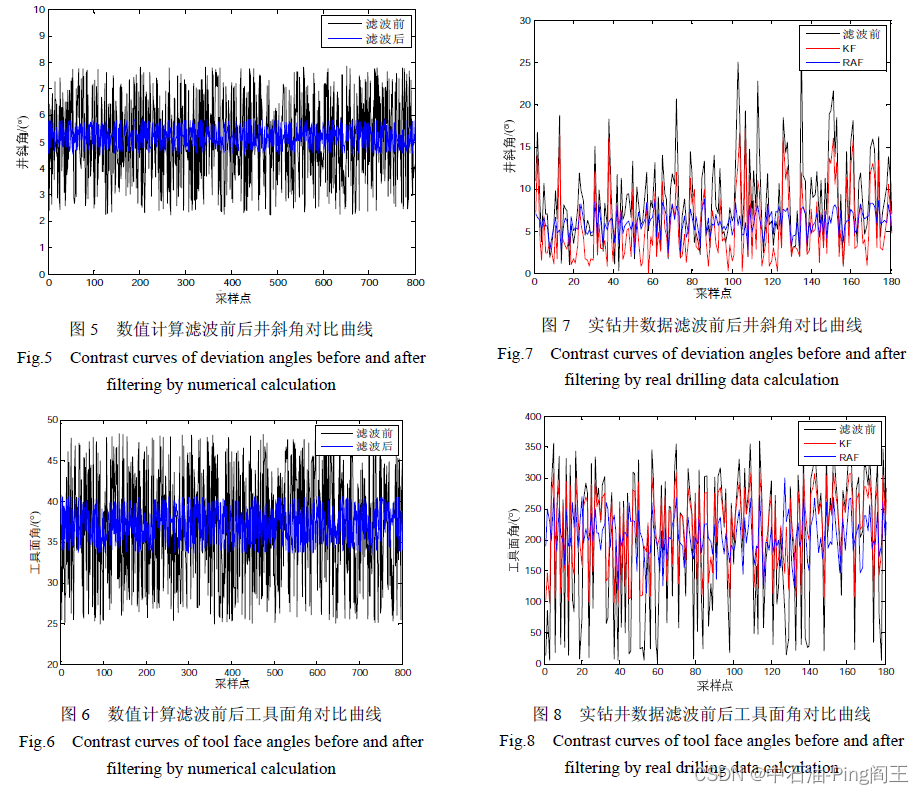
实验室地理条件为北纬34.24°,东经108.99°,地球自转角速度为15 (°)/h,磁倾角为55.4°,磁场强度为52.5 T,地球重力加速度为9.8 m/s2。在实验室条件下,根据测斜校验装置测量得到一组理想的实验数据。
五、往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法