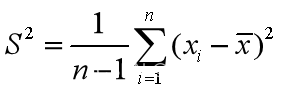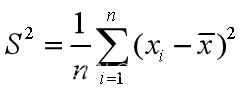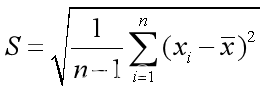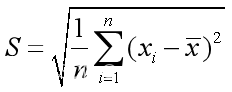目录
1、均值(数学期望)
2、中位数
3、几何平均数
4、调和平均数
5、数据排序
6、众数
7、极差(最大值和最小值之差)
8、方差与均方差(标准差)
9、变异系数
10、常见分布的期望与方差的计算
11、协方差和相关系数
12、偏度和峰度
12.1 偏度
12.2 峰度
1、均值(数学期望)
mean(X):当样本X是向量时,返回X的个元素的算数平均值;当X是矩阵时,返回X的各列元素的平均值。
mean(X ,dim):当dim=1时,返回矩阵X各列的均值 ;当dim=2时,返回矩阵各行的均值。
>> clear
>> R=rand(3,4)
R =
0.9572 0.1419 0.7922 0.0357
0.4854 0.4218 0.9595 0.8491
0.8003 0.9157 0.6557 0.9340
>> a=mean(R,1)
a =
0.7476 0.4931 0.8025 0.6063
>> b=mean(R,2)
b =
0.4817
0.6789
0.8264
2、中位数
median(X) median(X,dim)
Dim=1时,返回矩阵X各列大小排列后位于中间那个数的值(中位数);dim=2时返回各行的中位数。
>> clear
>> R=unidrnd(10,5,5)
R =
4 4 10 4 7
10 3 10 9 8
4 5 6 1 7
2 1 1 1 5
8 2 3 2 6
>> a=median(R,1)
a =
4 3 6 2 7
>> b=median(R,2)
b =
4
9
5
1
3
3、几何平均数

geomean(X) geomean(X,dim)
>> clear
>> R=unidrnd(5,3,4)
R =
2 4 4 5
4 1 4 4
1 2 1 3
>> a=geomean(R,1)
a =
2.0000 2.0000 2.5198 3.9149
>> b=geomean(R,2)
b =
3.5566
2.8284
1.5651
4、调和平均数

harmmean(X) harmmean(X,dim)
>> clear
>> R=rand(3,4)
R =
0.4359 0.5085 0.7948 0.8116
0.4468 0.5108 0.6443 0.5328
0.3063 0.8176 0.3786 0.3507
>> a=harmmean(R,1)
a =
0.3848 0.5828 0.5503 0.5033
>> b=harmmean(R,2)
b =
0.5925
0.5246
0.4008
5、数据排序
sort(X) sort(X,dim)
当X是向量时,返回X从小大到的排序;当dim=1时,对各列独立排序;当dim=2时,对各行独立排序。
>> clear
>> R=unidrnd(10,4)
R =
10 6 3 2
9 3 9 3
6 4 2 5
7 5 3 4
>> sort(R,1)
ans =
6 3 2 2
7 4 3 3
9 5 3 4
10 6 9 5
>> sort(R,2)
ans =
2 3 6 10
3 3 9 9
2 4 5 6
3 4 5 7
sortrows(X):X为向量时,返回X的从小到大的排序;当X时矩阵时,返回按照X第一列元素从小到大的行相关排序。例如
>> clear
>> R=unidrnd(10,4,4)
R =
7 3 7 5
2 1 4 4
8 1 10 8
1 9 1 8
>> a=sortrows(R)
a =
1 9 1 8
2 1 4 4
7 3 7 5
8 1 10 8
sortrows(X,col):当col=k时,表示排序按照第k列元素从小到大的行关联排序,例如
>> clear
>> R=unidrnd(10,4,4)
R =
2 8 7 10
5 8 2 4
5 3 2 6
7 7 5 3
>> b=sortrows(R,3)
b =
5 8 2 4
5 3 2 6
7 7 5 3
2 8 7 10
6、众数
mode(X,dim ) 样本观测值中出现频率最高的数。
>> clear
>> R=unidrnd(8,4,5)
R =
8 4 2 1 1
3 2 8 2 1
1 4 8 3 2
7 1 5 7 6
>> a=mode(R,1)
a =
1 4 8 1 1
>> b=mode(R,2)
b =
1
2
1
7
7、极差(最大值和最小值之差)
range(X,dim);若X是向量,返回X的极差;dim=1时,返回X各列的极差;dim=2时,返回X的各列的极差。
>> clear
>> R=rand(4)
R =
0.7513 0.8909 0.1493 0.8143
0.2551 0.9593 0.2575 0.2435
0.5060 0.5472 0.8407 0.9293
0.6991 0.1386 0.2543 0.3500
>> a=range(R,1)
a =
0.4962 0.8207 0.6914 0.6857
>> b=range(R,2)
b =
0.7416
0.7158
0.4233
0.5605
8、方差与均方差(标准差)
var(X):当X为向量时,返回X的样本方差
当X为矩阵时,返回X各列的方差。
var(X,1):返回X的简单方差
>> clear
>> R=rand(3)
R =
0.1966 0.4733 0.5853
0.2511 0.3517 0.5497
0.6160 0.8308 0.9172
>> S1=var(R)
S1 =
0.0520 0.0620 0.0411
>> S2=var(R,1)
S2 =
0.0347 0.0414 0.0274
std(X):返回X各列的标准差
std(X,1):返回X各列的简单标准差
std(X,flag,dim):flag=0,计算标准差, flag=1,计算简单标准差; dim=1,按列计算; dim=2,按行计算。
9、变异系数
变异系数是衡量数据观测值中各个变量变异程度的一个统计量,定义为
>> clear
R1=normrnd(2,4,10,1);
R2=normrnd(4,4,10,1);
[R1,R2]
ans =
-0.8480 -2.0246
-2.6968 2.2215
1.2310 3.3762
0.9037 5.1043
8.1203 2.9553
1.0039 5.7737
-2.2569 5.5676
8.4138 -1.0027
6.9387 0.2082
1.0815 1.0356
>> [std(R1)/mean(R1),std(R2)/mean(R2)]
ans =
1.8930 1.1821
可见,样本R1的变异程度高于R2的变异程度。
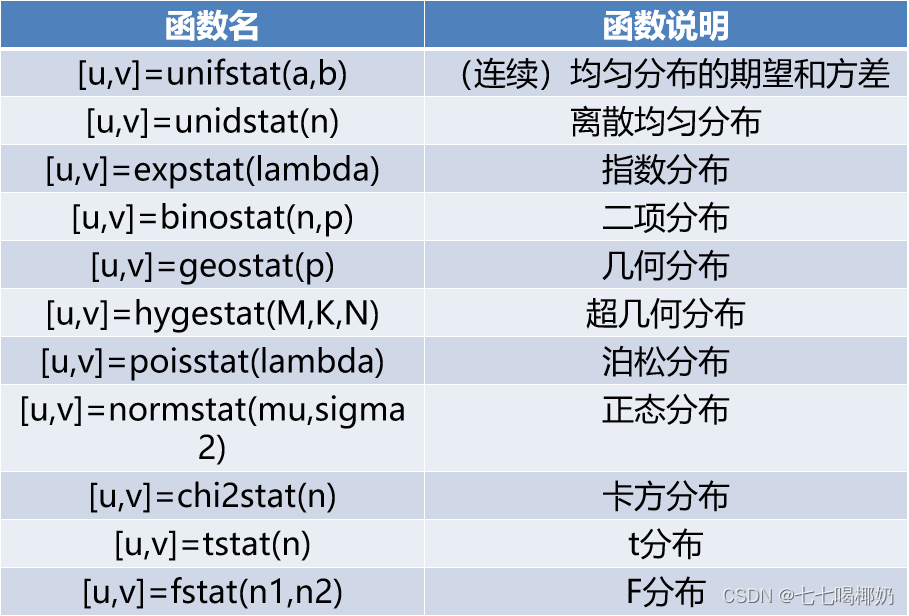
10、常见分布的期望与方差的计算
11、协方差和相关系数
cov(X,dim) 当X为向量时,返回X的方差;当X为矩阵时,返回X各列之间的协方差。
>> clear
>> X=rand(4)
X =
0.7482 0.9133 0.9961 0.9619
0.4505 0.1524 0.0782 0.0046
0.0838 0.8258 0.4427 0.7749
0.2290 0.5383 0.1067 0.8173
>> a=cov(X)
a =
0.0837 0.0088 0.0762 0.0023
0.0088 0.1177 0.1195 0.1349
0.0762 0.1195 0.1822 0.1167
0.0023 0.1349 0.1167 0.1856
R=corrcoef(X) 返回矩阵X各列之间的相关系数。
[r,p,pl,pu]=corrcoef(X)
- r为X各列相关系数;
- p为矩阵X不相关假设检验的p值;
- pl,pu是r的95%置信区间的下限和上限。
>> clear
>> X=[1 2 3 4;2 3 4 5;3 4 5 6;0.2 0.4 0.8 0.9];
>> [r,p,pl,pu]=corrcoef(X)
>> X
X =
1.0000 2.0000 3.0000 4.0000
2.0000 3.0000 4.0000 5.0000
3.0000 4.0000 5.0000 6.0000
0.2000 0.4000 0.8000 0.9000
r =
1.0000 0.9846 0.9651 0.9367
0.9846 1.0000 0.9960 0.9835
0.9651 0.9960 1.0000 0.9957
0.9367 0.9835 0.9957 1.0000
p =
1.0000 0.0154 0.0349 0.0633
0.0154 1.0000 0.0040 0.0165
0.0349 0.0040 1.0000 0.0043
0.0633 0.0165 0.0043 1.0000
pl =
1.0000 0.4366 0.0556 -0.2446
0.4366 1.0000 0.8185 0.4098
0.0556 0.8185 1.0000 0.8039
-0.2446 0.4098 0.8039 1.0000
pu =
1.0000 0.9997 0.9993 0.9987
0.9997 1.0000 0.9999 0.9997
0.9993 0.9999 1.0000 0.9999
0.9987 0.9997 0.9999 1.0000
以5%为置信度,可以看出,第1列和第4列不相关(p>5%),且相关系数的95%置信区间显著包含0,即相关性较弱。
12、偏度和峰度
12.1 偏度

y=skewness(X) 偏度是描述样本数据围绕其均值对称情况的描述,如果y<0,则数据分布偏向均值左边(左偏);反之为右偏。
>> clear
>> x=0:0.1:15;
>> X=chi2pdf(x,5);
>> plot(x,X,'*');
>> y=skewness(X)
y =
0.4090

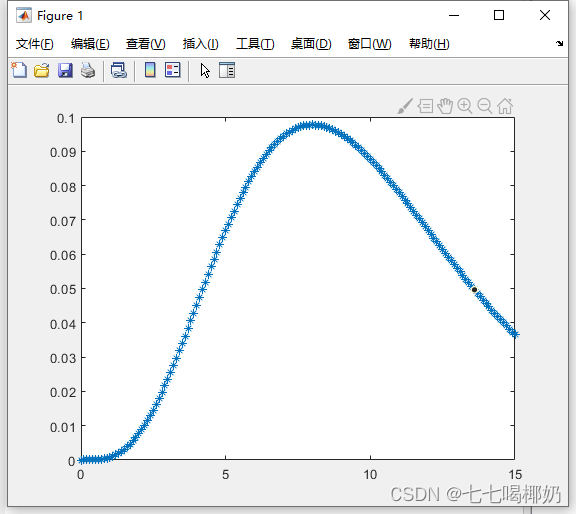
>> x=0:0.1:15;
>> X1=chi2pdf(x,10);
>> plot(x,X1,'*'),y=skewness(X1)
y =
-0.4681
12.2 峰度

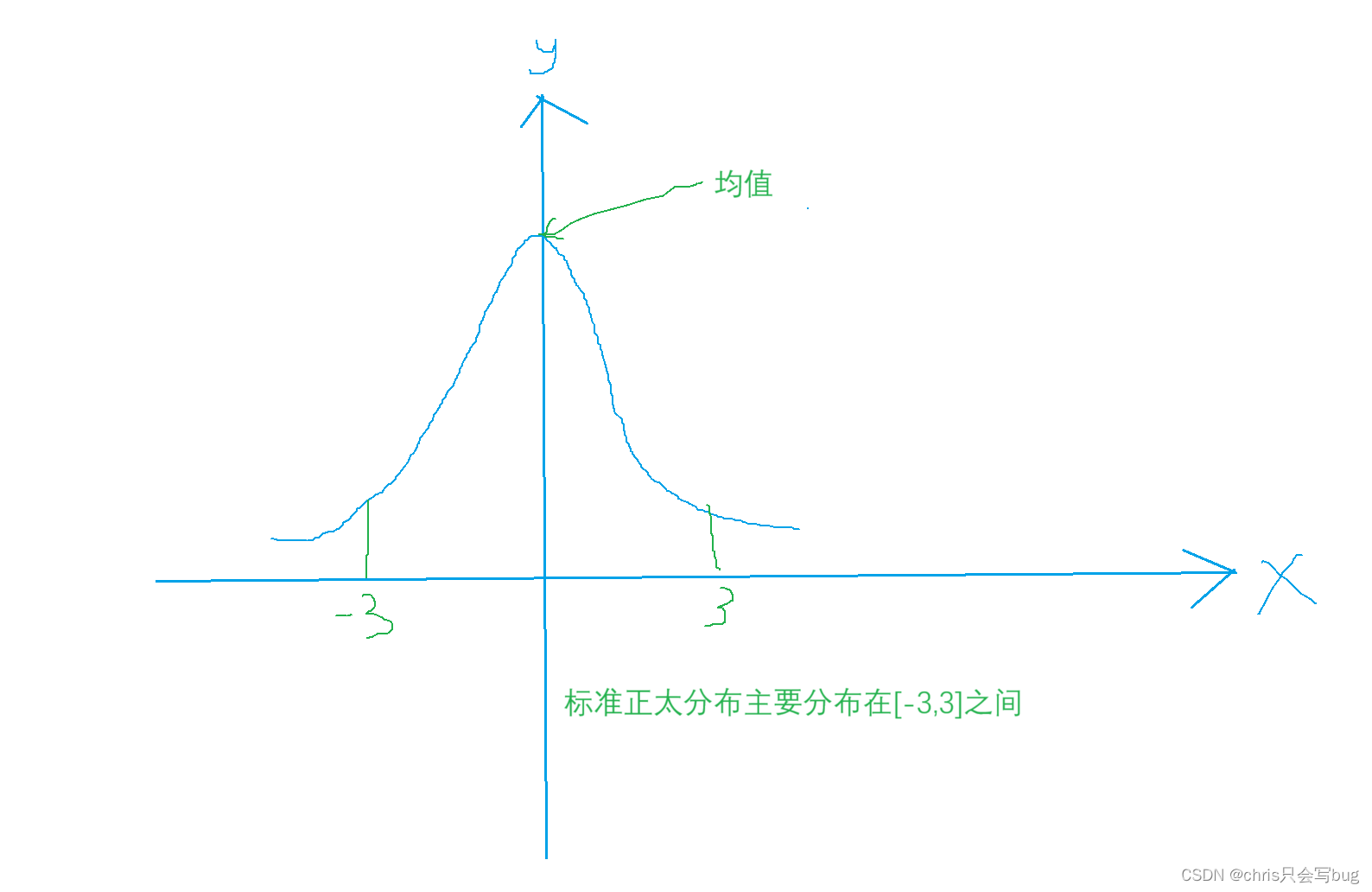
y=kurtosis(X) 若y=3称样本数据呈正态峰度;若r>3,样本曲线比标准正态分布平坦;r<3,样本曲线比标准正态分布陡峭。
>> clear
>> y=[];
>> r=3:0.05:6;
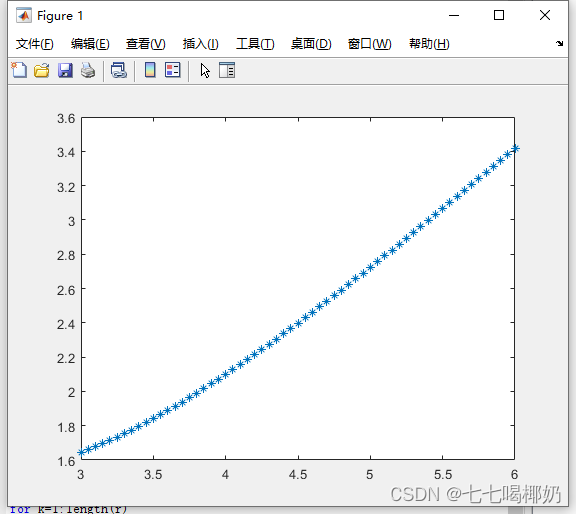
>> for k=1:length(r)
x=-r(k):0.1:r(k);
X=normpdf(x,0,1);
y1=kurtosis(X);
y=[y,y1];
end
>> plot(r,y,'*')