二叉搜索树与常见的查找算法有什么区别?
首先,如果有同学不知道有哪些查找算法可以查看:常见查找算法_加瓦不加班的博客-CSDN博客
如果还有一些不了解的,请查看加瓦不加班_数据结构,链表,递归-CSDN博客
接下来,我们来讲解本章重点:
不管是之前学过的数组、链表、队列、还是栈,这些线性结构中,如果想在其中查找一个元素,效率是比较慢的,只有O(N),因此如果你的需求是实现数据的快速查找,那么就需要新的数据结构支持。
还记得最先介绍的那个二分查找算法吗?它的查找效率能够达到 O(logN),是不是还不错?不过呢,它需要对数组事先排好序,而排序的成本是比较高的。那么有没有一个折中的办法呢?有,那就是接下来要给大家介绍的二叉搜索树,它插入元素后,自然就是排好序的,接下来的查询也自然而然可以应用二分查找算法进行高效搜索。
二叉搜索树
历史

特性
二叉搜索树(也称二叉排序树)是符合下面特征的二叉树:
树节点增加 key 属性,用来比较谁大谁小,key 不可以重复
对于任意一个树节点,它的 key 比左子树的 key 都大,同时也比右子树的 key 都小,例如下图所示

轻易看出要查找 7 (从根开始)自然就可应用二分查找算法,只需三次比较
与 4 比,较之大,向右找
与 6 比,较之大,继续向右找
与 7 比,找到
查找的时间复杂度与树高相关,插入、删除也是如此。
如果这棵树长得还不赖(左右平衡)上图,那么时间复杂度均是 O(\log{N})
当然,这棵树如果长得丑(左右高度相差过大)下图,那么这时是最糟的情况,时间复杂度是 O(N)
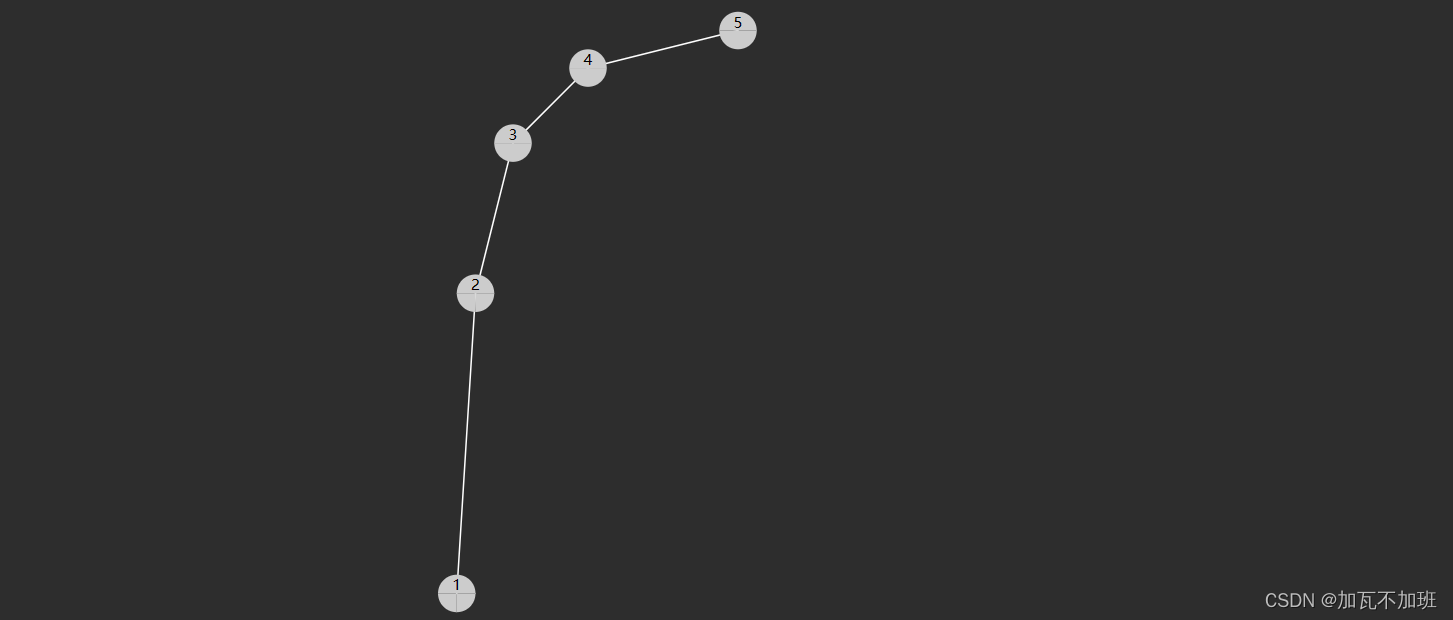
注:
二叉搜索树 - 英文 binary search tree,简称 BST
二叉排序树 - 英文 binary ordered tree 或 binary sorted tree
定义节点
static class BSTNode {
int key; // 若希望任意类型作为 key, 则后续可以将其设计为 Comparable 接口
Object value;
BSTNode left;
BSTNode right;
public BSTNode(int key) {
this.key = key;
this.value = key;
}
public BSTNode(int key, Object value) {
this.key = key;
this.value = value;
}
public BSTNode(int key, Object value, BSTNode left, BSTNode right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}