微积分 - 隐函数求导的应用

news2024/11/29 0:54:24

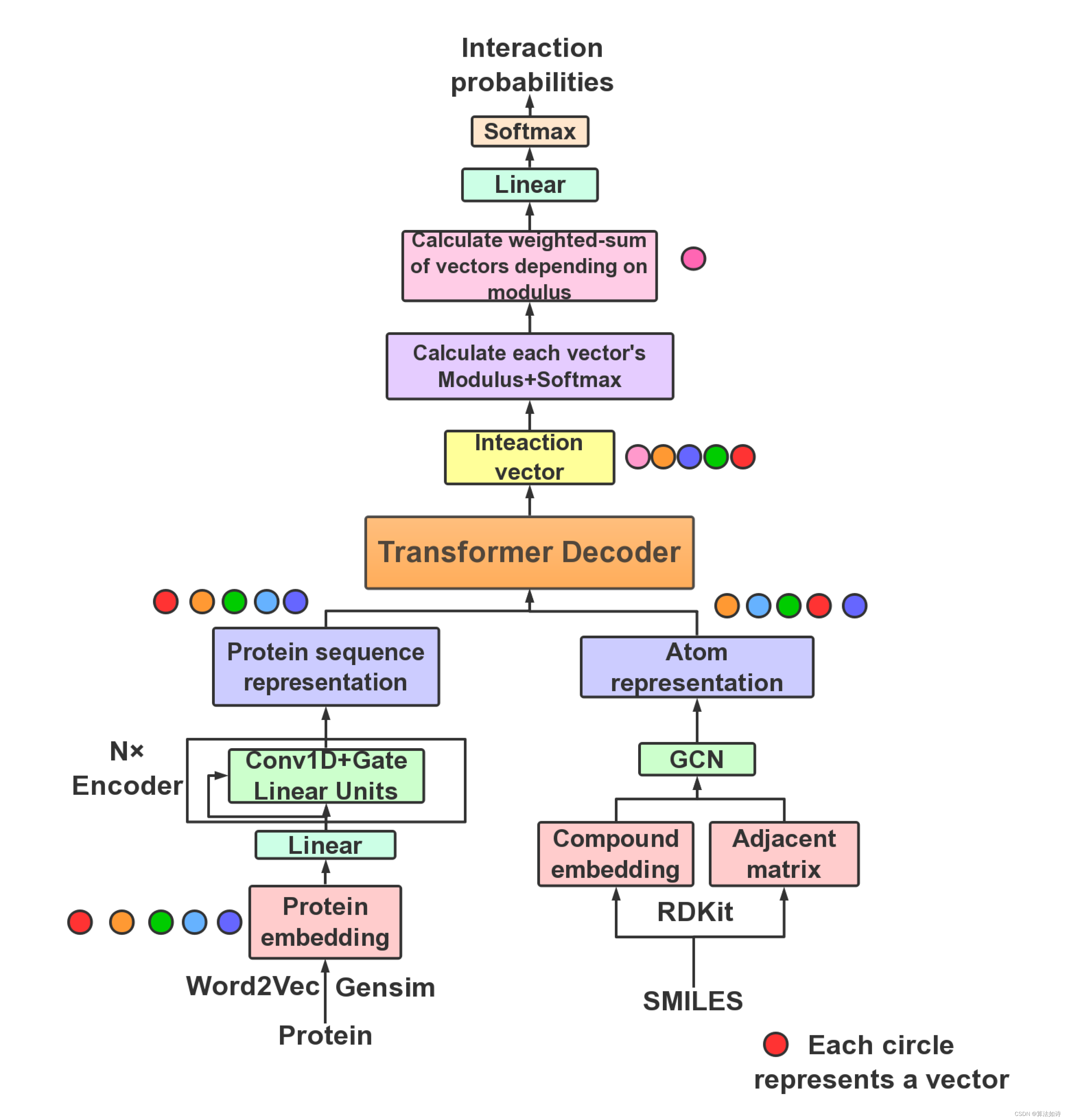
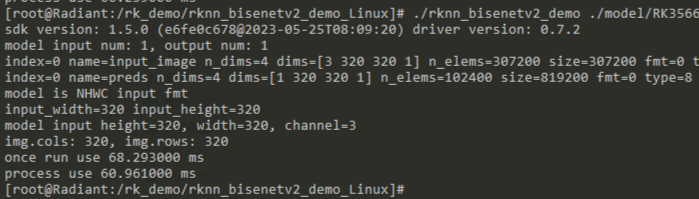
前置理论

已知y与x有关系，那么如何求解 $\frac{d}{dx}(y^{2})$

令u = $y^{2}$ ,则有du/dy = 2y,利用链式求导法则:

$\frac{d}{dx}(y^{2}) = \frac{du}{dx} = \frac{du}{dy}*\frac{dy}{dx} = 2y\frac{dy}{dx}$

一个简单的例子

用一个打气筒给一个完美球体充气，空气以常数速率12 $\pi$ 立方米每秒进入气球，当气球的半径到达2米时，气球半径的变换率是多少？此外，当气球的体积达到36 $\pi$ 立方米时，气球半径的变换率又是多少？

首先我们知道球体的体积为： $V=\frac{4}{3}\pi r^{3}$

我们对方程两边关于t做隐函数求导： $\frac{d}{dt}V = \frac{d}{dt}(\frac{4}{3}\pi r^{3})$

令 $s = r^{3}$ 则有 $ds/dr = 3r^{2}$ ,根据链式求导法则： $\frac{ds}{dt} = \frac{ds}{dr}\frac{dr}{dt} = 3r^{2}\frac{dr}{dt}$

代入方程： $\frac{dV}{dt} = \frac{4}{3}\pi (3r^{2}\frac{dr}{dt}) = 4\pi r^{2}\frac{dr}{dt}$

同时我们知道体积的变换速率为12 $\pi$ ，所以有 $12\pi = 4\pi r^{2}\frac{dr}{dt}$

化简得到 $\frac{dr}{dt} = \frac{3}{r^{2}}$

最终我们就到的了：

当气球半径为2米时的气球半径变换率是 $\frac{dr}{dt} = \frac{3}{2^2} = \frac{3}{4}$
当气球体积为36 $\pi$ 立方米时气球的半径为3米，变换率是 $\frac{dr}{dt} = \frac{3}{3^2} = \frac{1}{3}$

一个稍难的例子

假设有两辆汽车A和B，汽车A向北以55公里/小时的速度远离你家，而汽车B向西以45公里/小时的速度靠近你家，当A到达你家北面21公里，B到达你家东面28公里时，两辆汽车间的距离变化率是多少

根据勾股定理我们知道： $a^2 + b^2 = c^2$

对其关于t做隐函数求导有： $2a\frac{da}{dt} + 2b\frac{db}{dt} = 2c\frac{dc}{dt}$

根据题目我们知道A车的速度为55，B车的速度为45，所以 $\frac{da}{dt}$ 为55，但是由于B车是在靠近我们所以 $\frac{db}{dt}$ 为-45，于是有： $a*55 - b*45 = c\frac{dc}{dt}$

最后我们将a = 21,b = 28根据勾股定理c = 35代入后可得： $35\frac{dc}{dt} = 55*21 - 45*28$

得到的结果是-3，于是我们知道在当前时刻，两辆汽车的距离是以3公里/小时靠近。

一个更难的例子

设想有一个巨大的圆锥水箱，锥尖在下方。圆锥的高是圆锥半径的2倍即H=2R，如果水是以8 $\pi$ 立方米/秒的速率注入水箱中，求当水箱中水的体积为18 $\pi$ 立方米时，水位的变换速率是多少？此外，假设水箱底部有一个小洞，致使水箱中的水以每一立方米的水以一立方米的速度向外流水（这里要注意漏水的速度可不是1立方米/秒），这种情况下，水位的变换速率是多少？

首先我们知道圆锥的体积公式为： $V = \frac{1}{3}\pi r^2h$

根据三角形相似性原则，因为▲OCD与▲OAB相似可知： h = 2r

于是有： $V = \frac{1}{3}\pi r^2h = \frac{1}{3}\pi (\frac{h}{2})^2h = \frac{\pi h^3}{12}$

对上式关于t求导： $\frac{dV}{dt} = \frac{\pi }{12} \times 3h^2\frac{dh}{dt} = \frac{\pi h^2}{4} \frac{dh}{dt}$

同时我们知道注水速度为8 $\pi$ 即 $\frac{dV}{dt} = 8\pi$ ,当体积为18 $\pi$ 时h为6于是有： $8\pi = \frac{\pi }{4} \times 6^2 \frac{dh}{dt}$ 可得dh/dt=8/9,也就是说当体积为18 $\pi$ 时水位正在以8/9米/秒的速率上升。

现在我们来考虑下当水箱在注水的同时漏水会怎么样，由于当箱中有v立方米，则漏水的速率为v立方米/秒所以有： $\frac{dV}{dt} = 8\pi - V$

当体积为18 $\pi$ 时： $\frac{dV}{dt} = 8\pi - 18\pi = -10\pi$ 代入上述方程后可以得到dh/dt=-10/9,也就是说当体积为18 $\pi$ 时水位正在以10/9米/秒的速率下降。

一个非常难的例子

设想有一架飞机在2000公里的高空以500公里每秒的速度远离你，同时不久之前有一个跳伞员在距你1000公里远上从直升机上跳下，垂直以10公里每秒的速度落地。当两者在同一高度，飞机在你东边 8000公里时，角 $\theta$ 的变换率是多少？

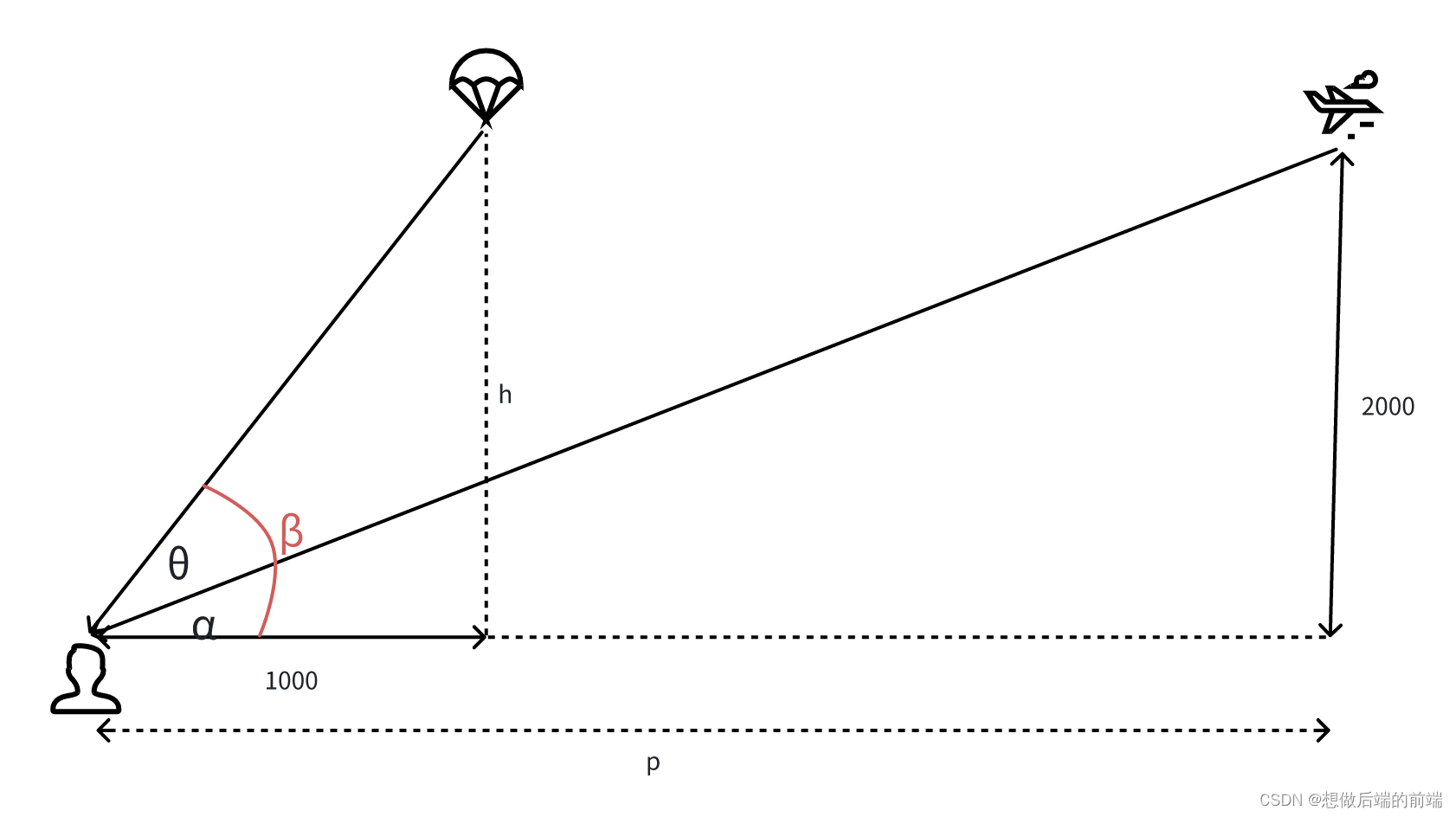
已知1000和2000这两个是始终不变的，但是h和p是会一直变换，其中h会越来越小，而p则会越来越大。

从图中我们可以得到两个关系式： $tan(\alpha ) = \frac{2000}{p}$ 与 $tan(\beta ) = \frac{h}{1000}$

接着我们对上面两个公式关于t做隐函数求导：

令 $\upsilon = tan(\alpha )$ 则有 $\frac{d\upsilon }{dt} = \frac{d\upsilon }{d\alpha } \frac{d\alpha }{dt} = sec^2(\alpha )\frac{d\alpha }{dt}$
令 $\nu = \frac{2000}{p}$ 则有 $\frac{d\nu }{dt} = \frac{d\nu }{dp} \frac{dp}{dt } = -\frac{2000}{p^2} \frac{dp}{dt }$
令 $\upsilon = tan(\beta )$ 则有 $\frac{d\upsilon }{dt} = \frac{d\upsilon }{d\beta } \frac{d\beta }{dt} = sec^2(\beta )\frac{d\beta }{dt}$
令 $\nu = \frac{h}{1000}$ 则有 $\frac{d\nu }{dt} = \frac{d\nu }{dh} \frac{dh}{dt } = \frac{1}{1000} \frac{dh}{dt }$

于是有：

$sec^2(\alpha )\frac{d\alpha }{dt} = -\frac{2000}{p^2} \frac{dp}{dt }$ 代入值有 $sec^2(\alpha )\frac{d\alpha }{dt} = -\frac{2000}{8000^2} \times 500 = -\frac{1}{64}$
$sec^2(\beta )\frac{d\beta }{dt} = \frac{1}{1000} \frac{dh}{dt }$ 代入值有 $sec^2(\beta )\frac{d\beta }{dt} = \frac{1}{1000} \times (-10) = -\frac{1}{100}$