课题学习(四)----四元数解法

news2024/11/24 15:36:56

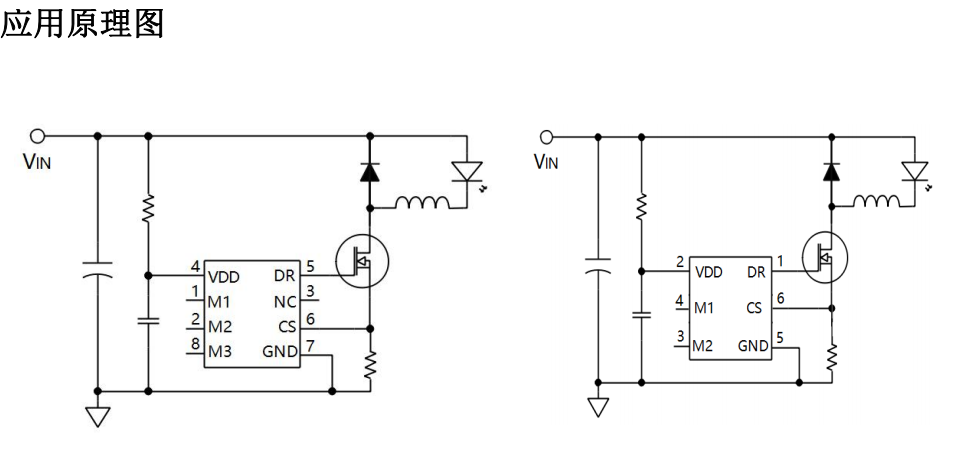
一、四元数解法

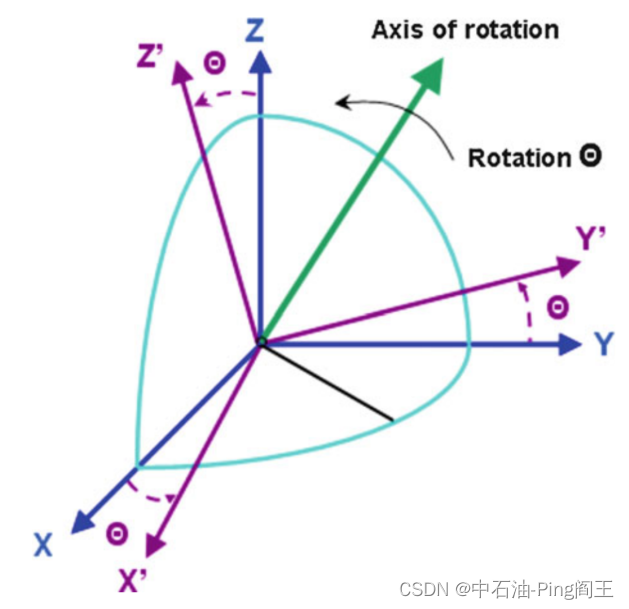
为了求解惯性导航的力学方程，姿态矩阵 $R^b_{b}$ 可以有姿态微分方程得到。其中，四元数是常用的方法，如下图所示，假设刚体在原点旋转，根据欧拉定理，运动坐标系(b系列)相对于导航坐标系(n系列)的方向，相当于b系绕等效轴旋转一个角度Θ。
在这里插入图片描述
用四元数 $Q=\begin{bmatrix}q1 & q2 &q3&q4 \end{bmatrix}^T$ 来描述b系统相对于n系统的旋转。定义如下：
$\begin{bmatrix} q1 \\ q2 \\q3\\q4\end{bmatrix} = \begin{bmatrix} (Θ_{x}/Θ)sin(Θ/2) \\ (Θ_{y}/Θ)sin(Θ/2) \\(Θ_{z}/Θ)sin(Θ/2)\\cos(Θ/2)\end{bmatrix}$
其中， $\sqrt{Θ^2_{x}+Θ^2_{y}+Θ^2_{z}}$ , $Θ_{x}/Θ,Θ_{y}/Θ,Θ_{z}/Θ$ 是n坐标系中的方向余弦。
从四元数的定义来看， $q^2_{1}+q^2_{2}+q^2_{3}+q^2_{4}=1$ ，四元数的分量不是相互独立的，只需要三个独立的四元数分量来描述坐标轴的旋转。然而，通常存在计算误差，定义为 $1-q^2_{1}+q^2_{2}+q^2_{3}+q^2_{4}$ 。为了纠正这一错误，每次计算后都需要将向量形式的四元数Q更新为以下公式:
在这里插入图片描述
用一阶微分方程描述四元数的时域变化: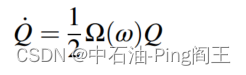

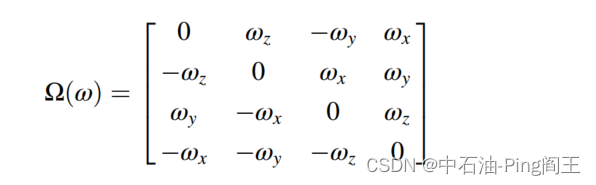
其中, $w_{x},w_{y},w_{z}$ 是载体的角速度。
求解一阶微分方程，根据tk时刻的Qk，求出tk + 1时刻的Qk + 1，如下所示: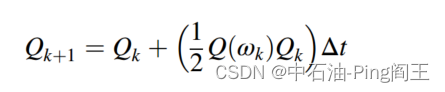
当时刻tk，四元数确定时， $R^n_{b}$ 可直接由下式确定:
$R^n_{b} = \begin{bmatrix} R_{11} &R_{12}&R_{13}\\ R_{21} &R_{22}&R_{23}\\ R_{31} &R_{32}&R_{33} \end{bmatrix}$
$=\begin{bmatrix} q^2_{1}-q^2_{2}-q^2_{3}+q^2_{4} &2(q_{1}q_{2}-q_{3}q_{4})&2(q_{1}q_{2}+q_{3}q_{4})\\ 2(q_{1}q_{2}+q_{3}q_{4}) &-q^2_{1}+q^2_{2}-q^2_{3}+q^2_{4}&2(q_{2}q_{3}-q_{1}q_{4})\\ 2(q_{1}q_{3}-q_{2}q_{4})&2(q_{2}q_{3}+q_{1}q_{4})&-q^2_{1}-q^2_{2}+q^2_{3}+q^2_{4} \end{bmatrix}$
得到四元数的更新方程为:
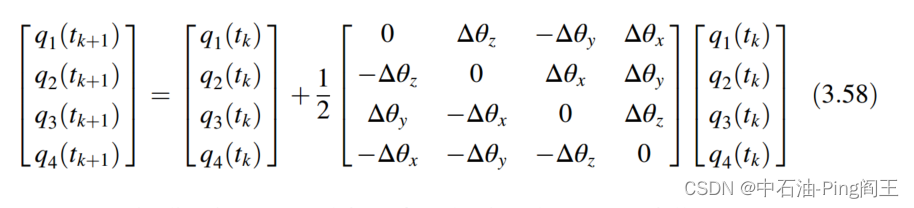
在这里插入图片描述
得到倾角θ，工具面φ和方位ψ如下
$θ=arctan(\frac{R_{32}}{\sqrt{R^2_{12}+R^2_{22}}})$
$\phi=arctan(\frac{-R_{31}}{R_{33}})$
$\psi=arctan(\frac{-R_{12}}{R_{22}})$
进而可得到井斜角 $90-\theta$ .
在捷联导航系统中，由于GPS对准，在建立误差模型后，采用卡尔曼滤波方法可以获得准确的载体姿态和位置信息。但在随钻测量中，无法使用GPS信号校正，需要重新建立卡尔曼滤波模型。随钻陀螺测量系统的卡尔曼滤波模型，由于采用了惯性陀螺仪和加速度传感器，其误差模型与航空航天领域捷联导航的卡尔曼滤波误差模型一致。从可靠性的角度来看，目前在钻井测量领域，基于磁的测量系统比陀螺仪系统更具应用优势。然而，由于磁干扰等因素，磁基系统不可能完全完善。未来的发展方向必然是复合模式测量系统，即磁传感器与陀螺仪系统相结合的随钻测量系统。