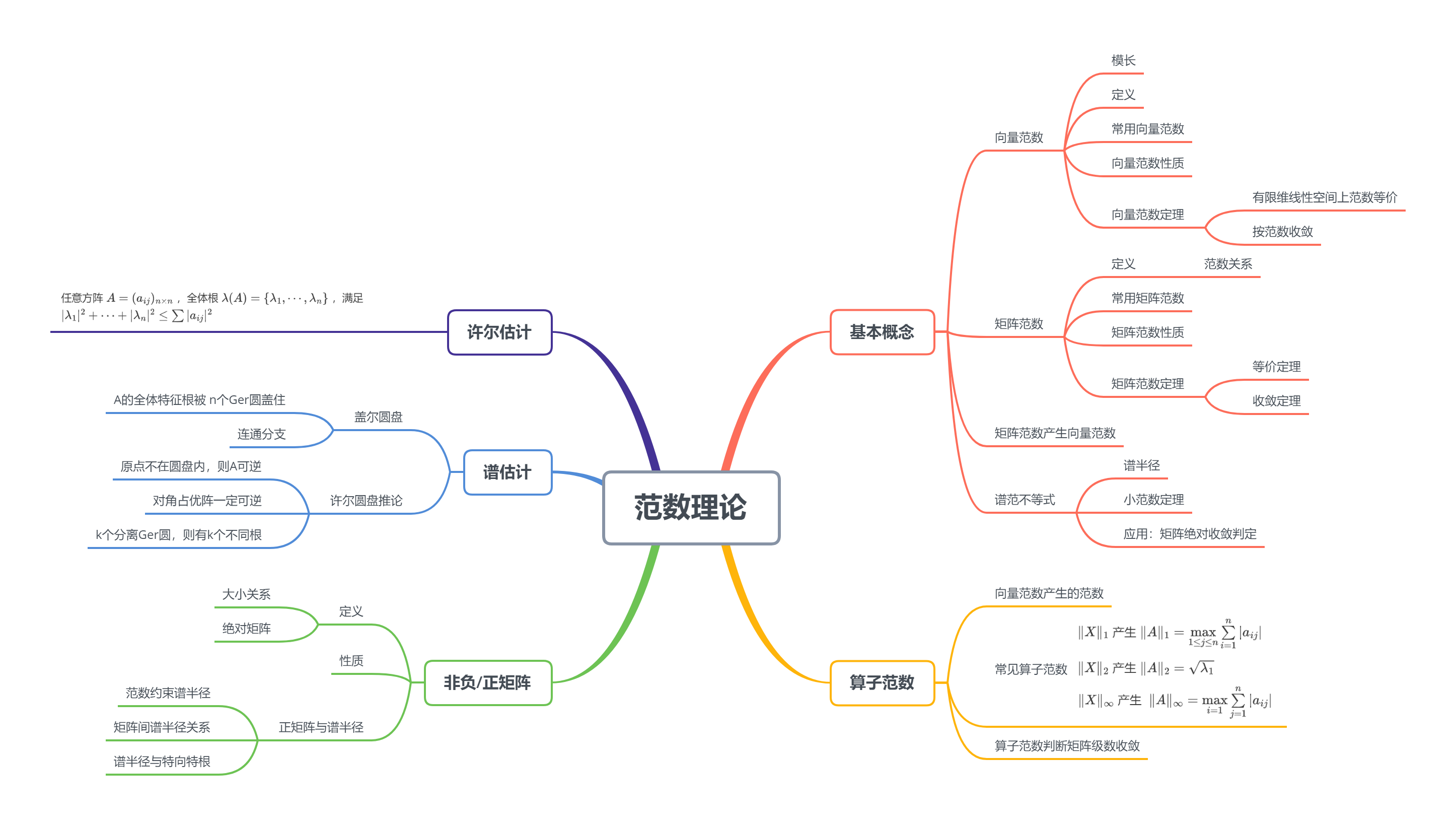
6.2 算子范数

6.2.1 定义

$C^n$ 上任一向量范数 $\Vert X{\Vert }_V$ 都产生一个矩阵范数 ∥ A ∥ = max ⁡ x ≠ 0 { ∥ A X ∥ V ∥ X ∥ V } \Vert A\Vert=\max_{x\neq 0}\limits \{\frac{\Vert AX\Vert_V}{\Vert X\Vert_V}\} ∥A∥=x=0max​{∥X∥V​∥AX∥V​​} ,$X\in C^n$ ，且有相容关系 $\Vert AX{\Vert }_V\le \Vert A\Vert \cdot \Vert X{\Vert }_V$ ，这种范数 $\Vert A\Vert$为算子范数

向量范数生成的矩阵范数

• 若存在常数 M，使 $\forall X\in C^n$ ，有 $\Vert AX{\Vert }_V\le M\Vert X{\Vert }_V$ ，则 $\Vert A\Vert \le M$ ，即 $\Vert X{\Vert }_V$ 的算子范数是使上述不等式成立的最小范数

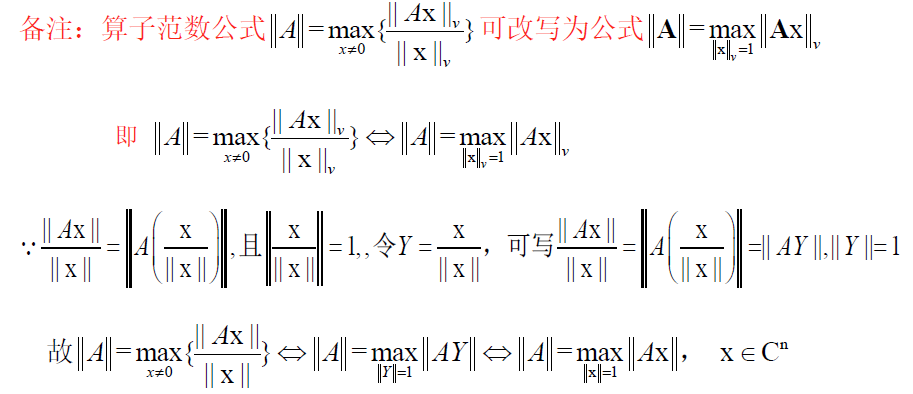
a. 证明算子范数是范数

矩阵范数与向量范数相容性：

∥ A ∥ = max ⁡ X ≠ 0 { ∥ A X ∥ V ∥ X ∥ V } ⇒ ∥ A X ∥ V ∥ X ∥ V ≤ max ⁡ X ≠ 0 { ∥ A X ∥ V ∥ X ∥ V } = ∥ A ∥ ⇒ ∥ A X ∥ V ≤ ∥ A ∥ ⋅ ∥ X ∥ V \begin{aligned} &\Vert A\Vert=\max_{X\neq 0}\{\frac{\Vert AX\Vert_V}{\Vert X\Vert_V}\}\Rightarrow \frac{\Vert AX\Vert_V}{\Vert X\Vert_V}\le \max_{X\neq 0}\{\frac{\Vert AX\Vert_V}{\Vert X\Vert_V}\}=\Vert A\Vert\\ &\Rightarrow \Vert AX\Vert_V\le \Vert A\Vert\cdot \Vert X\Vert_V \end{aligned} ​∥A∥=X=0max​{∥X∥V​∥AX∥V​​}⇒∥X∥V​∥AX∥V​​≤X=0max​{∥X∥V​∥AX∥V​​}=∥A∥⇒∥AX∥V​≤∥A∥⋅∥X∥V​​

• 由于 $\Vert AX{\Vert }_V$ 是X各分量的连续函数，故在有界闭集 $\Vert X{\Vert }_V$ 上可取最大值，因此上述定义是有意义的，即存在 $X_0$ 使 $\underset{\Vert X{\Vert }_V=1}{\max }\Vert AX{\Vert }_V=\Vert A{X}_0{\Vert }_V$ ，在 $X_0$ 处取最大值

6.2.2 常见算子范数

设 $A=\left(a_{ij}\right)\in C^{n.n}，X\in C^n$ ，则向量范数 $\Vert X{\Vert }_1,\Vert X{\Vert }_2,\Vert X{\Vert }_{\infty }$ 产生的算子范数为：

• $\Vert X{\Vert }_1$ 产生 $\Vert A{\Vert }_1=\underset{1\le j\le n}{\max }\sum _{i=1}^n|a_{ij}|$ （列范数），且 $\Vert AX{\Vert }_1\le \Vert A{\Vert }_1\cdot \Vert X{\Vert }_1$
• $\Vert X{\Vert }_2$ 产生 $\Vert A{\Vert }_2=\sqrt{{\lambda }_1},{\lambda }_1为A^{H}A$ 的最大特征值（谱范数），且 $\Vert AX{\Vert }_2\le \Vert A{\Vert }_2\cdot \Vert X{\Vert }_2$
• $\Vert X{\Vert }_{\infty }$ 产生 $\Vert A{\Vert }_{\infty }=\underset{i=1}{\max }\sum _{j=1}^n|a_{ij}|$ （行范数），且 $\Vert AX{\Vert }_{\infty }\le \Vert A{\Vert }_{\infty }\cdot \Vert X{\Vert }_{\infty }$

a. 必要条件

任一矩阵范数 $\Vert I\Vert \ge 1$

• 任一算子范数必有 $\Vert I\Vert =1$

  由公式 ∥ A ∥ = max ⁡ x ≠ 0 { ∥ A X ∥ V ∥ X ∥ V } \Vert A\Vert=\max_{x\neq 0}\limits \{\frac{\Vert AX\Vert_V}{\Vert X\Vert_V}\} ∥A∥=x=0max​{∥X∥V​∥AX∥V​​} ，可知 ∥ I ∥ = max ⁡ X ≠ 0 { ∥ I X ∣ V ∥ X ∥ V } = 1 \Vert I\Vert=\max_{X\neq 0}\limits \{\frac{\Vert IX\vert_V}{\Vert X\Vert_V}\}=1 ∥I∥=X=0max​{∥X∥V​∥IX∣V​​}=1

• 若某个 $\Vert I{\Vert }_{\ast }>1$ ，则 $\Vert \bullet {\Vert }_{\ast }$ 不是算子范数

eg

可见 $\Vert A{\Vert }_F$ 与 $\Vert x{\Vert }_2$ 是相容的，而 $\Vert A{\Vert }_2$ 作为 $\Vert x{\Vert }_2$ 的算子范数是相容的，但与 $\Vert A{\Vert }_F$ 不同

• $\Vert A{\Vert }_2\le \Vert A{\Vert }_F$ ，即 $\Vert X{\Vert }_V$ 的算子范数是使 $\Vert A\Vert \le \frac{\Vert AX{\Vert }_V}{\Vert X{\Vert }_V}$ 成立的最小范数

6.2.3 算子范数判断矩阵级数收敛

a. 矩阵级数收敛定义

$$\begin{array}{rl}& \sum _{k=0}^{\infty }{A}_k=A_0+A_1+\cdots +A_k+\cdots 收敛于A⟺\underset{k\to \infty }{\lim }(A_0+A_1+\cdots +A_k)=A\\ & 其中A_k\in C^{n,n},记为\sum _{k=0}^{\infty }{A}_k=A_0+A_1+\cdots +A_k=A\end{array}$$

绝对收敛本身必收敛 ： 若 $\sum _{k=0}^{\infty }\Vert A_k\Vert =\Vert A_0\Vert +\Vert A_1\Vert +\cdots +\Vert A_k\Vert +\cdots$ 收敛，则 $\sum _{k=0}^{\infty }{A}_k$ 收敛

• 若某个范数 $\Vert A\Vert <1$ ，则 $\sum _{k=0}^{\infty }{A}^k$ 绝对收敛

  证明：
  $$\begin{array}{rl}& \Vert A\Vert <1\Rightarrow \Vert A^k\Vert \le \Vert A{\Vert }^k且\sum _{k=0}^{\infty }\Vert A{\Vert }^k=\frac{\Vert I\Vert }{I-\Vert A\Vert }(绝对收敛)\end{array}$$

• $\rho (A)<1\Rightarrow \sum _{k=0}^{\infty }{A}^k$ 绝对收敛
  $$\rho (A)<1\Rightarrow 某范数\Vert A\Vert <1\Rightarrow \sum _{k=0}^{\infty }{A}^k绝对收敛$$

**若 $\rho (A)<1$ ，则 $\sum _{k=0}^{\infty }{A}^k=(I-A{)}^{-1}$ **

证明：
$$\begin{array}{rl}& (I-A)(I+A+\cdots +A^k+\cdots )=I(I+A+\cdots +A^k+\cdots )-A(I+A+\cdots +A^k+\cdots )\\ & =(I+A+\cdots +A^k+\cdots )-(A+\cdots +A^k+\cdots )=I\\ & \therefore (I-A{)}^{-1}=\sum _{k=0}^{\infty }{A}^k=I+A+\cdots +A^k+\cdots \end{array}$$

• 若 $\Vert A\Vert <1$ ，则 $\sum _{k=0}^{\infty }{A}^k=(I-A{)}^{-1}$

b. 幂级数收敛

设幂级数 $\sum _{k=0}^{\infty }{c}_k{x}^k$ 的收敛半径为 $R$ ，则

• $\rho (A)<R\Rightarrow \sum _{k=0}^{\infty }{c}_k{A}^k$ 绝对收敛
• 某一范数 $\Vert A\Vert <R\Rightarrow \sum _{k=0}^{\infty }{c}_k{A}^k$ 绝对收敛
• 若 $\rho (A)>R$ ，则 $\sum _{k=0}^{\infty }{c}_k{A}^k$ 发散
• $\rho (A)=R$ ，$\sum _{k=0}^{\infty }{c}_k{A}^k$ 都有可能

SP：

• $e^x=\sum _{k=0}^{\infty }\frac{1}{k!}{x}^k$ ，

  $sinx=\sum _{k=0}^{\infty }(-1{)}^k\frac{x^{2k+1}}{(2k+1)!}$

  $cosx=\sum _{k=0}^{\infty }(-1{)}^k\frac{x^{2k}}{(2k)!}$ 的收敛半径都是 $R=+\infty$ ，故任意方阵都满足收敛条件 $\rho (A)<R$

$e^A=\sum _{k=0}^{\infty }\frac{1}{k!}{A}^k$ ，$sinA=\sum _{k=0}^{\infty }(-1{)}^k\frac{A^{2k+1}}{(2k+1)!}$ ，$cosA=\sum _{k=0}^{\infty }(-1{)}^k\frac{A^{2k}}{(2k)!}$ 都绝对收敛

---

• $ln(1+x)=\sum _{k=1}^{\infty }(-1{)}^{k-1}\frac{x^k}{k}$ 的收敛半径为 $r=1$ ，

  $(1-x{)}^{-1}=1+x+\cdots +x_{\cdots }^k$ 的收敛半径 $r=1$

  $(1-x{)}^{-2}=1+x+2x+3x^2+\cdots +k{x}^{k-1}+\cdots$ 的收敛半径 $r=1$

$ln(I+A)=\sum _{k=1}^{\infty }(-1{)}^{k-1}\frac{A^k}{k}$ 的绝对收敛条件为 $\rho (A)<1$ 或 $\Vert A\Vert <1$

$(I-A{)}^{-1}=\sum _{k=0}^{\infty }{A}^k$ 的绝对收敛条件为 $\rho (A)<1$ 或 $\Vert A\Vert <1$

$(I-A{)}^{-2}=\sum _{k=1}^{\infty }k{A}^{k-1}$ 的绝对收敛条件是 $\rho (A)<1$ 或 $\Vert A\Vert <1$