目录
(反)序列化二叉树(str<->tree):前序
前序遍历(迭代)/路径
stack.length
入栈:中右左
出栈:中左右
中序遍历(迭代)
cur||stack.length
后序遍历(迭代)
和前序遍历不同:
入栈:中左右
出栈:中右左
reverse出栈:左右中
层序遍历(BFS):可求树的深/高度
找树左下角的值:最后一行的最左边的值
判断完全二叉树
queue.length
flag = false; //是否遇到空节点
判断平衡二叉树
递归Math.max(getMaxDepth(root.left)+1,getMaxDepth(root.right)+1)
判断对称二叉树
递归deep(left.left, right.right) && deep(left.right, right.left)
翻转/生成镜像二叉树
递归交换左右
两节点的最近公共祖先
递归后序遍历
构造二叉树
从中序与前/后序遍历序列构造二叉树
最大二叉树:二叉树的根是数组中的最大元素(递归定义)
二叉搜索树:左<根<右(按中序遍历有序的树)
删除二叉搜索树中的节点
修剪二叉搜索树
有序数组转换为平衡二叉搜索树
left, right比arr.slice高效
Math.floor(left + (right - left) / 2)
最值、差值->有序数组的差值、最值
二叉搜索树的最小绝对差
二叉搜索树转换为累加树
(反)序列化二叉树(str<->tree):前序
function TreeNode(x) {
this.val = x;
this.left = null;
this.right = null;
}
//反序列化二叉树:tree->str 把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串
function Serialize(pRoot, arr = []) {
if (!pRoot) {
arr.push("#");
return arr;
} else {
arr.push(pRoot.val);//注意是val。而不是root
Serialize(pRoot.left, arr);
Serialize(pRoot.right, arr);
}
return arr;
}
//序列化二叉树:str->tree 根据字符串结果str,重构二叉树
function Deserialize(s) {
//转换为数组
let arr = Array.isArray(s) ? s : s.split("");
//取出val
let a = arr.shift();
//构建二叉树结点
let node = null;
if (typeof a === "number") {
//还有可能等于#
node = new TreeNode(a);
node.left = Deserialize(arr);
node.right = Deserialize(arr);
}
return node;
}
module.exports = {
Serialize: Serialize,
Deserialize: Deserialize,
};
前序遍历(迭代)/路径
stack.length
入栈:中右左
出栈:中左右
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var preorderTraversal = function(root) {
let stack=[]
let res = []
let cur = null;
if(!root) return res;
root&&stack.push(root)
while(stack.length){
cur = stack.pop()
res.push(cur.val)
cur.right&&stack.push(cur.right)
cur.left&&stack.push(cur.left)
}
return res
};
中序遍历(迭代)
cur||stack.length
指针的遍历来帮助访问节点,栈则用来处理节点上的元素
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var inorderTraversal = function(root) {
let stack = []
let res = []
let cur = root
while(cur||stack.length){
if(cur){
stack.push(cur)
cur = cur.left
} else {
cur = stack.pop()
res.push(cur.val)
cur = cur.right
}
}
return res
};
后序遍历(迭代)
和前序遍历不同:
入栈:中左右
出栈:中右左
reverse出栈:左右中
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var postorderTraversal = function(root) {
let stack = []
let res = []
let cur = root
if(!root) return res
stack.push(root)
while(stack.length){
cur = stack.pop()
res.push(cur.val)
cur.left&&stack.push(cur.left)
cur.right&&stack.push(cur.right)
}
return res.reverse()
};
层序遍历(BFS):可求树的深/高度
树的层序遍历,相似 图的广度优先搜索
- 初始设置一个空队,根结点入队
- 队首结点出队,其左右孩子 依次 入队
- 若队空,说明 所有结点 已处理完,结束遍历;否则(2)
/*
* function TreeNode(x) {
* this.val = x;
* this.left = null;
* this.right = null;
* }
*/
/**
*
* @param root TreeNode类
* @return int整型二维数组
*/
function levelOrder(root) {
// write code here
if (root == null) {
return [];
}
const arr = [];
const queue = [];
queue.push(root);
while (queue.length) {
const preSize = queue.length;
const floor = [];//当前层
for (let i = 0; i < preSize; ++i) {
const v = queue.shift();
floor.push(v.val);
v.left&&queue.push(v.left);
v.right&&queue.push(v.right);
}
arr.push(floor);
}
return arr;//[[1],[2,3]]
}
module.exports = {
levelOrder: levelOrder,
};
找树左下角的值:最后一行的最左边的值
判断完全二叉树
queue.length
flag = false; //是否遇到空节点
完全二叉树:叶子节点只能出现在最下层和次下层,且最下层的叶子节点集中在树的左部。
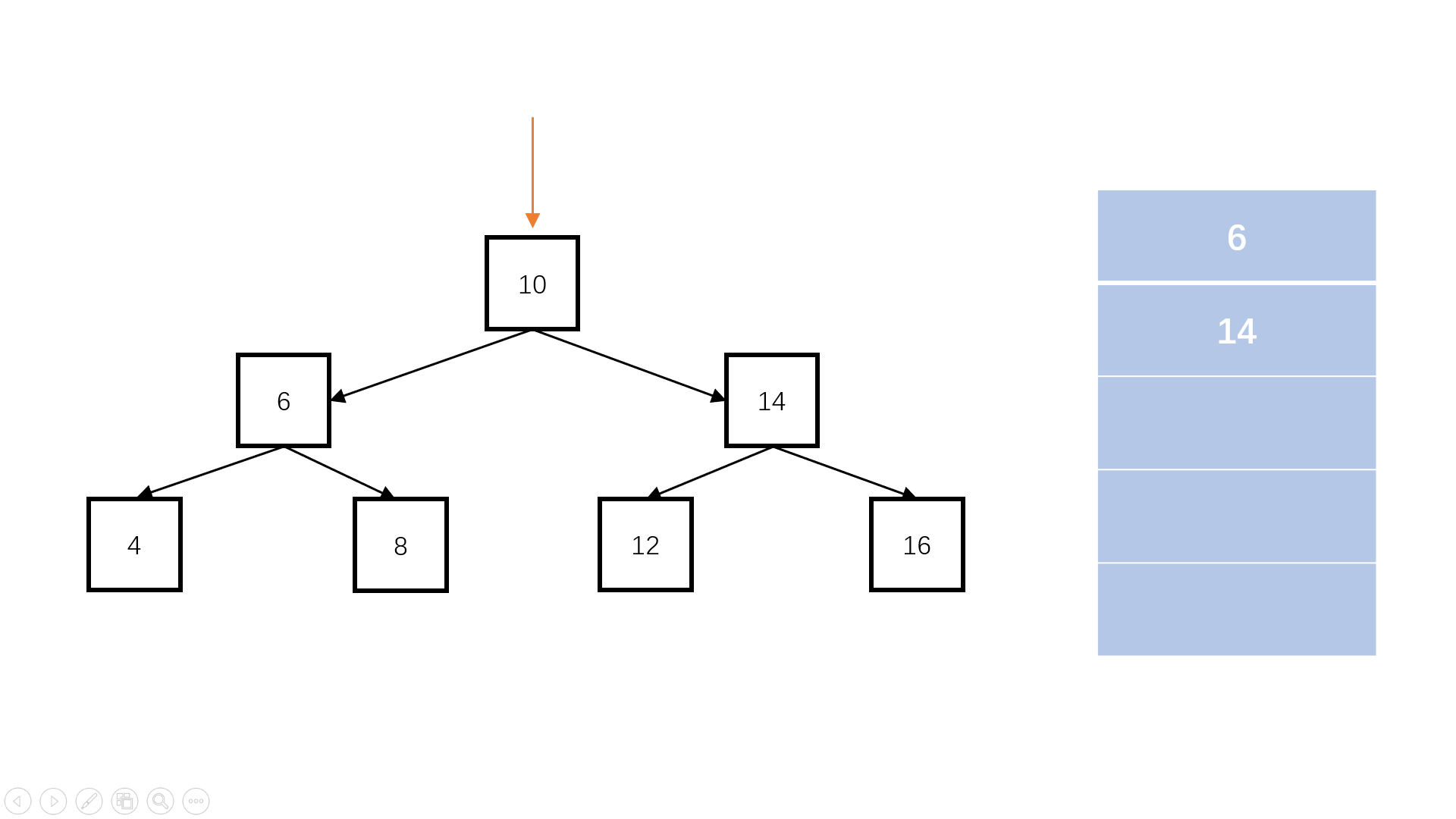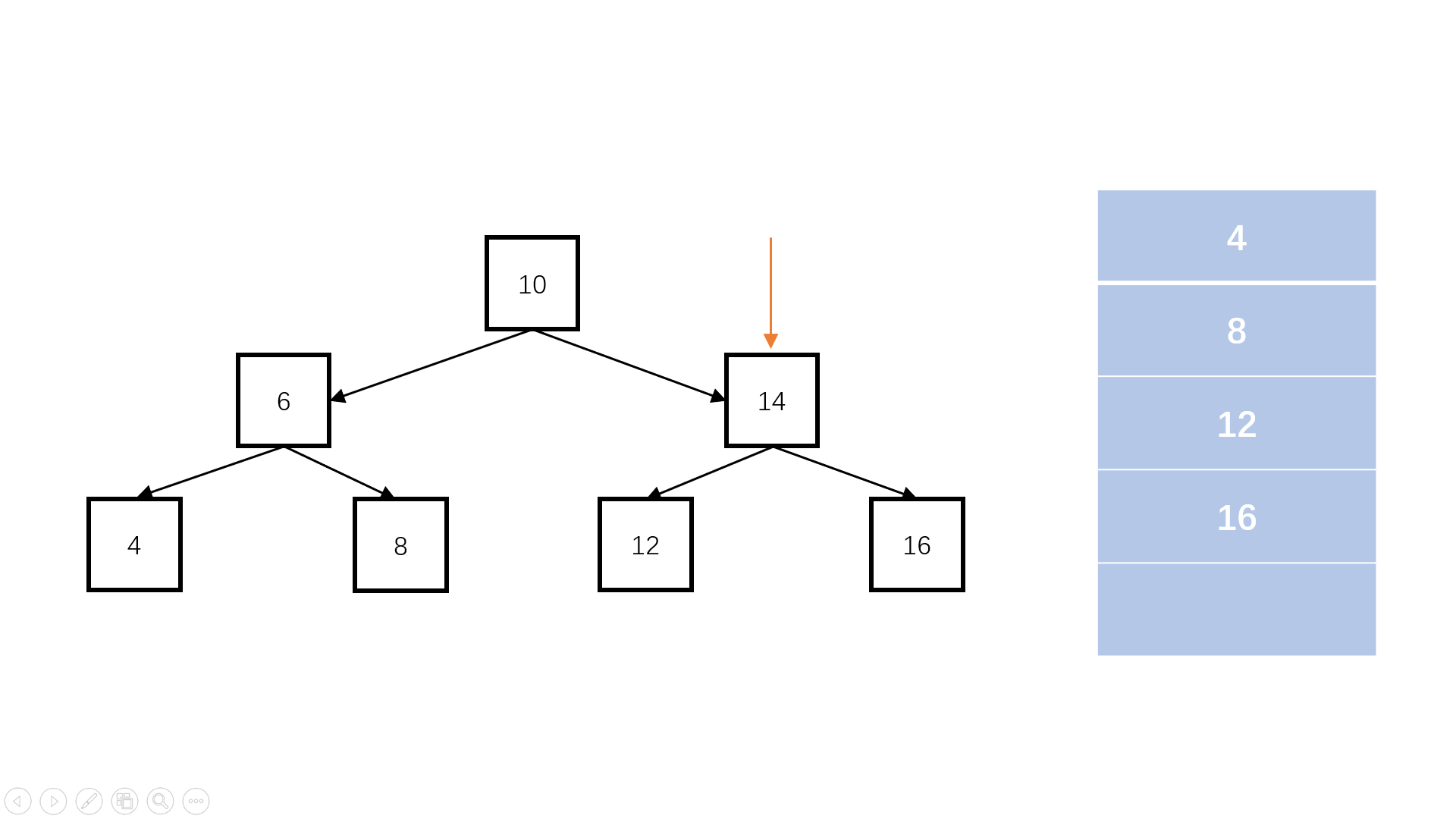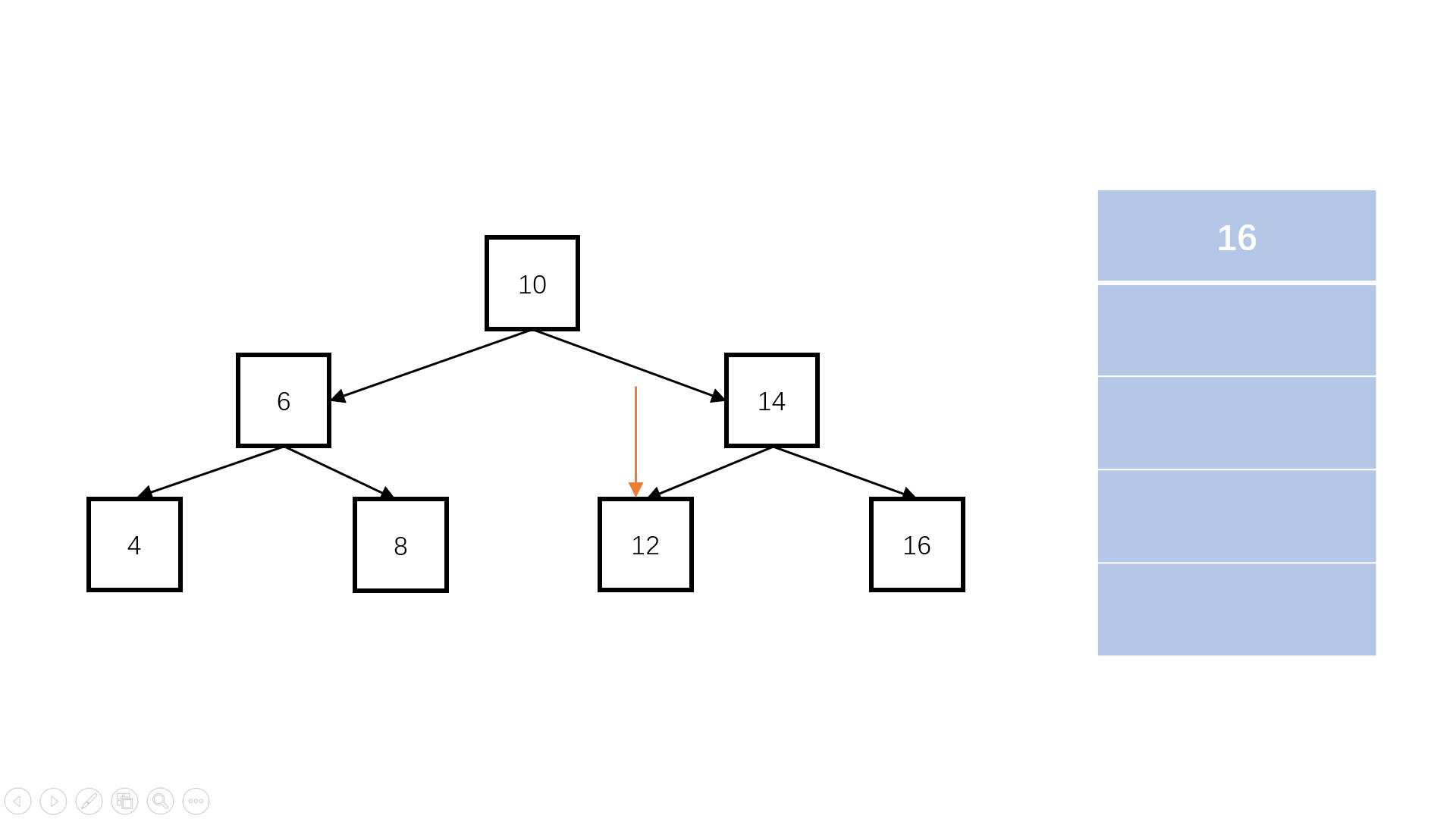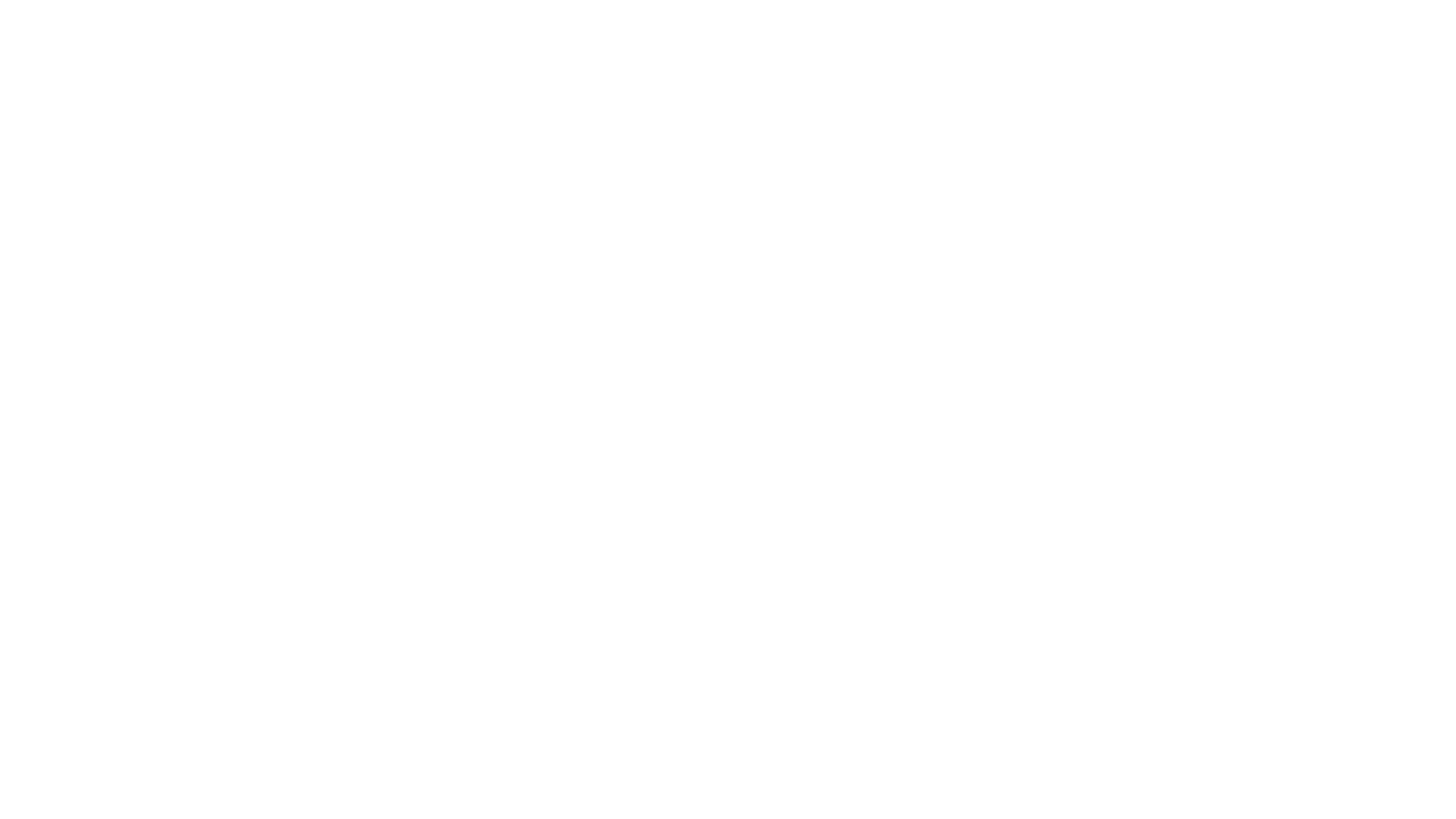
/*
* function TreeNode(x) {
* this.val = x;
* this.left = null;
* this.right = null;
* }
*/
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return bool布尔型
*/
function isCompleteTree(root) {
// write code here
if (root == null) return true;
const queue = [];
queue.push(root);
let flag = false; //是否遇到空节点
while (queue.length) {
const node = queue.shift();
if (node == null) {
//如果遇到某个节点为空,进行标记,代表到了完全二叉树的最下层
flag = true;
continue;
}
if (flag == true) {
//若是后续还有访问,则说明提前出现了叶子节点,不符合完全二叉树的性质。
return false;
}
queue.push(node.left);
queue.push(node.right);
}
return true;
}
module.exports = {
isCompleteTree: isCompleteTree,
};
判断平衡二叉树
平衡二叉树是左子树的高度与右子树的高度差的绝对值小于等于1,同样左子树是平衡二叉树,右子树为平衡二叉树。
递归Math.max(getMaxDepth(root.left)+1,getMaxDepth(root.right)+1)
/* function TreeNode(x) {
this.val = x;
this.left = null;
this.right = null;
} */
function IsBalanced_Solution(pRoot)
{
if(!pRoot) return true;
// write code here
return (Math.abs(getMaxDepth(pRoot.left) - getMaxDepth(pRoot.right)) <=1) && IsBalanced_Solution(pRoot.left) && IsBalanced_Solution(pRoot.right)
}
function getMaxDepth(root) {
if(!root) return 0;
return Math.max(getMaxDepth(root.left)+1,getMaxDepth(root.right)+1)
}
module.exports = {
IsBalanced_Solution : IsBalanced_Solution
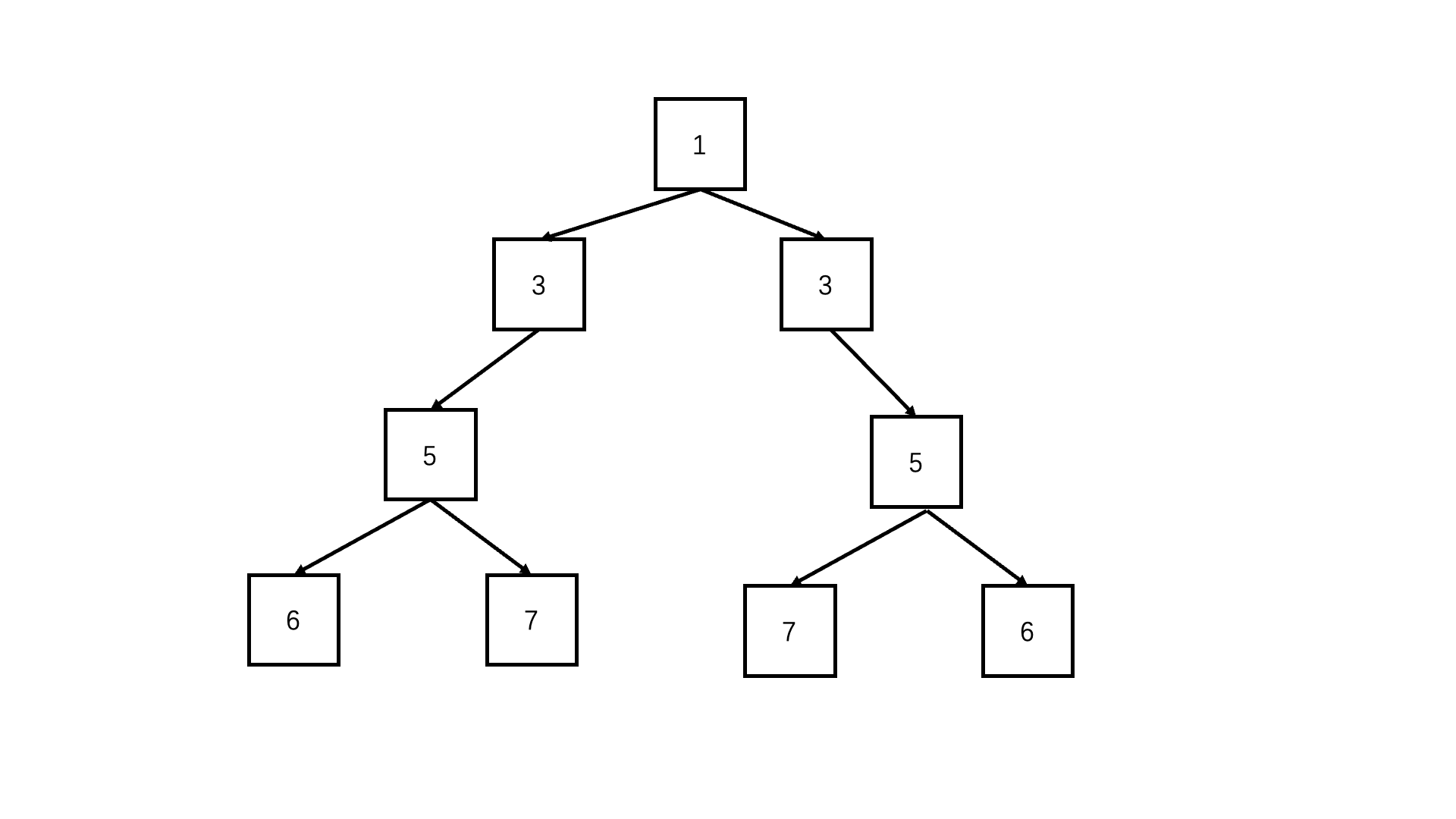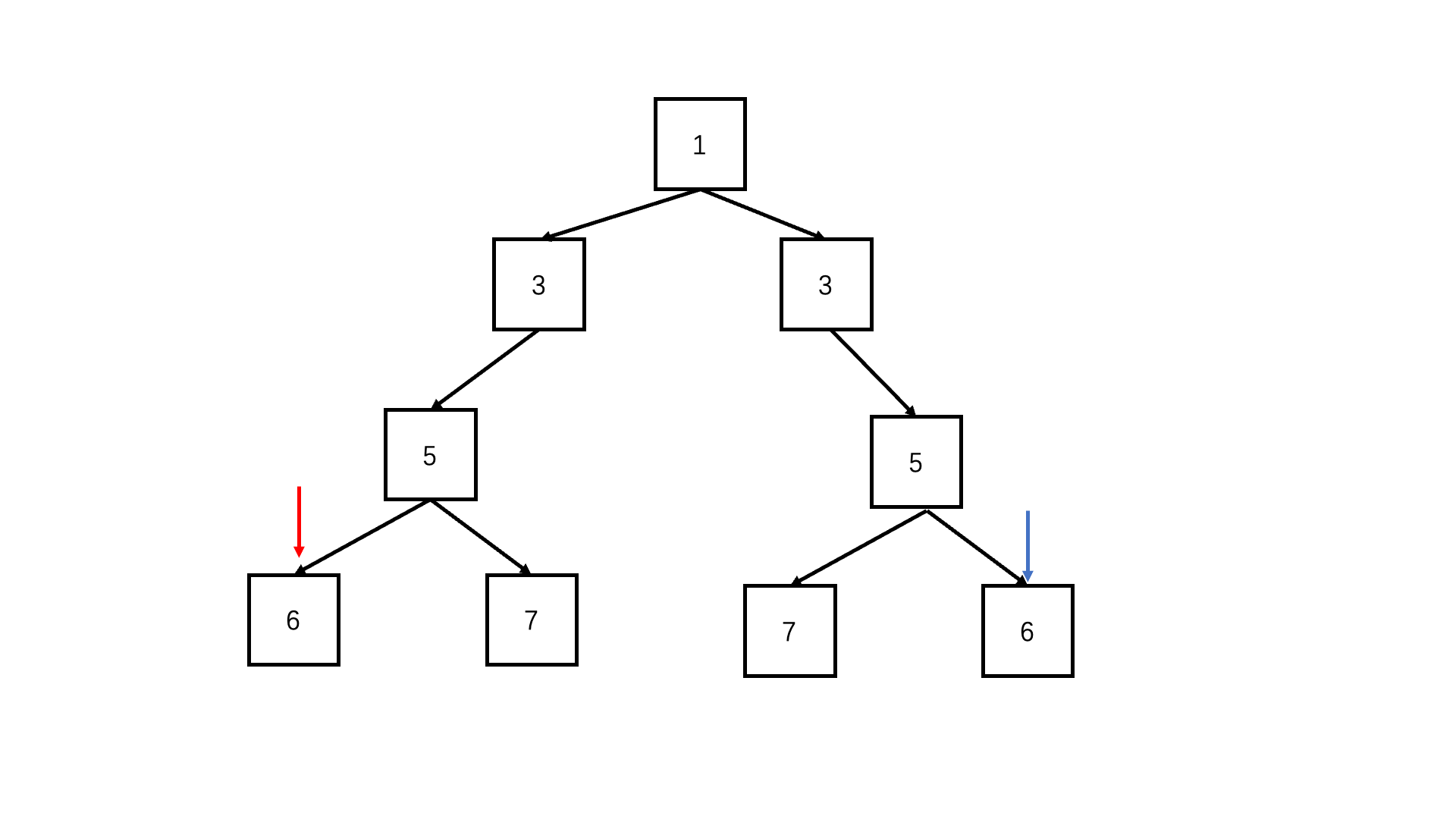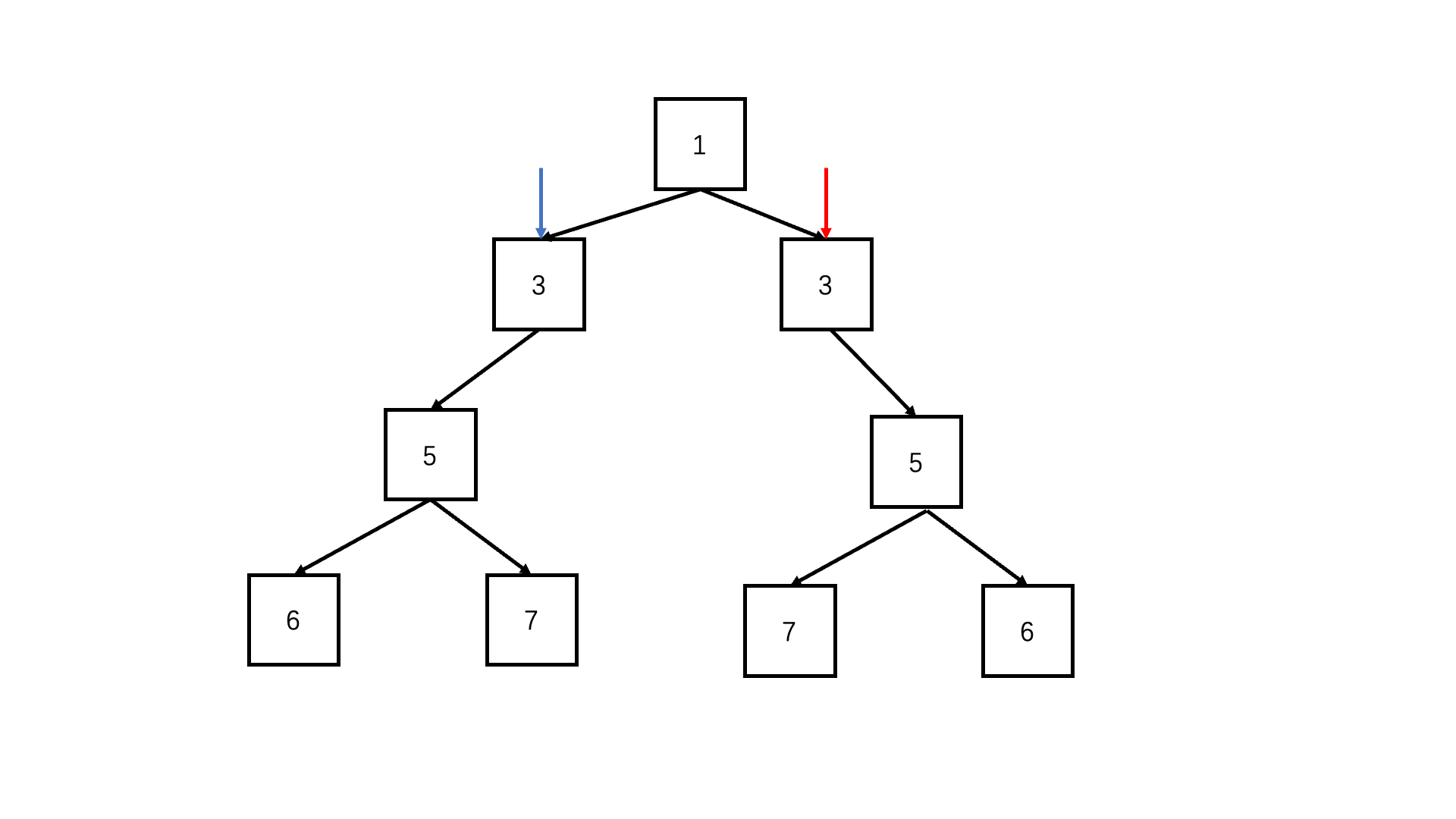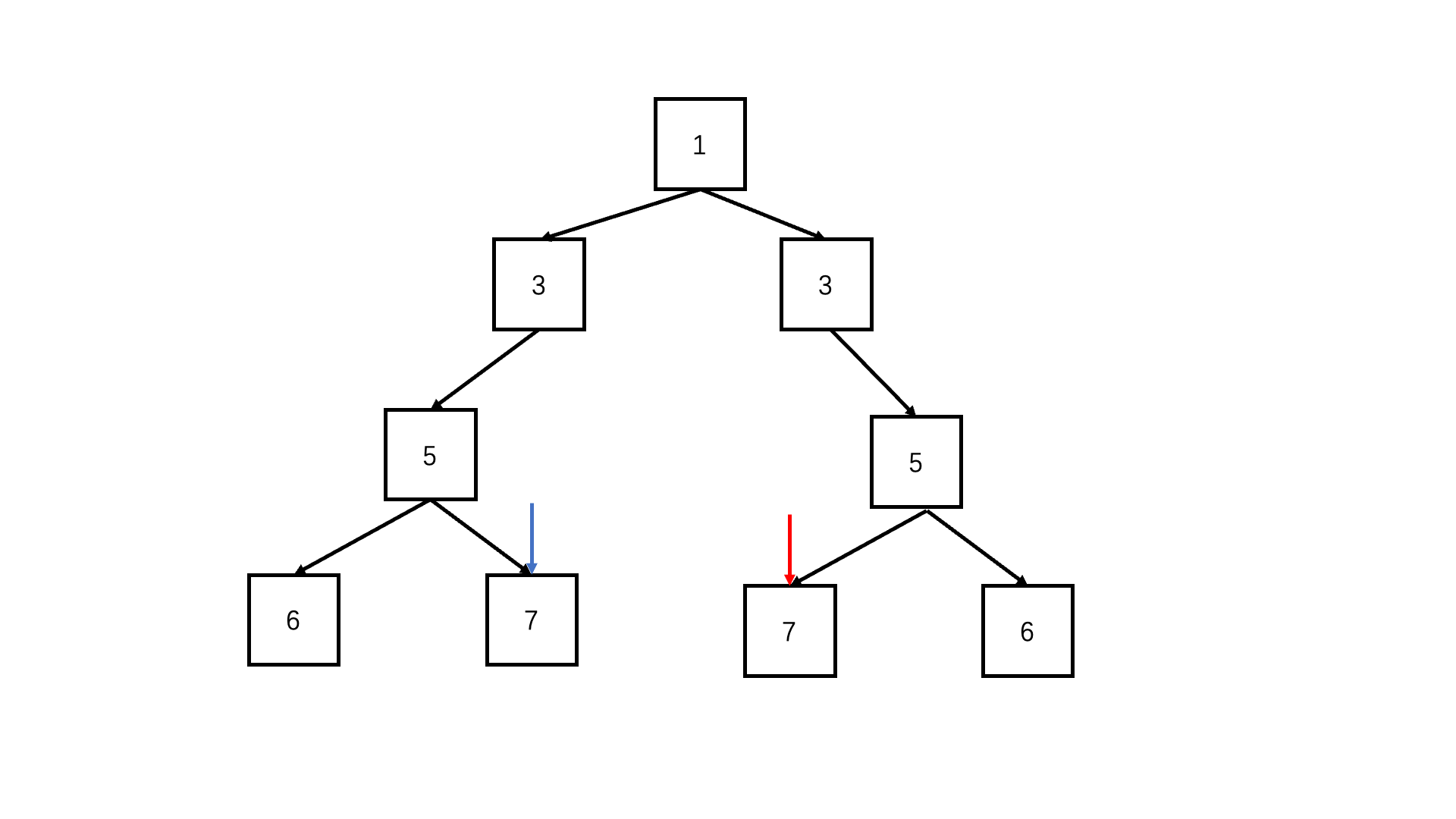
};判断对称二叉树
递归deep(left.left, right.right) && deep(left.right, right.left)
/* function TreeNode(x) {
this.val = x;
this.left = null;
this.right = null;
} */
let flag = true;
function deep(left, right) {
if (!left && !right) return true; //可以两个都为空
if (!right||!left|| left.val !== right.val) {//只有一个为空或者节点值不同,必定不对称
return false;
}
return deep(left.left, right.right) && deep(left.right, right.left); //每层对应的节点进入递归比较
}
function isSymmetrical(pRoot) {
return deep(pRoot, pRoot);
}
module.exports = {
isSymmetrical: isSymmetrical,
};
翻转/生成镜像二叉树
递归交换左右
先序遍历
/*
* function TreeNode(x) {
* this.val = x;
* this.left = null;
* this.right = null;
* }
*/
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pRoot TreeNode类
* @return TreeNode类
*/
function Mirror( pRoot ) {
function traversal(root){
if(root===null) return ;
//交换左右孩子
let temp = root.left;
root.left = root.right;
root.right = temp;
traversal(root.left);
traversal(root.right);
return root;
}
return traversal(pRoot);
// write code here
}
module.exports = {
Mirror : Mirror
};两节点的最近公共祖先
如果从两个节点往上找,每个节点都往上走,一直走到根节点,那么根节点到这两个节点的连线肯定有相交的地方,
如果从上往下走,那么最后一次相交的节点就是他们的最近公共祖先节点。
递归后序遍历
/*
* function TreeNode(x) {
* this.val = x;
* this.left = null;
* this.right = null;
* }
*/
/**
*
* @param root TreeNode类
* @param o1 int整型
* @param o2 int整型
* @return int整型
*/
function dfs(root, o1, o2) {
if (root == null || root.val == o1 || root.val == o2) {
return root;
}
//递归遍历左子树
let left = dfs(root.left, o1, o2);
//递归遍历右子树
let right = dfs(root.right, o1, o2);
//如果left、right都不为空,那么代表o1、o2在root的两侧,所以root为他们的公共祖先
if (left && right) return root;
//如果left、right有一个为空,那么就返回不为空的那一个
return left != null ? left : right;
}构造二叉树
从中序与前/后序遍历序列构造二叉树
//前
var buildTree = function(preorder, inorder) {
if (!preorder.length) return null;
const rootVal = preorder.shift(); // 从前序遍历的数组中获取中间节点的值, 即数组第一个值
const index = inorder.indexOf(rootVal); // 获取中间节点在中序遍历中的下标
const root = new TreeNode(rootVal); // 创建中间节点
root.left = buildTree(preorder.slice(0, index), inorder.slice(0, index)); // 创建左节点
root.right = buildTree(preorder.slice(index), inorder.slice(index + 1)); // 创建右节点
return root;
};
//后
var buildTree = function(inorder, postorder) {
if (!inorder.length) return null;
const rootVal = postorder.pop(); // 从后序遍历的数组中获取中间节点的值, 即数组最后一个值
let rootIndex = inorder.indexOf(rootVal); // 获取中间节点在中序遍历中的下标
const root = new TreeNode(rootVal); // 创建中间节点
root.left = buildTree(inorder.slice(0, rootIndex), postorder.slice(0, rootIndex)); // 创建左节点
root.right = buildTree(inorder.slice(rootIndex + 1), postorder.slice(rootIndex)); // 创建右节点
return root;
};最大二叉树:二叉树的根是数组中的最大元素(递归定义)
var constructMaximumBinaryTree = function (nums) {
const BuildTree = (arr, left, right) => {
if (left > right)
return null;
let maxValue = -1;
let maxIndex = -1;
for (let i = left; i <= right; ++i) {
if (arr[i] > maxValue) {
maxValue = arr[i];
maxIndex = i;
}
}
let root = new TreeNode(maxValue);
root.left = BuildTree(arr, left, maxIndex - 1);
root.right = BuildTree(arr, maxIndex + 1, right);
return root;
}
let root = BuildTree(nums, 0, nums.length - 1);
return root;
};二叉搜索树:左<根<右(按中序遍历有序的树)
删除二叉搜索树中的节点
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} key
* @return {TreeNode}
*/
var deleteNode = function(root, key) {
if (!root) return null;
if (key > root.val) {
root.right = deleteNode(root.right, key);
return root;
} else if (key < root.val) {
root.left = deleteNode(root.left, key);
return root;
} else {
// 场景1: 该节点是叶节点
if (!root.left && !root.right) {
return null
}
// 场景2: 有一个孩子节点不存在
if (root.left && !root.right) {
return root.left;
} else if (root.right && !root.left) {
return root.right;
}
// 场景3: 左右节点都存在
const rightNode = root.right;
// 获取最小值节点
const minNode = getMinNode(rightNode);
// 将待删除节点的值替换为最小值节点值
root.val = minNode.val;
// 删除最小值节点
root.right = deleteNode(root.right, minNode.val);
return root;
}
};
function getMinNode(root) {
while (root.left) {
root = root.left;
}
return root;
}修剪二叉搜索树
修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L)
var trimBST = function (root,low,high) {
if(root === null) {
return null;
}
if(root.val < low) {
let right = trimBST(root.right, low, high);
return right;
}
if(root.val > high) {
let left = trimBST(root.left, low, high);
return left;
}
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root;
}有序数组转换为平衡二叉搜索树
left, right比arr.slice高效
Math.floor(left + (right - left) / 2)
var sortedArrayToBST = function (nums) {
const buildTree = (Arr, left, right) => {
if (left > right)
return null;
let mid = Math.floor(left + (right - left) / 2);
let root = new TreeNode(Arr[mid]);
root.left = buildTree(Arr, left, mid - 1);
root.right = buildTree(Arr, mid + 1, right);
return root;
}
return buildTree(nums, 0, nums.length - 1);
};最值、差值->有序数组的差值、最值
二叉搜索树的最小绝对差
二叉搜索树转换为累加树
一个有序数组[2, 5, 13],求从后到前的累加数组,也就是[20, 18, 13]
累加的顺序是右中左,所以我们需要反中序遍历这个二叉树,然后顺序累加
’东哥带你刷二叉树(思路篇) | labuladong 的算法笔记