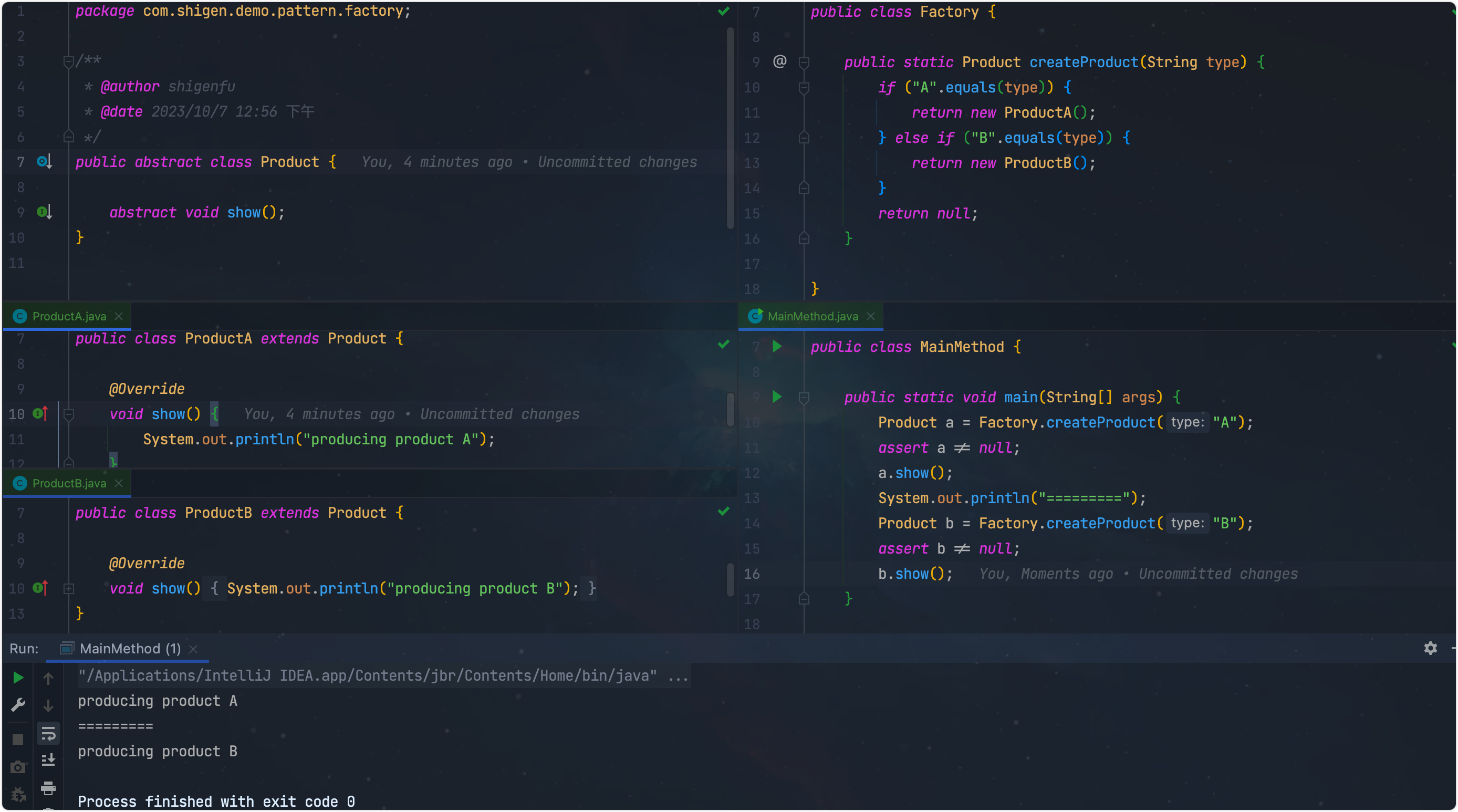
单目相机通过对极约束来求解相机运动的位姿。参考了ORBSLAM中单目实现的代码,这里用opencv来实现最简单的位姿估计.

mLeftImg = cv::imread(lImg, cv::IMREAD_GRAYSCALE);
mRightImg = cv::imread(rImg, cv::IMREAD_GRAYSCALE);
cv::Ptr<ORB> OrbLeftExtractor = cv::ORB::create();
cv::Ptr<ORB> OrbRightExtractor = cv::ORB::create();
OrbLeftExtractor->detectAndCompute(mLeftImg, noArray(), mLeftKps, mLeftDes);
OrbRightExtractor->detectAndCompute(mRightImg, noArray(), mRightKps, mRightDes);
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create(DescriptorMatcher::BRUTEFORCE_HAMMING);
matcher->match(mLeftDes, mRightDes, mMatches);首先通过ORB特征提取,获取两幅图像的匹配度,我将其连线出来的效果:

RANSAC的算法原理可以google,很容易理解。先看看ORBSLAM中的实现:
bool Initializer::Initialize(const Frame &CurrentFrame, const vector<int> &vMatches12, cv::Mat &R21, cv::Mat &t21,
vector<cv::Point3f> &vP3D, vector<bool> &vbTriangulated)
{
// Fill structures with current keypoints and matches with reference frame
// Reference Frame: 1, Current Frame: 2
// Frame2 特征点
mvKeys2 = CurrentFrame.mvKeysUn;
// mvMatches12记录匹配上的特征点对
mvMatches12.clear();
mvMatches12.reserve(mvKeys2.size());
// mvbMatched1记录每个特征点是否有匹配的特征点,
// 这个变量后面没有用到,后面只关心匹配上的特征点
mvbMatched1.resize(mvKeys1.size());
// 步骤1:组织特征点对
for(size_t i=0, iend=vMatches12.size();i<iend; i++)
{
if(vMatches12[i]>=0)
{
mvMatches12.push_back(make_pair(i,vMatches12[i]));
mvbMatched1[i]=true;
}
else
mvbMatched1[i]=false;
}
// 匹配上的特征点的个数
const int N = mvMatches12.size();
// Indices for minimum set selection
// 新建一个容器vAllIndices,生成0到N-1的数作为特征点的索引
vector<size_t> vAllIndices;
vAllIndices.reserve(N);
vector<size_t> vAvailableIndices;
for(int i=0; i<N; i++)
{
vAllIndices.push_back(i);
}
// Generate sets of 8 points for each RANSAC iteration
// **步骤2:在所有匹配特征点对中随机选择8对匹配特征点为一组,共选择mMaxIterations组 **
// 用于FindHomography和FindFundamental求解
// mMaxIterations:200
mvSets = vector< vector<size_t> >(mMaxIterations,vector<size_t>(8,0));
DUtils::Random::SeedRandOnce(0);
for(int it=0; it<mMaxIterations; it++)
{
vAvailableIndices = vAllIndices;
// Select a minimum set
for(size_t j=0; j<8; j++)
{
// 产生0到N-1的随机数
int randi = DUtils::Random::RandomInt(0,vAvailableIndices.size()-1);
// idx表示哪一个索引对应的特征点被选中
int idx = vAvailableIndices[randi];
mvSets[it][j] = idx;
// randi对应的索引已经被选过了,从容器中删除
// randi对应的索引用最后一个元素替换,并删掉最后一个元素
vAvailableIndices[randi] = vAvailableIndices.back();
vAvailableIndices.pop_back();
}
}
// Launch threads to compute in parallel a fundamental matrix and a homography
// 步骤3:调用多线程分别用于计算fundamental matrix和homography
vector<bool> vbMatchesInliersH, vbMatchesInliersF;
float SH, SF; // score for H and F
cv::Mat H, F; // H and F
// ref是引用的功能:http://en.cppreference.com/w/cpp/utility/functional/ref
// 计算homograpy并打分
thread threadH(&Initializer::FindHomography,this,ref(vbMatchesInliersH), ref(SH), ref(H));
// 计算fundamental matrix并打分
thread threadF(&Initializer::FindFundamental,this,ref(vbMatchesInliersF), ref(SF), ref(F));
// Wait until both threads have finished
threadH.join();
threadF.join();
// Compute ratio of scores
// 步骤4:计算得分比例,选取某个模型
float RH = SH/(SH+SF);
// Try to reconstruct from homography or fundamental depending on the ratio (0.40-0.45)
// 步骤5:从H矩阵或F矩阵中恢复R,t
if(RH>0.40)
return ReconstructH(vbMatchesInliersH,H,mK,R21,t21,vP3D,vbTriangulated,1.0,50);
else //if(pF_HF>0.6)
return ReconstructF(vbMatchesInliersF,F,mK,R21,t21,vP3D,vbTriangulated,1.0,50);
return false;
}
orbslam首先是从配对特征中随机迭代mMaxIterations次,每一次都从配对点中选出8个点用来计算homography和fundamental矩阵,都是用SVD来计算的,如下:
FindFundamental:
void Initializer::FindFundamental(vector<bool> &vbMatchesInliers, float &score, cv::Mat &F21)
{
// Number of putative matches
const int N = vbMatchesInliers.size();
// 分别得到归一化的坐标P1和P2
vector<cv::Point2f> vPn1, vPn2;
cv::Mat T1, T2;
Normalize(mvKeys1,vPn1, T1);
Normalize(mvKeys2,vPn2, T2);
cv::Mat T2t = T2.t();
// Best Results variables
score = 0.0;
vbMatchesInliers = vector<bool>(N,false);
// Iteration variables
vector<cv::Point2f> vPn1i(8);
vector<cv::Point2f> vPn2i(8);
cv::Mat F21i;
vector<bool> vbCurrentInliers(N,false);
float currentScore;
// Perform all RANSAC iterations and save the solution with highest score
for(int it=0; it<mMaxIterations; it++)
{
// Select a minimum set
for(int j=0; j<8; j++)
{
int idx = mvSets[it][j];
vPn1i[j] = vPn1[mvMatches12[idx].first];
vPn2i[j] = vPn2[mvMatches12[idx].second];
}
cv::Mat Fn = ComputeF21(vPn1i,vPn2i);
F21i = T2t*Fn*T1; //解除归一化
// 利用重投影误差为当次RANSAC的结果评分
currentScore = CheckFundamental(F21i, vbCurrentInliers, mSigma);
if(currentScore>score)
{
F21 = F21i.clone();
vbMatchesInliers = vbCurrentInliers;
score = currentScore;
}
}
}通过ComputeF21计算本质矩阵,
cv::Mat Initializer::ComputeF21(const vector<cv::Point2f> &vP1,const vector<cv::Point2f> &vP2)
{
const int N = vP1.size();
cv::Mat A(N,9,CV_32F); // N*9
for(int i=0; i<N; i++)
{
const float u1 = vP1[i].x;
const float v1 = vP1[i].y;
const float u2 = vP2[i].x;
const float v2 = vP2[i].y;
A.at<float>(i,0) = u2*u1;
A.at<float>(i,1) = u2*v1;
A.at<float>(i,2) = u2;
A.at<float>(i,3) = v2*u1;
A.at<float>(i,4) = v2*v1;
A.at<float>(i,5) = v2;
A.at<float>(i,6) = u1;
A.at<float>(i,7) = v1;
A.at<float>(i,8) = 1;
}
cv::Mat u,w,vt;
cv::SVDecomp(A,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
cv::Mat Fpre = vt.row(8).reshape(0, 3); // v的最后一列
cv::SVDecomp(Fpre,w,u,vt,cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
w.at<float>(2)=0; // 秩2约束,将第3个奇异值设为0 //强迫约束
return u*cv::Mat::diag(w)*vt;
}
看到用的是线性SVD解。
通过重投影来评估本质矩阵的好坏。
float Initializer::CheckFundamental(const cv::Mat &F21, vector<bool> &vbMatchesInliers, float sigma)
{
const int N = mvMatches12.size();
const float f11 = F21.at<float>(0,0);
const float f12 = F21.at<float>(0,1);
const float f13 = F21.at<float>(0,2);
const float f21 = F21.at<float>(1,0);
const float f22 = F21.at<float>(1,1);
const float f23 = F21.at<float>(1,2);
const float f31 = F21.at<float>(2,0);
const float f32 = F21.at<float>(2,1);
const float f33 = F21.at<float>(2,2);
vbMatchesInliers.resize(N);
float score = 0;
// 基于卡方检验计算出的阈值(假设测量有一个像素的偏差)
const float th = 3.841; //置信度95%,自由度1
const float thScore = 5.991;//置信度95%,自由度2
const float invSigmaSquare = 1.0/(sigma*sigma);
for(int i=0; i<N; i++)
{
bool bIn = true;
const cv::KeyPoint &kp1 = mvKeys1[mvMatches12[i].first];
const cv::KeyPoint &kp2 = mvKeys2[mvMatches12[i].second];
const float u1 = kp1.pt.x;
const float v1 = kp1.pt.y;
const float u2 = kp2.pt.x;
const float v2 = kp2.pt.y;
// Reprojection error in second image
// l2=F21x1=(a2,b2,c2)
// F21x1可以算出x1在图像中x2对应的线l
const float a2 = f11*u1+f12*v1+f13;
const float b2 = f21*u1+f22*v1+f23;
const float c2 = f31*u1+f32*v1+f33;
// x2应该在l这条线上:x2点乘l = 0
const float num2 = a2*u2+b2*v2+c2;
const float squareDist1 = num2*num2/(a2*a2+b2*b2); // 点到线的几何距离 的平方
const float chiSquare1 = squareDist1*invSigmaSquare;
if(chiSquare1>th)
bIn = false;
else
score += thScore - chiSquare1;
// Reprojection error in second image
// l1 =x2tF21=(a1,b1,c1)
const float a1 = f11*u2+f21*v2+f31;
const float b1 = f12*u2+f22*v2+f32;
const float c1 = f13*u2+f23*v2+f33;
const float num1 = a1*u1+b1*v1+c1;
const float squareDist2 = num1*num1/(a1*a1+b1*b1);
const float chiSquare2 = squareDist2*invSigmaSquare;
if(chiSquare2>th)
bIn = false;
else
score += thScore - chiSquare2;
if(bIn)
vbMatchesInliers[i]=true;
else
vbMatchesInliers[i]=false;
}
return score;
}最后回到Initializer::Initialize,将单映矩阵和本质矩阵的得分进行比对,选出最合适的,就求出RT了。
ORBSLAM2同时考虑了单应和本质,SLAM14讲中也说到,工程实践中一般都讲两者都计算出来选择较好的,不过效率上会影响比较多感觉。
opencv实现就比较简单了,思路和上面的类似,只是现在只考虑本质矩阵。在之前获取到特征点之后,
/*add ransac method for accurate match*/
vector<Point2f> vLeftP2f;
vector<Point2f> vRightP2f;
for(auto& each:mMatches)
{
vLeftP2f.push_back(mLeftKps[each.queryIdx].pt);
vRightP2f.push_back(mRightKps[each.trainIdx].pt);
}
vector<unsigned char> vTemp(vLeftP2f.size());
/*计算本质矩阵,用RANSAC*/
Mat transM = findEssentialMat(vLeftP2f, vRightP2f, cameraMatrix,RANSAC, 0.999, 1.0, vTemp);
vector<DMatch> optimizeM;
for(int i = 0; i < vTemp.size(); i++)
{
if(vTemp[i])
{
optimizeM.push_back(mMatches[i]);
}
}
mMatches.swap(optimizeM);
cout << transM<<endl;
Mat optimizeP;
drawMatches(mLeftImg, mLeftKps, mRightImg, mRightKps, mMatches, optimizeP);
imshow("output5", optimizeP);看下结果:

确实效果好多了,匹配准确度比之前的要好,之后我们就可以通过这个本质矩阵来计算RT了。
Mat R, t, mask;
recoverPose(transM, vLeftP2f, vRightP2f, cameraMatrix, R, t, mask);一个接口搞定。最后我们可以通过验证对极约束,来看看求出的位姿是否准确。
定义检查函数:
Mat cameraMatrix = (Mat_<double>(3,3) << CAM_FX, 0.0, CAM_CX, 0.0, CAM_FY, CAM_CY, 0.0, 0.0, 1.0);
bool epipolarConstraintCheck(Mat CameraK, vector<Point2f>& p1s, vector<Point2f>& p2s, Mat R, Mat t)
{
for(int i = 0; i < p1s.size(); i++)
{
Mat y1 = (Mat_<double>(3,1)<<p1s[i].x, p1s[i].y, 1);
Mat y2 = (Mat_<double>(3,1)<<p2s[i].x, p2s[i].y, 1);
//T 的凡对称矩阵
Mat t_x = (Mat_<double>(3,3)<< 0, -t.at<double>(2,0), t.at<double>(1,0),
t.at<double>(2,0), 0, -t.at<double>(0,0),
-t.at<double>(1,0),t.at<double>(0,0),0);
Mat d = y2.t() * cameraMatrix.inv().t() * t_x * R * cameraMatrix.inv()* y1;
cout<<"epipolar constraint = "<<d<<endl;
}
}最后可以看到结果都是趋近于0的,证明位姿还是比较准确的。