图的存储-链式前向星

news2024/11/24 12:25:14

链式前向星

链式前向星是民间OI选手发明的数据结构。用另一个词解释它就是：用数组模拟的邻接链表。最核心的思想就是用数组模拟链表。

（1）前向星

前向星就是边的集合。一个图，只要将它的所有边存储起来，就能知道它的所有信息。但是前向星对于边的存储做了一些排序。

假设有如下图：输入a->b，有一条a指向b的边。

对于边的起点排序：

编号:     1      2      3      4      5      6      7

起点u:    1      1      1      2      3      4      4
终点v:    2      3      5      3      4      1      5

如果用前向星存图，至少需要三个数组：边的数组，起点开始位置的数组，起点终点位置的数组。并且还涉及边的排序，比较麻烦。

（2）链式前向星

链式前向星摒弃了排序，采用链表思想存储同一个起点的边，又为了避免链表结构的臃肿，利用数组模拟链表。

同样需要三个数组：边的数组edge、起点的第一条边位置的数组head、每条边相同起点的下一条边位置的数组next

edge【i】存储的是第i条边；
head【i】表示以节点序号i为起点的第一条边存储位置；
next【i】表示第i条边的下一条边，要求下一条边与这条边同起点。

注意：

上述声明涉及两种序号概念——节点的序号和边的序号！边的序号由输入顺序给定，节点的序号用来区分节点。

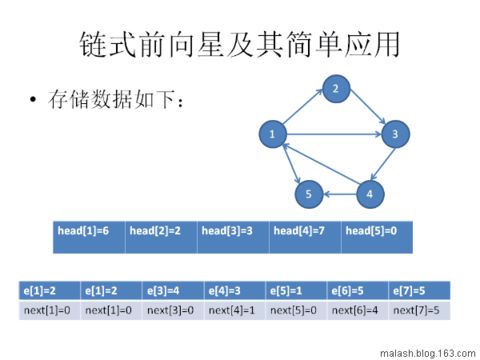
极端优化：由于head【i】已经知道边的起点，所以edge【i】也没必要存边的起点，直接存边的终点。这样，假设无权图输入都是整数，我们只需要三个一维整数数组就能存储整个图！

对于有权图的情况，edge【i】需要额外存储边的权值。参考博客

（3）应用

输入每条边，然后按起点顺序输出每条边。

public class Main {
    public static void main(String[] args) throws InterruptedException{
        Scanner cin = new Scanner(System.in);
        int N = cin.nextInt(); //N个顶点
        int M = cin.nextInt(); //M条边
        int[] edge = new int[M];
        int[] head = new int[N+1]; //节点编号从1开始
        int[] next = new int[M];
        Arrays.fill(head, -1); //-1作为链表的结束标志
        // 输入
        for(int i=0; i<M; ++i){
            // 输入一条边 a->b
            cin.nextLine();
            int a = cin.nextInt();
            int b = cin.nextInt();
            // 存入三个数组中
            edge[i] = b;
            next[i] = head[a];
            head[a] = i;
        }
        // 输出：遍历每个起点的边
        for(int i=1; i<=N; ++i){
            int start = head[i];
            while(start!=-1){
                System.out.println(i+"->"+edge[start]);
                start = next[start];
            }
        }
    }
}