目录
前言
01背包问题
问题描述
编辑
动态规划
基本概念
怎么理解动态规划?
解决01背包问题
代码实现
前言
今天我们学习一种新的算法---动态规划，这种算法思想是属于枚举的一种，下面我就通过01背包问题来说明这种算法的解决思路。
01背包问题
问题描述
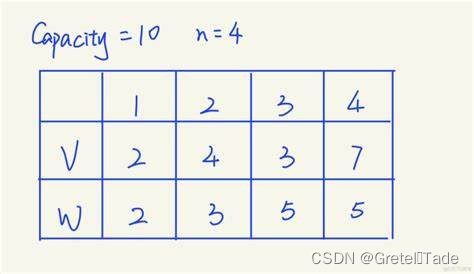
现在有n个物品，它们有各自的体积和价值，然后通过一定容量capacity的背包去装这些物品，问怎么去装实现价值最大化？
图示如下：
动态规划
基本概念
动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。
以上定义来自维基百科，看定义感觉还是有点抽象。简单来说，动态规划其实就是，给定一个问题，我们把它拆成一个个子问题，直到子问题可以直接解决。然后呢，把子问题答案保存起来，以减少重复计算。再根据子问题答案反推，得出原问题解的一种方法。
怎么理解动态规划?
举个例子，1+1+1+1+1=？，很显然答案是5，好那我要算出6怎么去算呢？那就在5的基础上再+1就行了，这就是动态规划的表现，也就是说我前面需要一个东西来标记我前面算出来的值，然后后面要进一步去算的时候就只需要把这个值拿过来用就行了，不需要去重新算，这就是动态规划。
解决01背包问题
当我们看到01背包问题的时候，我们可能会去一个一个列举，然后找到最优解，在列举的过程中你是否发现一些规律呢？也就是当我们列举了前面一些情况的时候，再去列举后面的其他情况就没必要去重新思考前面的东西，也就是说我们可以通过前面的直接去递推后面的即可。这就是动态规划的精髓所在。下面我就详细说明通过动态规划来解决这个问题的过程。
为了方面说明，下面定义一些量：
1、i表示第i个物品；
2、v(i)表示第i个物品的价值；
3、w(i)表示第i个物品的重量（容量）；
4、V(i,j) 表示当背包容量为j的时候，能最大装下前i个物品整体的最大价值
这么来说的话，我们只需要去找到所有的V(0,0)~V(i,j) 情况即可，然后列举出来就知道最优解。
当前会发现有两种递推规律：
1、如果当前容量j过于小的话，即使增加一个物品i的范围也无法装下，那么当前价值还是前i-1个物品的价值，也就是V(i,j)=V(i-1,j)
2.如果当前容量j能装下当前增加范围的物品话，即使能装下但不一定是最佳情况，那么我们要去与前面情况V(i-1,j)进行比较，也就是V(i,j)=max{V(i-1,j) , V(i,j-w(i))+v(i)}
- j<w(i) V(i,j)=V(i-1,j)
- j>=w(i) V(i,j)=max｛V(i-1,j)，V(i-1,j-w(i))+v(i)｝
通过以上的规律，我们就可以去做出一张表来，i和j都从0开始，如下图所示：
然后就是填表环节，比如：i=1，j=1的时候，V(1,1)=V(1-1,1)=V(0,1)=0；当i=2，j=2的时候，V(2,2)=max{V(1,2),V(2,2-2)+v(2)}，结果就是2，以此类推……
填表结果如下：
可以看，最大容纳价值就是V(4,9)=13
代码实现
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
//比较二者返回最大值
int max(int a, int b) {
return a > b ? a : b;
}
//输出结果
void print(int** table, int line, int bag_c,int* judge) {
for (int x = 0; x < line; x++) {
for (int y = 0; y < bag_c + 1; y++) {
printf("%-3d ", table[x][y]);
}
puts("");
}
printf("\n当背包容量为%d的时候，最大容纳价值:%d\n", bag_c, table[line-1][bag_c]);
}
//填表操作
void build_table(int* val,int* weight,int** table,int bag_j,int line,int* judge)
{
for (int x = 1; x < line; x++) {
for (int j = 1; j < bag_j + 1; j++) {
if (j < weight[x])//如果当前背包的容量无法装下多余的物品时候，那么价值还是上一个的价值
table[x][j] = table[x - 1][j];
else {//如果能装下，那就比较装下之后和之前的价值,取最大
table[x][j] = max(table[x - 1][j], table[x - 1][j - weight[x]] + val[x]);
if (table[x][j] != table[x - 1][j])
judge[x] = table[x][j];
}
}
}
}
int main() {
int bag_j;
printf("输入你的背包容量：");
scanf("%d", &bag_j);
//当前背包的价值以及对应的重量
int value[] = { 0,2,4,3,7 };
int weight[] = { 0,2,3,5,5 };
int line = sizeof(value) / sizeof(int);//表格的行数
int* judge = (int*)malloc(sizeof(int) * line);
int** table = (int**)malloc(sizeof(int*) * line);
for (int k = 0; k < line; k++) {
table[k] = (int*)malloc(sizeof(int) * (bag_j + 1));
}
for (int i = 0; i < line; i++) {
for (int j = 0; j < bag_j + 1; j++) {
table[i][j] = 0;//表格数据初始化为0
}
}
memset(judge, 0, sizeof(judge));//初始化
build_table(value, weight, table, bag_j, line,judge);
print(table, line, bag_j,judge);
}
结果如下：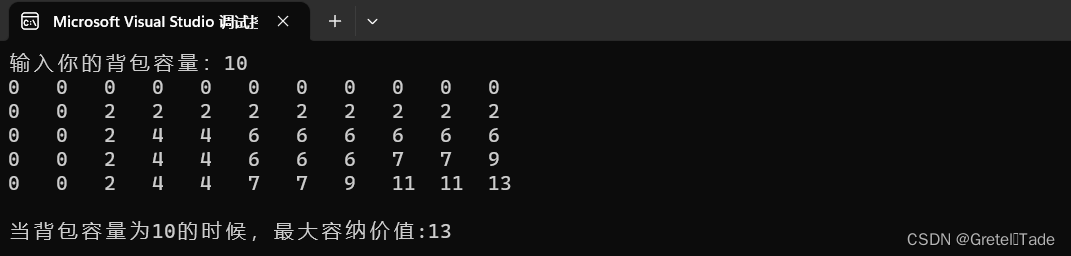
以上就是本期的全部内容了，我们下一期再见！
分享一张壁纸：
