URL：https://atcoder.jp/contests/abc297

目录

F

Problem/题意

Thought/思路

Code/代码

---

F

Problem/题意

给一个 H * W 的矩形，在其中任意放置 K 个点，由这 K 个点构成的最小矩形带来的贡献为该矩形的面积，这 K 个点构成一种方案。

问面积的期望（总面积 / 总方案数）。

Thought/思路

很容易发现，对于这个 H * W 的矩形而言，总方案数为：。也就是说，我们只需要求出总面积即可。

对于某个最小矩形，构成它的摆放方法有很多种，也就是说，如果我们能算出一个大小为 i * j 的矩形，他有 X 种合法的摆放方案，再用合法方案数乘上该矩形的面积（即 X * i * j），就是对应的贡献。

问题就在于如何求出一个大小为 i * j 的矩形有多少种合法摆法：应用容斥原理。

---

简单说一下容斥原理：合法方案 = 总方案 - 非法方案。对于几个集合，求他们的并集，就应用到容斥原理：加上奇数个集合的交集，减去偶数个集合的交集。

https://blog.csdn.net/Annabel_CM/article/details/110285940

---

对于一个 i * j 的矩形，很容易求出总方案数，那么问题就在于求出非法方案数。

先看非法情况下的矩形有：C1、C2、C3、C4

所以现在的目的就明确了，求出 C1、C2、C3、C4 的并集，得到非法方案数，再用 i * j 的总方案数减去非法方案数，就能算出合法方案数。

那么怎么求它们的并集呢？

---

 上面的写法中，C0 代表总方案数，[ ] 里的内容就是非法方案数。我们对每一类交集举例说明：

（1）C1： 或 

（2）C1 & C2：；

（3）C1 & C3：；

（4）C1 & C2 & C3：；

（5）C2 & C3 & C4：；

（6）C1 & C2 & C3 & C4：；

把上面手写的图片中的内容，用这 6 种情况依次替换，合并同类项，就能得到下列式子：

（cnt：就是组合数 C）

---

接下来还剩最后一个部分，对于我们上面求出来的一种矩形的的有效摆放方法，在 H * W 中又能摆在多少个位置呢？

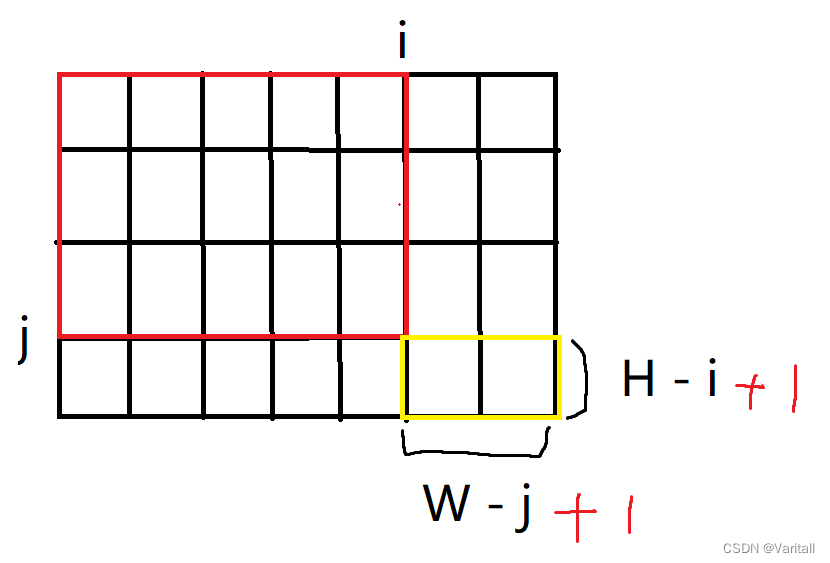
只需要把 i、j 距离 H、W 的距离 + 1，然后相乘，就是 i * j 这个矩形能摆放的位置数：

(H - i + 1) * (W - j + 1)

---

位置数 * 矩形面积（i * j）* 合法方案数，就是一个矩形 i * j 带来的贡献，遍历 H、W，求出每一种（i，j）的贡献，累加，就是最后的总贡献。

Code/代码

#include "bits/stdc++.h"

#define int long long

const int mod = 998244353;

int h, w, k, fact[1000007], invf[1000007];

int ksm(int a, int b) {
	int res = 1;
	while (b > 0) {
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b /= 2;
	}
	return res;
}

int C(int x, int y) {
	if (x < y) return 0;
	return fact[x] * invf[y] % mod * invf[x - y] % mod;
}

signed main() {
	std::cin >> h >> w >> k;

	if (k == 1) {
		std::cout << 1;
		return 0;
	}

	fact[0] = 1;
	invf[0] = ksm(fact[0], mod - 2);
	for (int i = 1; i <= 1000005; ++ i) {
		fact[i] = fact[i - 1] * i % mod;
		invf[i] = ksm(fact[i], mod - 2) % mod;
	}

	int ans = 0;
	for (int i = 1; i <= h; ++ i) {
		for (int j = 1; j <= w; ++ j) {
			int cnt = 0;
			for (int x = 0; x <= 2; ++ x) {
				for (int y = 0; y <= 2; ++ y) {
					cnt = (cnt + C((i - x) * (j - y), k) * (x == 1 ? -2 : 1) * (y == 1 ? -2 : 1) % mod + mod) % mod;
				}
			}
			ans = (ans + i * j % mod * (h - i + 1) % mod * (w - j + 1) % mod * cnt % mod + mod) % mod;
		}
	}

	std::cout << ans * ksm(C(h * w, k), mod - 2) % mod;
}