第三章
Q1: 
A1:(1) 原码:
[
−
(
2
63
−
1
,
2
63
−
1
]
[-(2^{63}-1,2^{63}-1]
[−(263−1,263−1] 补码:
[
−
(
2
63
,
2
63
−
1
]
[-(2^{63},2^{63}-1]
[−(263,263−1]
补充:

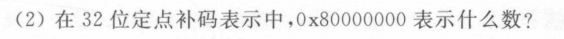
A2:
−
2
31
-2^{31}
−231
【方法–将非符号位取反,末位+1,再根据符号位得到机器数】
补码补充:
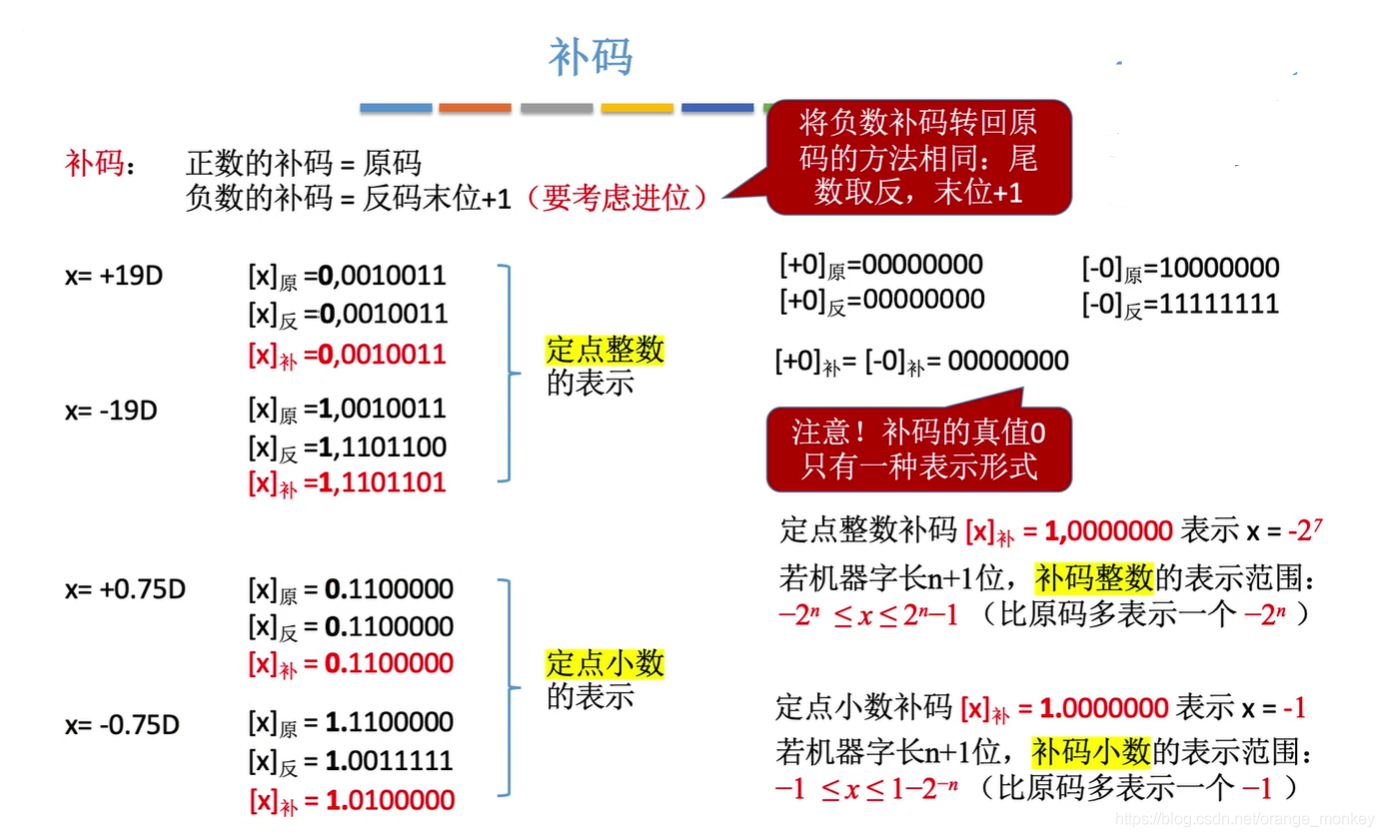
Q2:

A2:
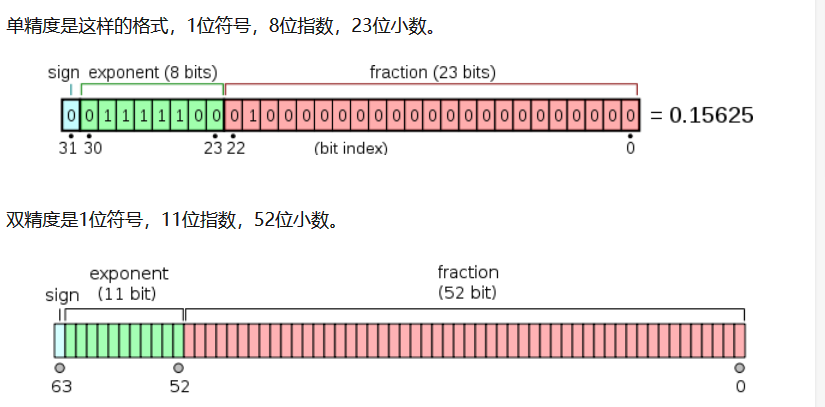
单精度和双精度精确的范围不一样
- 单精度,也即float,一般在计算机中存储占用4字节,也32位,有效位数为7位;
- 双精度(double)在计算机中存储占用8字节,64位,有效位数为16位。
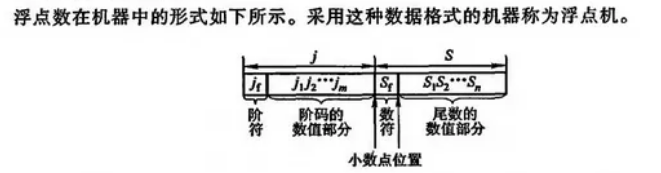
浮点数
- 1.00e+02表示1.00*(10^2)
2.34e-03表示2.34*(10^-3)
在一些数学软件中,这个e表示10,后面+02表示10的次方数。
(1) 【单精度】0x7ff0000= 0,0000 1111, 111 1111 0000 0000 0000 0000=
(
1.1111111
)
2
∗
2
(
15
−
127
)
(1.1111111)_2 * 2^{(15-127)}
(1.1111111)2∗2(15−127)=3.8368135610839464260099560574934e-34
0xbe400000= 1,0111 1100, 100 0000 0000 0000 0000=
−
(
1.1
)
2
∗
2
(
124
−
127
)
=
−
0.1875
-(1.1)_2*2^{(124-127)}=-0.1875
−(1.1)2∗2(124−127)=−0.1875
0xff800000= 1,1111 1111, 000 0000 0000 0000 0000 0000 =
−
∞
-∞
−∞ ???
补充:十六进制数中a是10 b是11 …以此类推
(2) 【双精度// 偏移度为1023】
(为什么第一个是1.0101 第二个是0.1? 因为这里的阶码是0,表示特别小的一个数。尾数前面的那个1就不能加了…浮点数表示为
0.
f
∗
2
e
−
1022
0.f \ * 2^{e-1022}
0.f ∗2e−1022,其中-1022为最小阶码)
(3)
(4)…
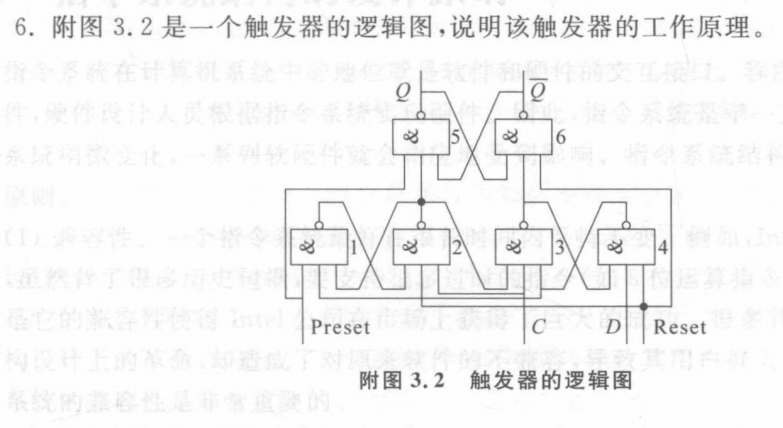
Q3: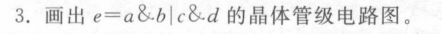
A3:

A&B|C&D=~( ~( A&B)& ~(C&D)) 两级与非门的逻辑
【模仿答案,成为答案,超越答案!】
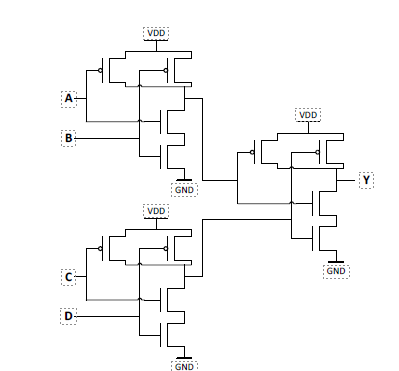
两种解法,第二种,是课本上的~(A&B|C&D)后面再加一个反相器。

A4:
FO4 定义为1 个反相器驱动 4 个相同的反相器
本征延迟:元器件固有延迟,对于反相器是指 翻转延迟
负载延迟 = 每pF延迟 ×((输入电容 + 单个负载连续电容) × 负载个数)
FO4延迟=本征延迟+负载延迟 =0.023+4.5*((0.0036+0.0044)*4)=0.167ns
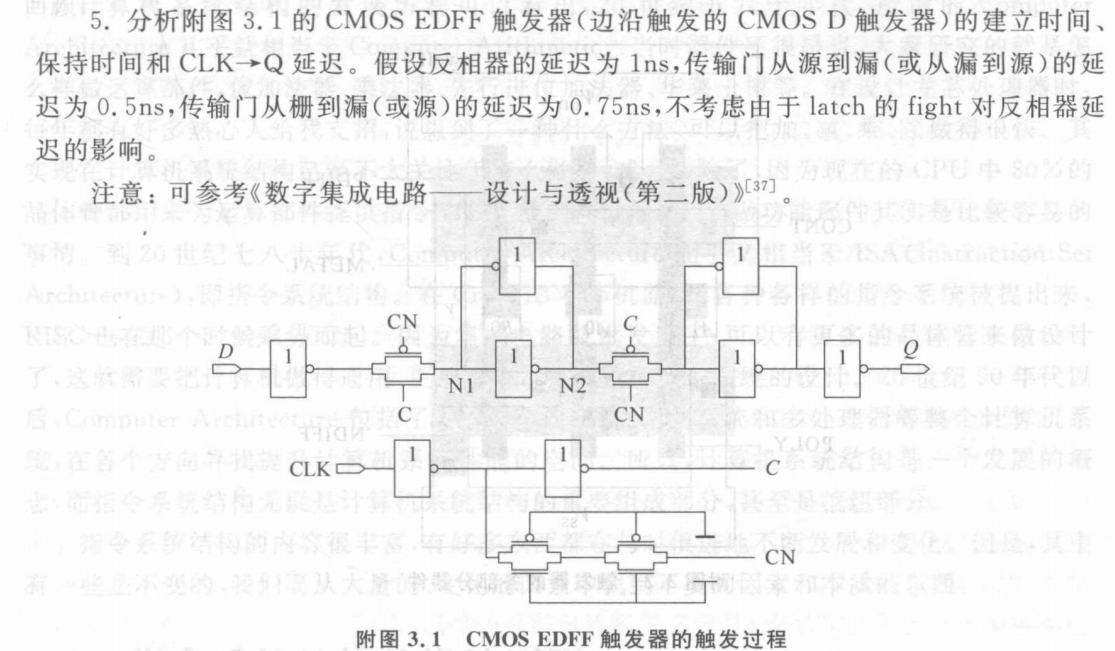
A5:
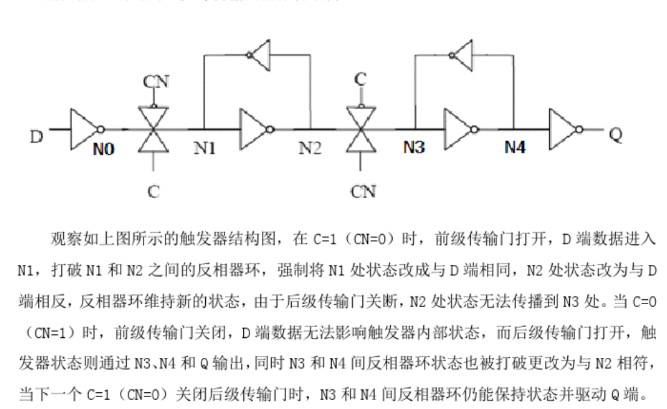
传输门
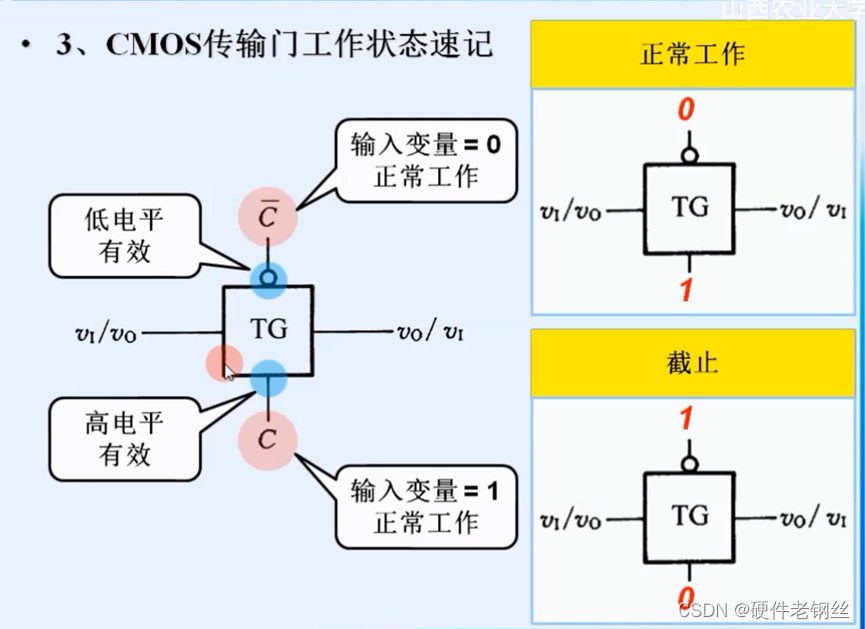
TP和TN是结构对称的器件,它们的漏极和源极是可互换的。两管的栅极由互补的信号电压(+5V和-5V)来控制,分别用C和!C表示。
setup time : 是指在时钟有效沿之前,数据输入端信号必须保持稳定的最短时间。
hold time: 是指在时钟有效沿(下图为上升沿)之后,数据输入端信号必须保持稳定的最短时间
Clk-to-q Time: 输入D满足setup/hold time要求,从时钟沿到来时刻到输出端Q变化至稳定的时间
分析: