一、前言
本题基于leetcode901股票价格趋势这道题,说一下通过java解决的一些方法。并且解释一下笔者写这道题之前的想法和一些自己遇到的错误。需要注意的是,该题最多调用 next 方法 10^4 次,一般出现该提示说明需要注意时间复杂度。
二、解决思路
①栈排序(存在超出时间限制问题)
其实笔者做这道题之前并不知道单调栈这一东西,第一时间想到的是很像之前做过的和栈相关的一道题–栈排序,毕竟都是类似按照某一顺序对栈元素进行排序。需要借用辅助栈,而考虑到它需要计算的是连续天数,不是一个简单的排序。
拿这道题给的示例输入来说:
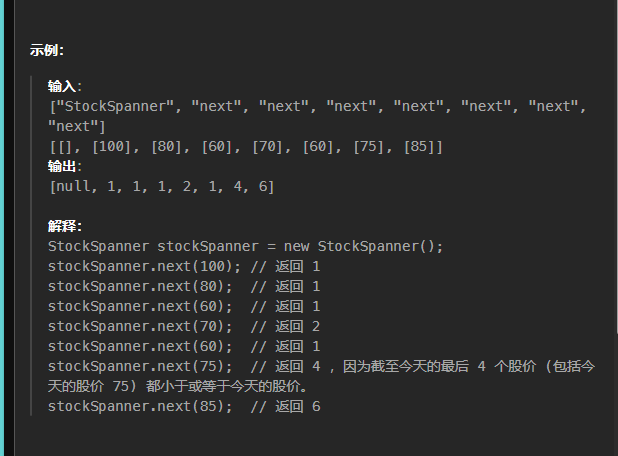
思路就是如果是空栈,那么我们直接放就好。
而当不是空栈时,此时通过price和栈顶元素的差值区分情况:
①小于0:
说明price要小,那么我们直接入栈,然后由于此时栈肯定没有比price更小的元素,所以只有它自己,return 1即可
②大于等于0:
说明此时price要大于栈顶元素,由于它要的是最大连续日数(从今天开始往回数,包括今天),那么我必须得保持入栈的一个顺序,否则就不是连续的,而是一个比当前price要小的所有天数这样一个结果。
那么怎样处理呢,我们可以先将该price入辅助栈,然后再从栈顶遍历,将小于等于当前price的栈元素弹出push到辅助栈中。此时记录辅助栈的size就是我们要返回的最大连续天数,最后再将辅助栈一次push到我们的主栈中即可。
我这边画一个图:
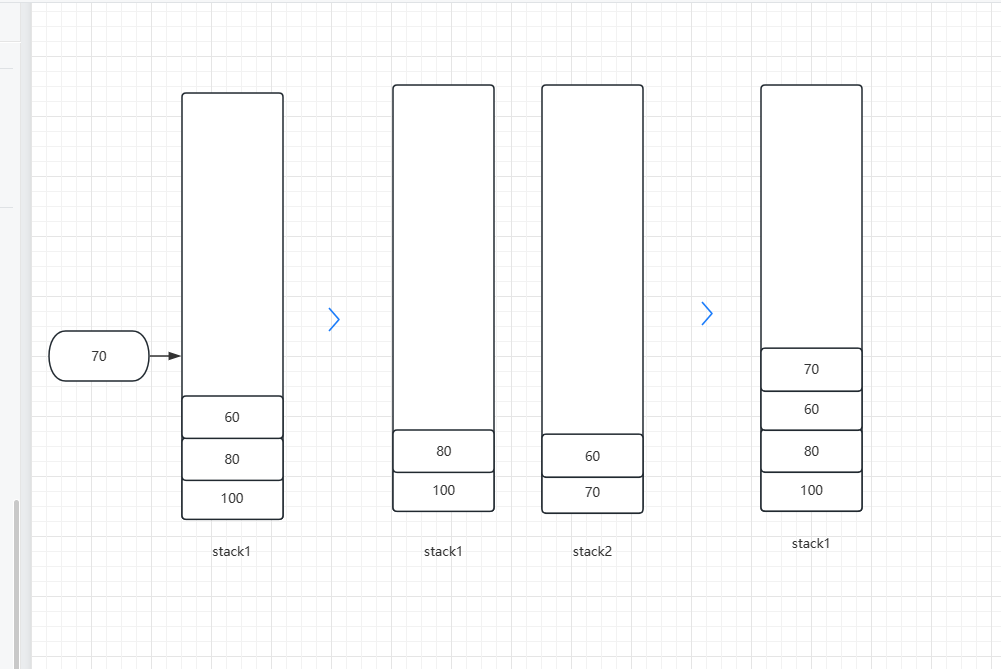
如上图,第一次入栈70这个元素时,比栈顶元素60要大,将price=70入辅助栈,然后遍历主栈栈顶,将小于等于70的元素弹出栈然后push进辅助栈,此时记录辅助栈size为2,然后将辅助栈元素全部弹出并且推入主栈,最后返回size即可。且这样不会修改我主栈元素的原本顺序,就是按照next元素的顺序进行排序的,就也顺便解决了连续这个问题。
同理,后面入75如下图所示:
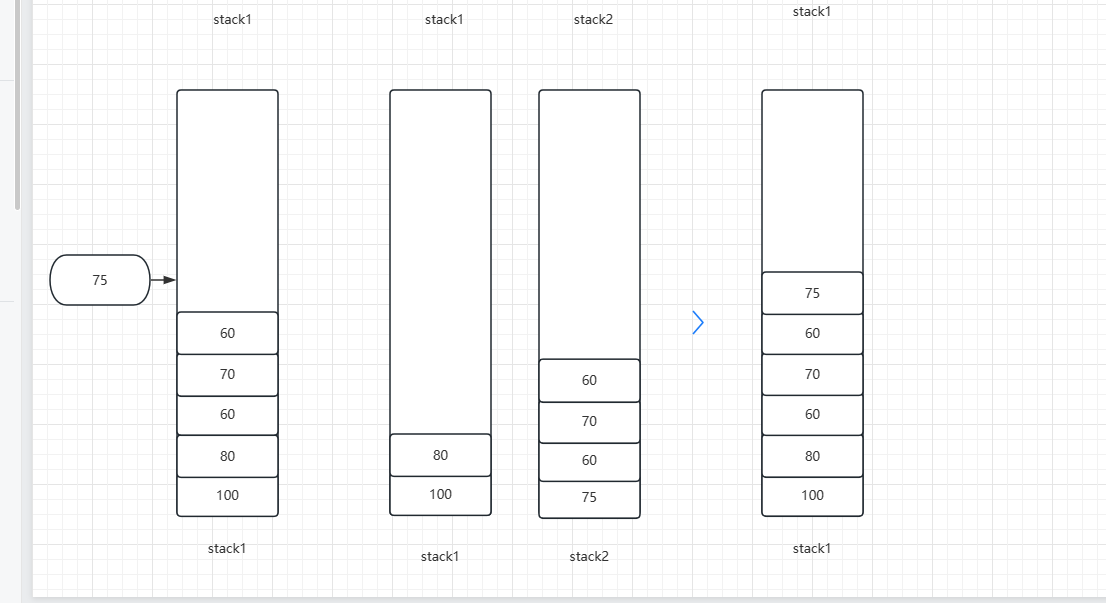
代码如下:
class StockSpanner {
private Stack<Integer> stockStack;
private Stack<Integer> diffStack;
public StockSpanner() {
stockStack = new Stack<>();
diffStack = new Stack<>();
}
public int next(int price) {
if (stockStack.isEmpty()) {
stockStack.push(price);
return 1;
} else {
int diff = price - stockStack.peek();
if (diff < 0) {
stockStack.push(price);
return 1;
} else {
diffStack.push(price);
while (!stockStack.isEmpty() && stockStack.peek() <= price) {
diffStack.push(stockStack.pop());
}
int res = diffStack.size();
while (!diffStack.isEmpty()) {
stockStack.push(diffStack.pop());
}
return res;
}
}
}
}
好像这样思路确实没什么问题,运行发现超出时间限制o(╥﹏╥)o:
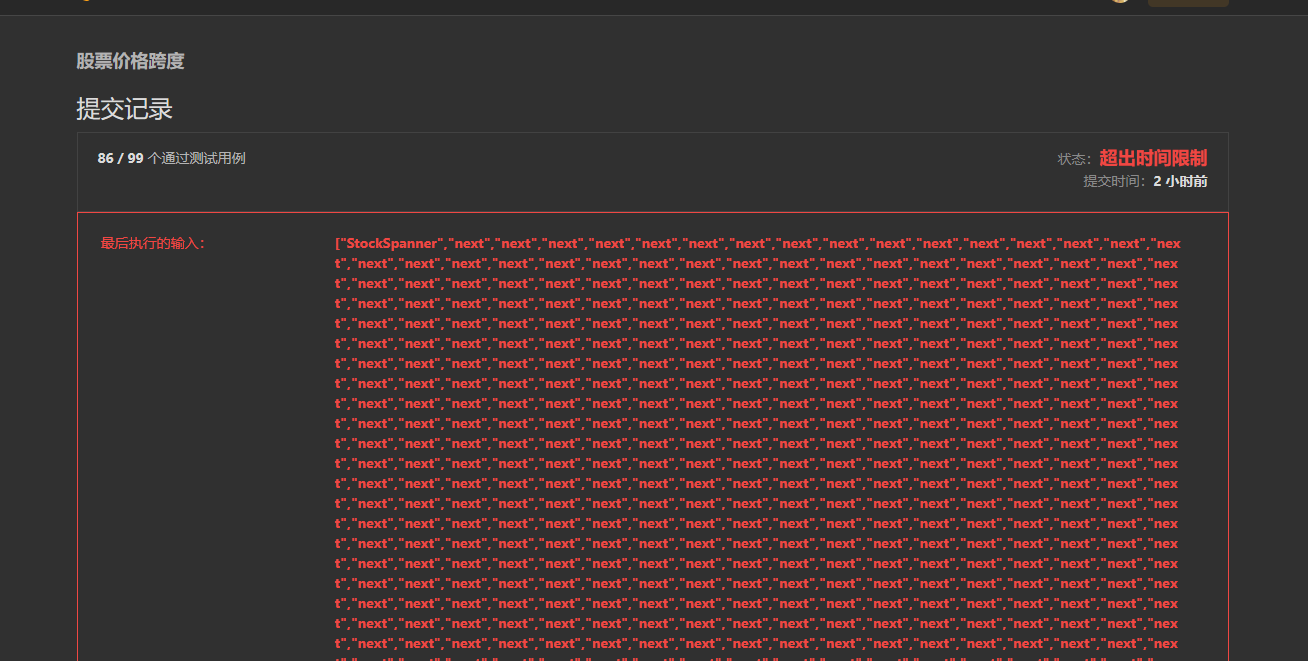
虽说时间复杂度是O(n),可是这样的操作确实还是非常繁琐的,且还需要借助辅助栈且最后主栈的元素量是Next()的调用次数,无效或者其实用不上的元素根本没有pop出栈,导致浪费了很多空间。
所以也就有了后面一种方法–单调栈,该方法不再需要辅助栈,且不会浪费额外空间。
②单调栈
我们将每一个股票价格想象成java的一个对象,它拥有它的id,拥有它的价格,我们可以使用一个int[]去承装他们,int[0]装id,int[1]装价格。
然后我们可以想象下,我们需要比今日股票要小于等于的天数,是否就是将这些对象给按照一个单调递减的顺序排序,如果放入的元素比上一个元素要小,此时结果就是当前放入元素的下标id和上一个元素下标的差值。如果要大,此时不符合单调递减,那么我需要将比它小的元素全部抹去,让我们承装对象的结构始终符合单调递减,此时结果是当前当如元素的下标id和抹去后的它的上一个元素下标id的差值。
为了方便我们后续程序少一些空栈之类的判断,我们初始化的时候可以先push进一个id为0,价格是Integer.MAX的元素,这样到时候我们出栈也不用担心会导致空栈。
而对于next方法,首先是下标,这个很好理解,我们每次调用next方法时,id++即可,很像我们数据库的ID自增策略。由于我们需要的是小于或等于今天价格的最大连续日数,所以是一个单调递减栈,如果要插入的price大于栈顶元素,此时将单调栈的元素依次弹出,并且此时将当前price对应的下标减去出栈后的栈顶元素的下标,这个下标差就是我们需要返回的结果。然后再将当前元素入栈即可然后返回下标差即可。
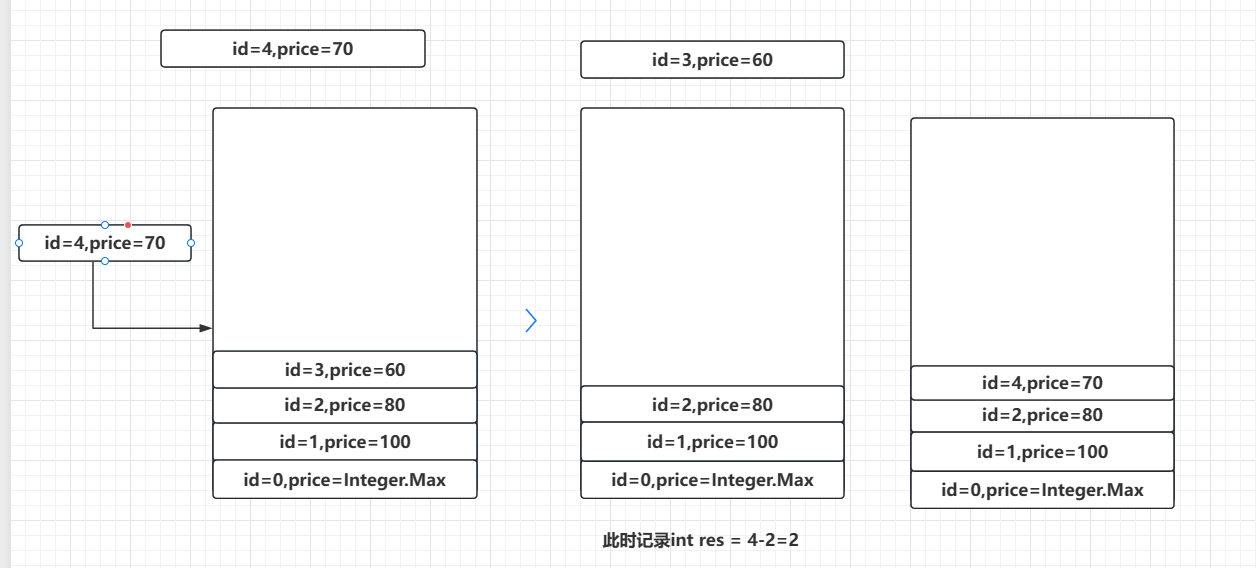
仍然拿示例1举例:
当我插入100-80-60,由于每次插入都比栈顶元素要小,而当插入70时,此时比栈顶元素60要大,从栈顶开始遍历,一直到栈顶元素大于price为止,此时出栈完后栈顶是id=2,price=80这个元素,然后记录res=4-2=2,然后将price=70,id=4这个元素入栈。
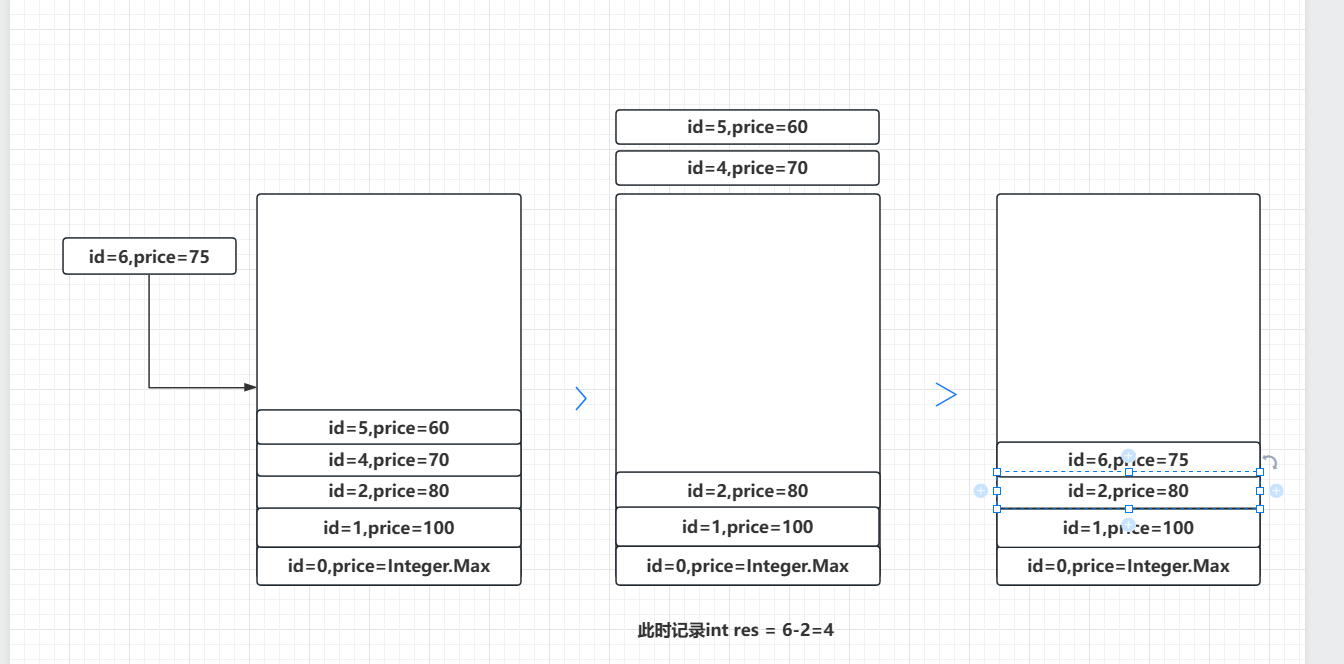
放入60,75同理:
代码如下:
class StockSpanner {
private Deque<int[]> stockStack;
private int id;
public StockSpanner() {
stockStack = new ArrayDeque<>();
stockStack.push(new int[]{0,Integer.MAX_VALUE});
id = 0;
}
public int next(int price) {
id ++;
while (price >= stockStack.peek()[1]){
stockStack.pop();
}
int ret = id - stockStack.peek()[0];
stockStack.push(new int[]{id, price});
return ret;
}
}
三、栈排序和单调栈的区别
那么其实栈排序和单调栈是有明显区别的,这里做一个总结:
单调栈:单调栈是一种特殊的栈结构,其插入时保证栈内元素的单调性。通常用于解决数组中下一个更大或下一个更小元素的问题。例如我们可以见我们力扣496下一个更大元素 I这道题,单调栈需要维护一个单调递增或单调递减的栈顶元素序列,每当新元素插入时,都需要判断该元素与栈顶元素的大小关系,不断弹出栈顶元素直到满足单调性。
栈排序:栈排序是对栈内元素进行递增或递减排序的一种思路。通常使用额外的栈来辅助排序。将原始栈的元素依次弹出,插入到辅助栈中的正确位置,最后将辅助栈中的元素重新压回原始栈中,从而实现了栈排序。需要注意的是,仅使用原始栈是无法实现栈排序的,因为栈的弹出顺序一旦改变就无法恢复。
总体来说,单调栈和栈排序都是基于栈实现的常用算法思路,但其应用场景和实现方法不同。单调栈通常用于解决比较问题,需要维护栈内元素的单调性;而栈排序则是对栈内元素的排序,需要额外借助辅助栈实现。