CCF CSP认证 历年题目自练Day23
题目一
试题编号: 202006-1
试题名称: 线性分类器
时间限制: 1.0s
内存限制: 512.0MB


题目分析(个人理解)
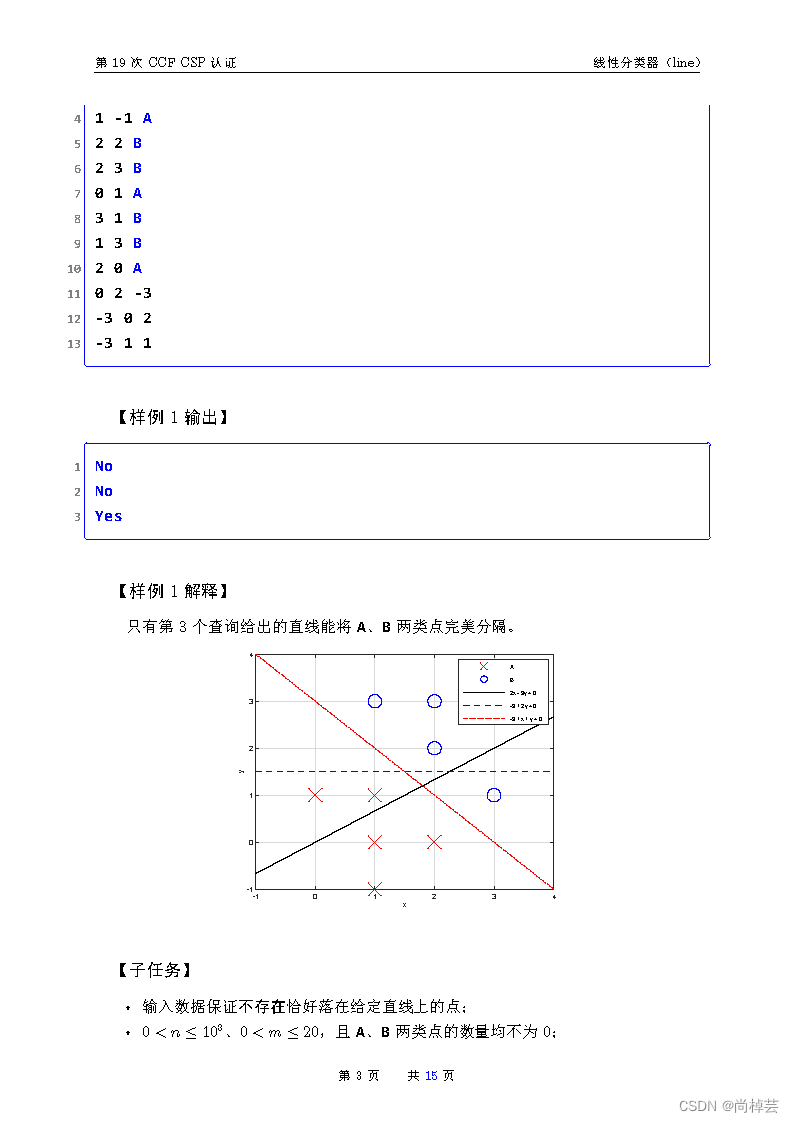
- 题目很长,专门吓唬人的,第一行输入两个数n是坐标数,m表示有几条直线,后面的每一行输入点的坐标和该点坐标属于哪一类(A或B)。点输完之后,再输入直线的三个参数,Ax+By+C=0 输入的就是A,B,C。
- ok!现在需要判断哪条直线能够将A类和B类一刀切开,也就是直线上方要不全是B类要不全是A类,下方同理。如果能够满足且开的条件那就输出yes否则就no。
- 首先,输入的坐标我选择存储在列表中,一个点(带类)存入一个列表中,然后将多个列表追加写入到s[]中,下面进入循环判断的步骤,如何判断是在直线上方还是在下方?那么就不得不分类讨论了,当C等于0时,当x<-B/A时必然在直线上方,反之在下方(用x即可判断下方还是上方)。当C不等于0时,用y判断,如果(th0+th1*x)/-th2>y则就在直线上方(初中数学,一元一次函数)。
- 在上方就把t写入shang[],在下方就把t写入xia[],最后遍历每一个shang[]和xia[]每一个元素是否有不同的,如果有不同的就输出no 否则输出yes
- 上代码!!!
n,m=map(int,input().split())
s=[]#存储坐标
for i in range(n):
x,y,t=input().split()
x,y=int(x),int(y)
s.append([x,y,t])
for i in range(m):
shang = []#位于线上方的点 th2=0时是位于线左边的点
xia = []#位于线下方的点 th2=0时是位于线右边的点
bl=True
th0,th1,th2=map(int,input().split())
if th2==0:
for x, y, t in s:
if x<th0/-th1:
shang.append(t)
else:
xia.append(t)
else:
for x,y,t in s:
if (th0+th1*x)/-th2>y:
shang.append(t)
else:
xia.append(t)
if len(shang) > 1:#仅有一个点则必不可能分类错误
for j in range(1,len(shang)):
if shang[j] != shang[j-1]:#不等,即分类错误
bl=False
break
if len(xia)>1:
for j in range(1,len(xia)):
if xia[j]!=xia[j-1] or bl==False:#加bl为减少时间复杂度
bl=False
break
if bl==False:
print("No")
else:
print("Yes")
题目二
试题编号: 202006-2
试题名称: 稀疏向量
时间限制: 2.0s
内存限制: 512.0MB


题目分析(个人理解)
- 第一种方法, 全部采用列表存储和操作,第一行输入n维度,后面输入向量v和u不为0的数有几个(我记为m1,m2)。
- 之后每一行输入不为0的数的位置和值,我们不难发现m1+m2就是向量维度不为0的个数。我将不为0的值追加写入s[]中,然后判断s[0][0]到s[m1+m2-1][0]是否有相等的,如果相等就把s[][1]*s[][1]累加到num中。最后输出即可,但是注意,此种方法逻辑没问题就是时间复杂度太大了,超时了,不行。
- 代码如下:
n,m1,m2=map(int,input().split())
num=0
s=[]
for i in range(m1+m2):
l=list(map(int,input().split()))
s.append(l)
for j in range(m1+m2-1):
for k in range(1,m1+m2):
if s[j][0]==s[k][0] and k!=j:
num+=s[j][1]*s[k][1]
print(num)
- 我只好采用字典去存储和操作,将键设置为维度,值设置为对应维度的值,然后遍历字典中的键,然后存在就相乘最后加在num中,最后输出即可!
- 上代码!!!
n,a,b=map(int,input().split())
u={}
for i in range(a):
k,e=map(int,input().split())
u[k]=e
num=0
for i in range(b):
k,e=map(int,input().split())
if k in u.keys():
num+=e*u[k]
print(num)
总结
好饿!!!!还要开班会!