简单来说,立方体贴图就是一个包含了6个2D纹理的纹理,每个2D纹理都组成了立方体的一个面:一个有纹理的立方体。你可能会奇怪,这样一个立方体有什么用途呢?为什么要把6张纹理合并到一张纹理中,而不是直接使用6个单独的纹理呢?立方体贴图有一个非常有用的特性,它可以通过一个方向向量来进行索引/采样。假设我们有一个1x1x1的单位立方体,方向向量的原点位于它的中心。使用一个橘黄色的方向向量来从立方体贴图上采样一个纹理值会像是这样:
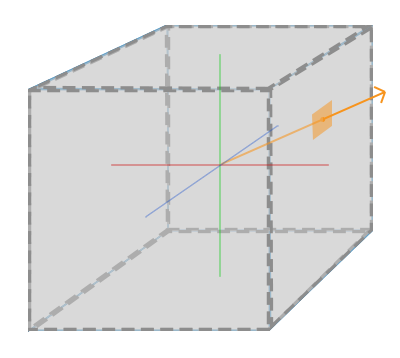
创建立方体贴图
立方体贴图是和其它纹理一样的,所以如果想创建一个立方体贴图的话,我们需要生成一个纹理,并将其绑定到纹理目标上,之后再做其它的纹理操作。这次要绑定到GL_TEXTURE_CUBE_MAP:
unsigned int textureID;
glGenTextures(1, &textureID);
glBindTexture(GL_TEXTURE_CUBE_MAP, textureID);因为立方体贴图包含有6个纹理,每个面一个,我们需要调用glTexImage2D函数6次,参数和之前教程中很类似。但这一次我们将纹理目标(target)参数设置为立方体贴图的一个特定的面,告诉OpenGL我们在对立方体贴图的哪一个面创建纹理。这就意味着我们需要对立方体贴图的每一个面都调用一次glTexImage2D。
由于我们有6个面,OpenGL给我们提供了6个特殊的纹理目标,专门对应立方体贴图的一个面。
| 纹理目标 | 方位 |
|---|---|
GL_TEXTURE_CUBE_MAP_POSITIVE_X |
右 |
GL_TEXTURE_CUBE_MAP_NEGATIVE_X |
左 |
GL_TEXTURE_CUBE_MAP_POSITIVE_Y |
上 |
GL_TEXTURE_CUBE_MAP_NEGATIVE_Y |
下 |
GL_TEXTURE_CUBE_MAP_POSITIVE_Z |
后 |
GL_TEXTURE_CUBE_MAP_NEGATIVE_Z |
前 |
和OpenGL的很多枚举(Enum)一样,它们背后的int值是线性递增的,所以如果我们有一个纹理位置的数组或者vector,我们就可以从GL_TEXTURE_CUBE_MAP_POSITIVE_X开始遍历它们,在每个迭代中对枚举值加1,遍历了整个纹理目标:
int width, height, nrChannels;
unsigned char *data;
for(unsigned int i = 0; i < textures_faces.size(); i++)
{
data = stbi_load(textures_faces[i].c_str(), &width, &height, &nrChannels, 0);
glTexImage2D(
GL_TEXTURE_CUBE_MAP_POSITIVE_X + i,
0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data
);
}这里我们有一个叫做textures_faces的vector,它包含了立方体贴图所需的所有纹理路径,并以表中的顺序排列。这将为当前绑定的立方体贴图中的每个面生成一个纹理。
因为立方体贴图和其它纹理没什么不同,我们也需要设定它的环绕和过滤方式:
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
不要被GL_TEXTURE_WRAP_R吓到,它仅仅是为纹理的R坐标设置了环绕方式,它对应的是纹理的第三个维度(和位置的z一样)。我们将环绕方式设置为GL_CLAMP_TO_EDGE,这是因为正好处于两个面之间的纹理坐标可能不能击中一个面(由于一些硬件限制),所以通过使用GL_CLAMP_TO_EDGE,OpenGL将在我们对两个面之间采样的时候,永远返回它们的边界值。
在绘制使用立方体贴图的物体之前,我们要先激活对应的纹理单元,并绑定立方体贴图,这和普通的2D纹理没什么区别。
在片段着色器中,我们使用了一个不同类型的采样器,samplerCube,我们将使用texture函数使用它进行采样,但这次我们将使用一个vec3的方向向量而不是vec2。使用立方体贴图的片段着色器会像是这样的:
in vec3 textureDir; // 代表3D纹理坐标的方向向量
uniform samplerCube cubemap; // 立方体贴图的纹理采样器
void main()
{
FragColor = texture(cubemap, textureDir);
}
看起来很棒,但为什么要用它呢?恰巧有一些很有意思的技术,使用立方体贴图来实现的话会简单多了。其中一个技术就是创建一个天空盒(Skybox)。
天空盒
天空盒是一个包含了整个场景的(大)立方体,它包含周围环境的6个图像,让玩家以为他处在一个比实际大得多的环境当中。游戏中使用天空盒的例子有群山、白云或星空。下面这张截图中展示的是星空的天空盒,它来自于『上古卷轴3』:

立方体贴图能完美满足天空盒的需求:我们有一个6面的立方体,每个面都需要一个纹理。在上面的图片中,他们使用了夜空的几张图片,让玩家产生其位于广袤宇宙中的错觉,但实际上他只是在一个小小的盒子当中。
你可以在网上找到很多像这样的天空盒资源。比如说这个网站就提供了很多天空盒。天空盒图像通常有以下的形式:

加载天空盒
因为天空盒本身就是一个立方体贴图,加载天空盒和之前加载立方体贴图时并没有什么不同。为了加载天空盒,我们将使用下面的函数,它接受一个包含6个纹理路径的vector:
unsigned int loadCubemap(vector<std::string> faces)
{
unsigned int textureID;
glGenTextures(1, &textureID);
glBindTexture(GL_TEXTURE_CUBE_MAP, textureID);
int width, height, nrChannels;
for (unsigned int i = 0; i < faces.size(); i++)
{
unsigned char *data = stbi_load(faces[i].c_str(), &width, &height, &nrChannels, 0);
if (data)
{
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i,
0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data
);
stbi_image_free(data);
}
else
{
std::cout << "Cubemap texture failed to load at path: " << faces[i] << std::endl;
stbi_image_free(data);
}
}
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
return textureID;
}函数本身应该很熟悉了。它基本就是上一部分中立方体贴图的代码,只不过合并到了一个便于管理的函数中。
之后,在调用这个函数之前,我们需要将合适的纹理路径按照立方体贴图枚举指定的顺序加载到一个vector中。
vector<std::string> faces
{
"right.jpg",
"left.jpg",
"top.jpg",
"bottom.jpg",
"front.jpg",
"back.jpg"
};
unsigned int cubemapTexture = loadCubemap(faces);
现在我们就将这个天空盒加载为一个立方体贴图了,它的id是cubemapTexture。我们可以将它绑定到一个立方体中,替换掉用了很长时间的难看的纯色背景。
显示天空盒
由于天空盒是绘制在一个立方体上的,